As explained in my earlier videos, most differential equations can't be solved explicitly which thus forces us to find different ways of estimating the solution; and one of those is in the concept of direction fields. For differential equations of the form y' = F(x, y), a direction field (or slope field) is any number of points in which the slope of the line segment near that point is plotted out. This allows us to get a general idea of the shape of the curve. Direction fields are very useful to visually see the solution of a differential equation without actually having to know the precise solution. This is a very important concept to understand so make sure to watch this video!
Watch on DTube:
Watch on BitChute: https://www.bitchute.com/video/ntzl4JYo0NY3/
Watch on BitTube: https://bit.tube/play?hash=QmajQePdqoHx32FJmQ4aoMVfghQSmsSYuA1E6S9HTo6AUq&channel=111547
Watch on YouTube: https://youtu.be/zWv1y8Xp1ac
Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIhsJtu3CqeI05b6SJkQ
View Video Notes Below!
Download These Notes: Link is in Video Description.
View These Notes as an Article: https://steemit.com/@mes
Subscribe via Email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donateReuse of My Videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight Back Against Censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord Chat Room: https://mes.fm/chatroom
Check out my Reddit and Voat Math Forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist
Watch my #AntiGravity Video Series: https://mes.fm/antigravity-playlist
Follow My #MESExperiments Video Series: https://mes.fm/experiments-playlist>
NOTE: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (If Available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
-- Try 4X+ Speed by Browser Extensions, HookTube.com, Modifying Source Code.
-- Browser Extension Recommendation: https://mes.fm/videospeed-extension- Download and Read Notes.
- Read notes on Steemit #GetOnSteem
- Watch the video in parts.
Differential Equations: Direction Fields
As mentioned in my earlier videos, unfortunately, it's impossible to solve most differential equations in the sense of obtaining an explicit formula for the solution.
But despite the absence of an explicit solution, we can still learn a lot about the solution through a graphical approach (direction fields) or a numerical approach (Euler's method).
Direction Fields
Suppose we are asked to sketch the graph of a solution of the initial-value problem:
y' = x + y
y(0) = 1
We don't know a formula for the solution, so how can we possible sketch its graph?
Let's think about what the differential equation means.
The equation y' = x + y tells us that the slope at any point (x, y) on the graph (called the solution curve) is equal to the sum of the x and y-coordinates of the point as shown in the figure below:
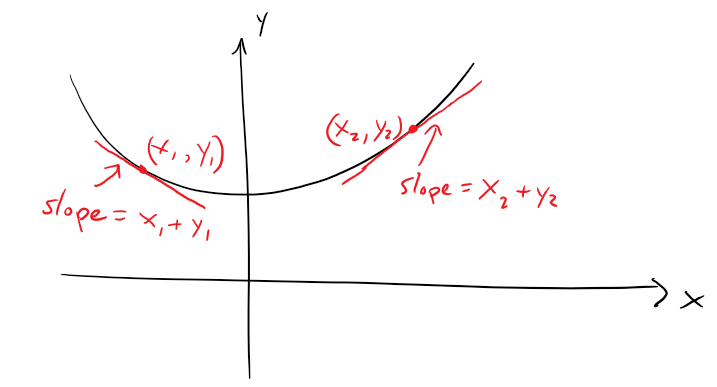
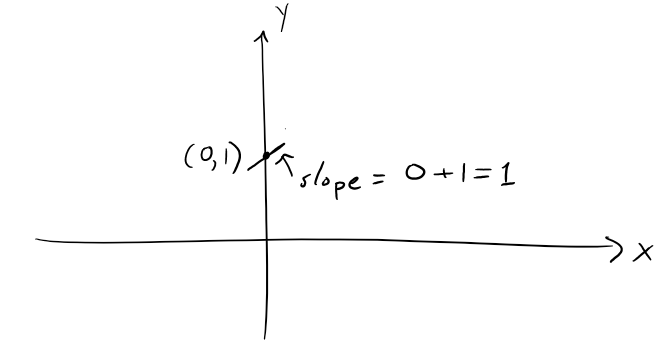
In particular, because the curve passes through the point (0, 1), i.e. our initial condition needs to be met, its slope must be 0 + 1 = 1.
So a small portion of the solution curve near the point (0, 1) looks like a short line segment through (0, 1) with slope 1 as shown in the figure below:
As a guide to sketching the rest of the curve, let's draw short line segments at a number of points (x, y) with slope x + y.
The result is called a direction field and is shown in the figure below:
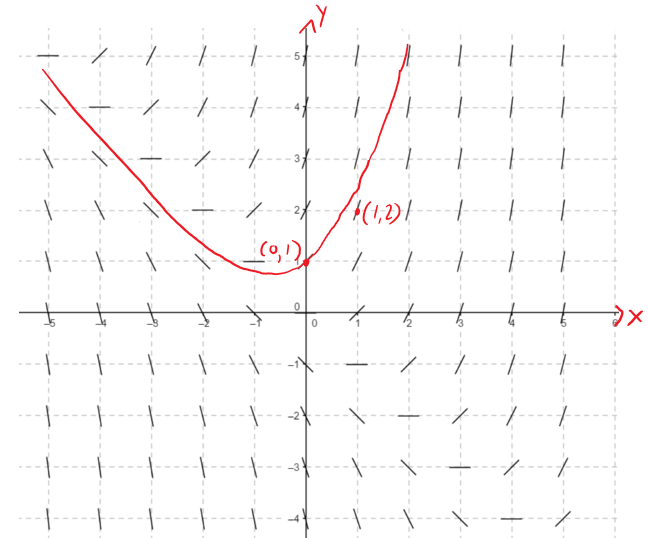
For example, the line segment at the point (1, 2) has slope 1 + 2 = 3.
The direction field allows us to visualize the general shape of the solution curves by indicating the direction in which the curves proceed at each point.
Now we can sketch the solution curve through the point (0, 1) by following the direction field.
Notice that we have drawn the curve so that it is parallel to nearby line segments.
In general, suppose we have a first-order differential equation of the form:
y' = F(x, y)
Where:
- F(x, y) is some expression in x and y.
The differential equation says that the slope of a solution curve at a point (x, y) on the curve is F(x, y).
If we draw short line segments with slope F(x, y) at several points (x, y), the result is called a direction field (or slope field).
These line segments indicate the direction in which a solution curve is heading, so the direction field helps us to visualize the general shape of these curves (even if we don't know the explicit formula for the solution).
I strongly recommend [Handbook of Differential Equations, Vol. 3][https://www.amazon.com/Handbook-Differential-Equations-Daniel-Zwillinger/dp/0127843965]. I used Vol. 2 when I did my dissertation.
You just planted 0.09 tree(s)!
Thanks to @rufusfirefly
We have planted already 6135.05 trees
out of 1,000,000
Let's save and restore Abongphen Highland Forest
in Cameroonian village Kedjom-Keku!
Plant trees with @treeplanter and get paid for it!
My Steem Power = 19029.00
Thanks a lot!
@martin.mikes coordinator of @kedjom-keku
Thank you for your contribution. Dont forget to link references and sources when applicable!
=======================================================================================
This post was upvoted and resteemed by @Steemgridcoin with the aim of promoting discussions surrounding Gridcoin and science.
This service is free. Please follow @steemgridcoin if you want to support this initiative.
Have a nice day. :)