▶️Watch on 3Speak - Odysee - BitChute - Rumble - YouTube - PDF notes
In this video I go over further into Euclidean Division and this time look at the theorem and algorithm for univariate (i.e. single-variable) polynomials. The theorem is very similar to that for integers which I covered in my earlier video, in that both cases require proving that the associated Euclidean Division Algorithm is valid to ultimately prove that the theorem is valid. The main difference between the two algorithms is that for the integer case each step involved adding 1 to the quotient; whereas for the polynomial case we need to apply a special value, s, to ensure that the degree of the remainder keeps decreasing incrementally.
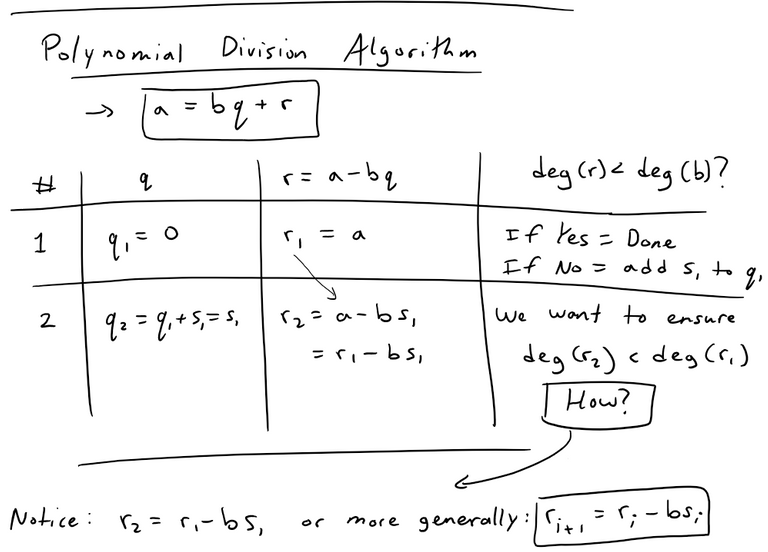
The Euclidean Theorem for Division of Polynomials is that for any two univariate polynomials a and b, where b is not equal to 0 (to avoid the case of a/0 or dividing by zero) there are associated polynomials q and r called the quotient and remainder, respectively, such that a = bq + r and the degree of r is less than the degree of b. Note also that in case the remainder is 0 and the degree of b is 0, deg(0) is defined as negative. The Division Algorithm involves starting from q = 0 and then applying the theorem formula to obtain r and checking if the degree of r is less than the degree of b. If it is, then we are done. If it is not, then we add a special polynomial s, which I show is such that involves the leading coefficients of both the remainder and the divisor, b, as well as their degrees (or number of their highest power). The selection of s is such that the remainder keeps subtracting by 1 its degree until ultimately it is less than the degree of b. Thus ultimately the algorithm is proved and thus so is the theorem!
The theorem and associated algorithm is the basis for polynomial long division where a/b = q + r/b and can be rearranged so that theorem holds true a = bq + r. This is a truly fascinating concept and make sure to walk-through both the algorithm as well as several examples to make Euclidean Division as clear as possible, so make sure to watch this video!
Polynomial Long Division Playlist
View Video Notes Below!
Become a MES Super Fan - Donate - Subscribe via email - MES merchandise
Reuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically.
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books: "Where Did the Towers Go?" by Dr. Judy Wood
Join my forums: Hive community - Reddit - Discord
Follow along my epic video series: MES Science - MES Experiments - Anti-Gravity (MES Duality) - Free Energy - PG
NOTE 1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial- Download and read video notes.
- Read notes on the Hive blockchain $HIVE
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations: Increase video speed - Increase video audio - Text to speech (Android app) – Archive webpages
Euclidean Division For Polynomials: Theorem and Proof
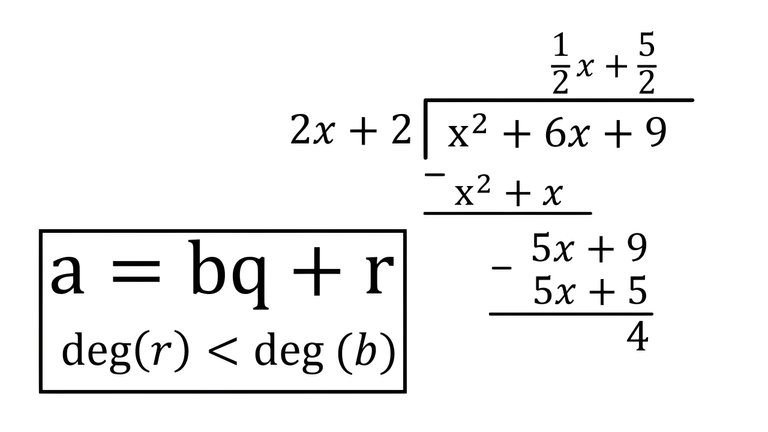
Recall from my last video on Euclidean Division for Integers:
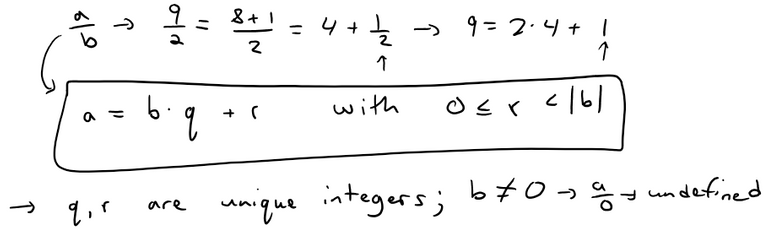
In this video I will be looking at Euclidean Division for Polynomials.
Recall that a Polynomial, more specifically a "univariate" Polynomial which consists of one variable, is of the form:
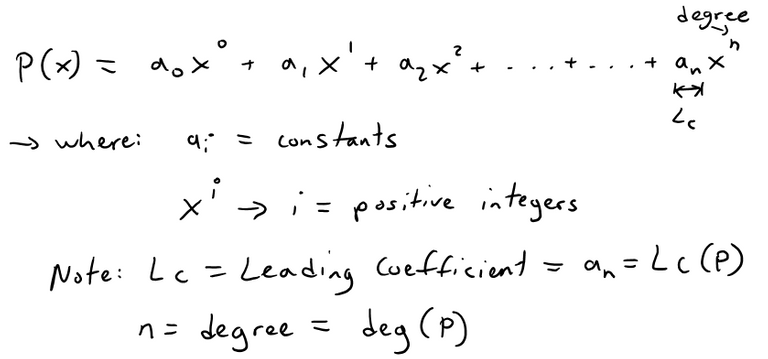
https://en.wikipedia.org/wiki/Polynomial_greatest_common_divisor#Euclidean_division
Retrieved: 20 September 2017
Archive: https://archive.is/y4IYZPolynomial greatest common divisor
…
Euclidean division
Euclidean division of polynomials, which is used in Euclid's algorithm for computing GCDs, is very similar to Euclidean division of integers. Its existence is based on the following theorem: Given two univariate polynomials a and b ≠ 0 defined over a field, there exist two polynomials q (the quotient) and r (the remainder) which satisfy
a = bq + r
and
deg(r) < deg(b),
where "deg(...)" denotes the degree and the degree of 0 is defined as negative.
Moreover, q and r are uniquely defined by these relations.
The difference from Euclidean division of the integers is that, for the integers, the degree is replaced by the absolute value, and that to have uniqueness one has to suppose that r is non-negative. The rings for which such a theorem exists are called Euclidean domains.
Like for the integers, the Euclidean division of the polynomials may be computed by the long division algorithm. This algorithm is usually presented for paper-and-pencil computation, but it works well on computers, when formalized as follows (note that the names of the variables correspond exactly to the regions of the paper sheet in a pencil-and-paper computation of long division). In the following computation "deg" stands for the degree of its argument (with the convention deg(0)<0), and "lc" stands for the leading coefficient, the coefficient of the highest degree of the variable.

The proof of the validity of this algorithm relies on the fact that during the whole "while" loop, we have a = bq + r and deg(r) is a non-negative integer that decreases at each iteration. Thus the proof of the validity of this algorithm also proves the validity of Euclidean division.
Now let's prove that the algorithm works, and hence prove Euclidean Division.
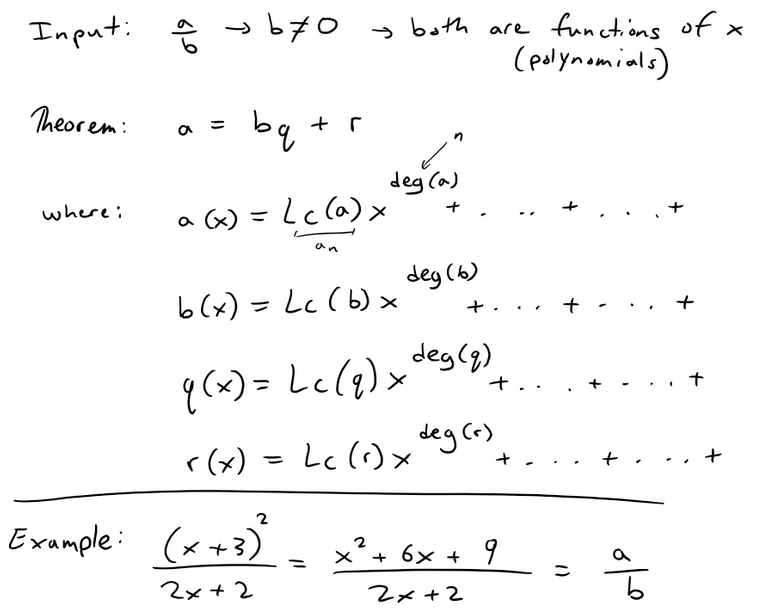
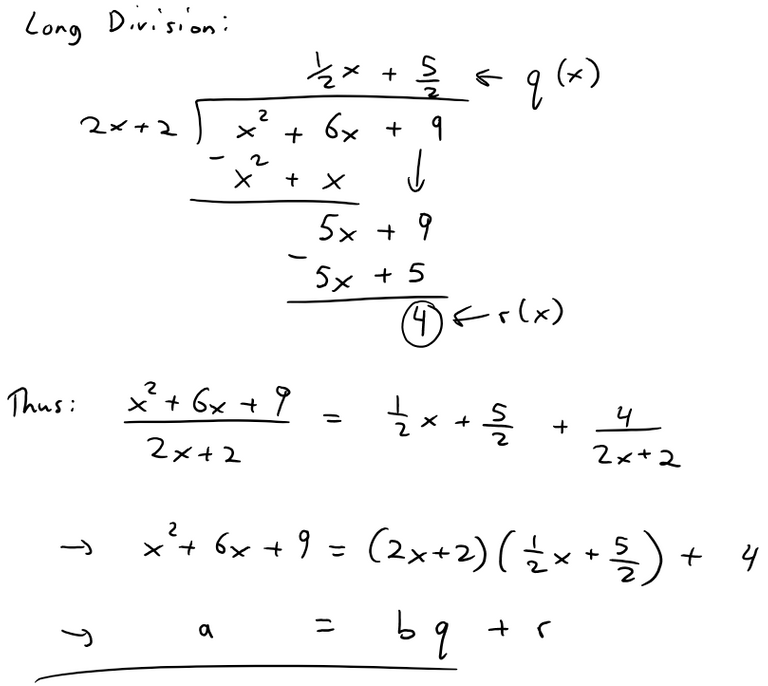
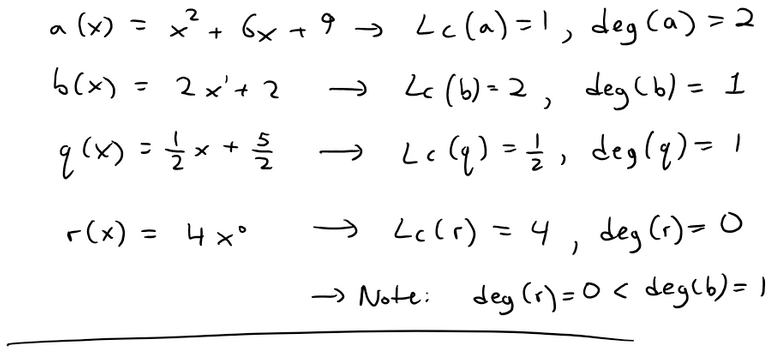
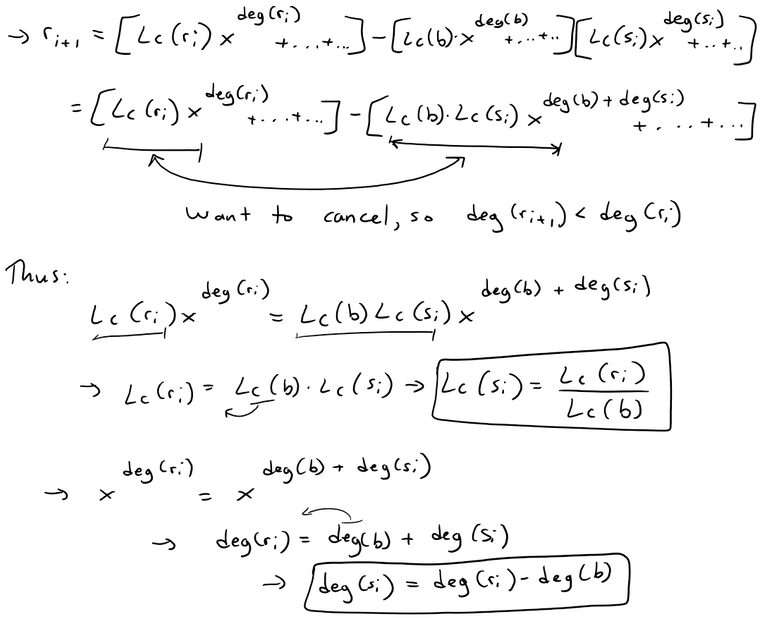


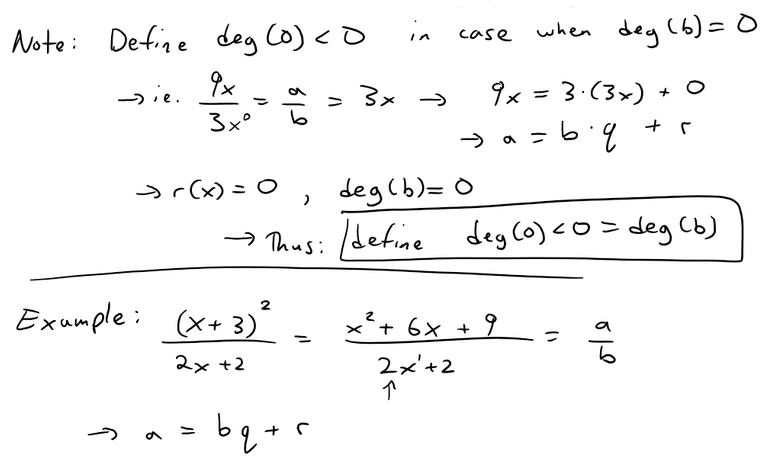
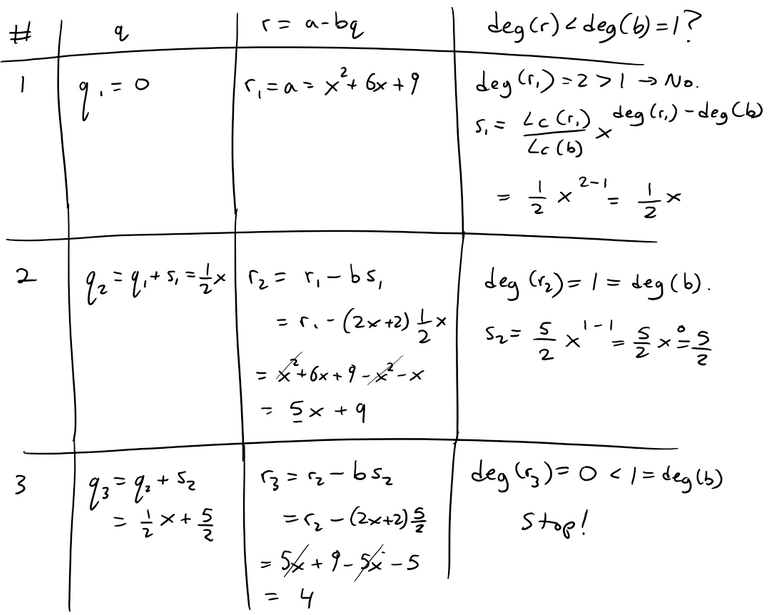

Beautiful post. Lots of work. Abstract algebra is probably one of the hardest things to learn as a math major! Keep it up!
Thanks! Yup abstract algebra requires formalizing what otherwise seems intuitive operations.
Proofs can be scary. Lol.