▶️Watch on 3Speak - Odysee - BitChute - Rumble - DTube - YouTube - PDF notes
In this video I go over Question 2 of the Laboratory Project: Taylor Polynomials and this time look at determining the accuracy of the quadratic approximation determined in Question 1. Recall from Question 1 that I showed that the quadratic or parabola approximation P(x) = 1 – (x2)/2 was much more accurate in approximating f(x) = cos(x) than a simple Linear Approximation. In this video I look at that determining the values of x in which the given accuracy is within 0.1. In other words the absolute value of the difference f(x) – cos(x) is within 0.1. To determine this I first graph the functions P(x), f(x), as well as f(x) + 0.1 and f(x) – 0.1. This allows us to visually see the region in which P(x) is accurate to within 0.1. Zooming into the intersection I show that it is equal to +/- 1.26.
Also shown in this video is a look at a numerical online solver approach to determine a more accurate value for the range. But when dealing with inequalities and numerical calculations it is important to understand that rounding up or rounding down can affect the given inequality, so always keep this in mind! This is a very useful video in understanding the accuracy associated with graphical and numerical approximations, so make sure to watch this video!
Laboratory Projects playlist
View Video Notes Below!
Become a MES Super Fan - Donate - Subscribe via email - MES merchandise
Reuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically.
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books: "Where Did the Towers Go?" by Dr. Judy Wood
Join my forums: Hive community - Reddit - Discord
Follow along my epic video series: MES Science - MES Experiments - Anti-Gravity (MES Duality) - Free Energy - PG
NOTE 1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial- Download and read video notes.
- Read notes on the Hive blockchain $HIVE
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations: Increase video speed - Increase video audio - Text to speech (Android app) – Archive webpages
Laboratory Project: Taylor Polynomials: Question 2
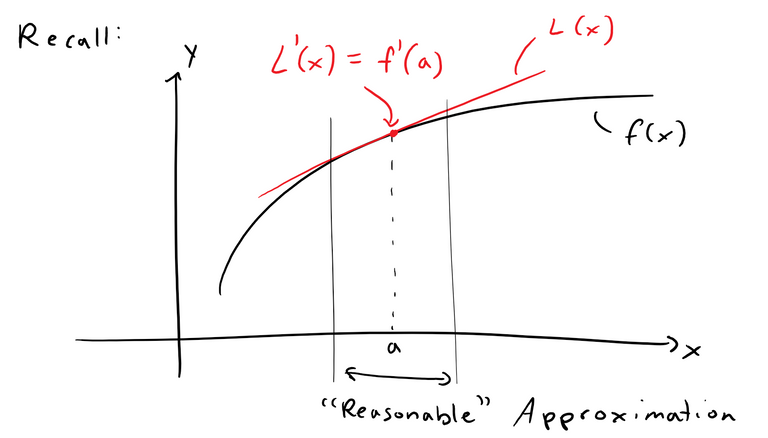
The tangent line approximation L(x) is the best first-degree (linear) approximation to f(x) near x = a because f(x) and L(x) have the same rate of change (derivative) at a.
For a better approximation than a linear one, let's try a second-degree (quadratic) approximation P(x).
In other words, we approximate a curve by a parabola instead of a straight line.
To make sure that the approximation is a good one, we stipulate the following:
i) P(a) = f(a) P and f should have the same value at a.
ii) P'(a) = f'(a) P and f should have the same rate of change at a.
iii) P"(a) = f"(a) The slopes of P and f should change at the same rate at a.
Question 1
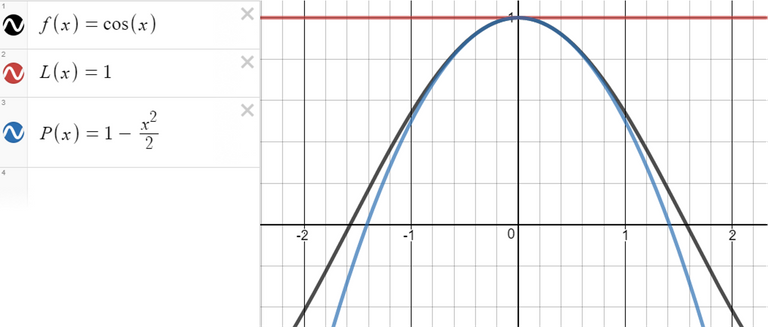
Find the quadratic approximation P(x) = A + B x + C x2 to the function f(x) = cos x that satisfies conditions i), ii), and iii) with a = 0.
Graph P, f and the linear approximation L(x) = 1 on a common screen.
Comment on how well the functions P and L approximate f.
Solution to Question 1:
https://www.desmos.com/calculator/qjplykp3pp
Retrieved: 14 October 2017
Archive: Not Available
Question 2
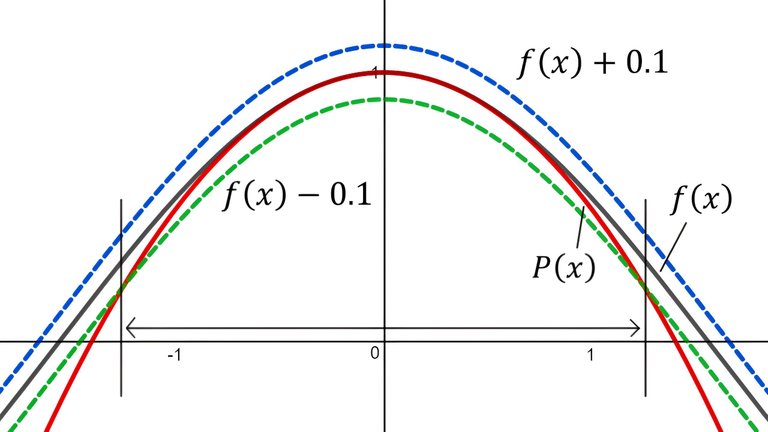
Determine the values of x for which the quadratic approximation f(x) = P(x) in Problem 1 is accurate to within 0.1. Hint: Graph y = P(x), y = cos x - 0.1, and y = cos x + 0.1 on a common screen.
Solution:
Accuracy to within 0.1 means that:
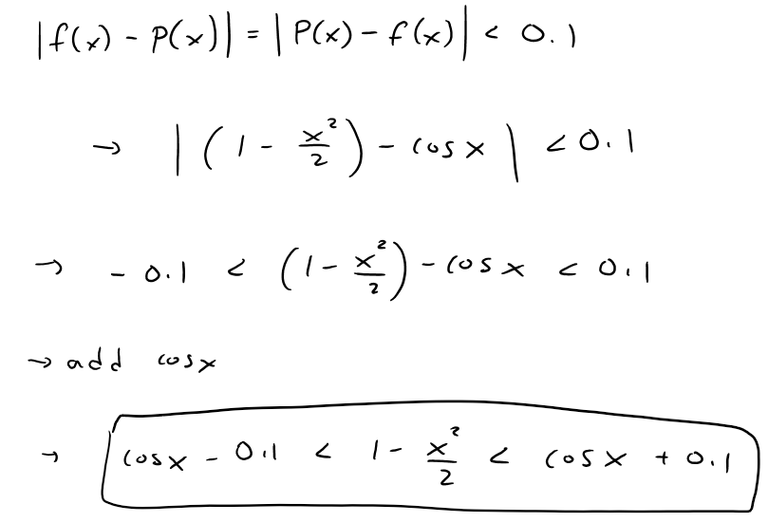
https://www.desmos.com/calculator/x09qfry3wl
Retrieved: 14 October 2017
Archive: Not Available
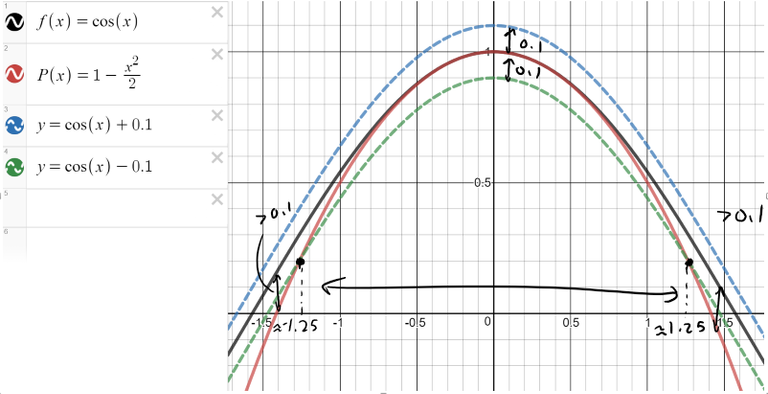
From the figure we can see the region in which P(x) is accurate to within 0.1.
It appears that this region is between -1.25 < x < 1.25.
Let's Zoom in Further!

Actually when we zoom in the intersection point appears to be about x = +/- 1.26.
Note: We include the negative because the functions are symmetric about the y-axis.
Thus, the approximation cos x ≈ 1 - x2/2 is accurate to within 0.1 within -1.26 < x < 1.26.
Note: It is not easy to solve for the x values directly because we would have to solve the following calculation at the intersection point of the above figure:
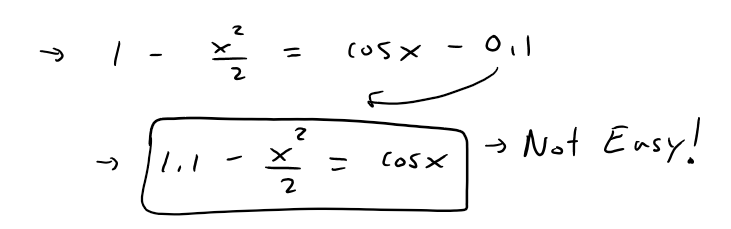
Let's solve it using an online numerical solver!
https://www.wolframalpha.com/input/?i=1-(x%5E2)%2F2%3Dcos(x)-0.1
Retrieved: 15 October 2017
Archive: Not Available
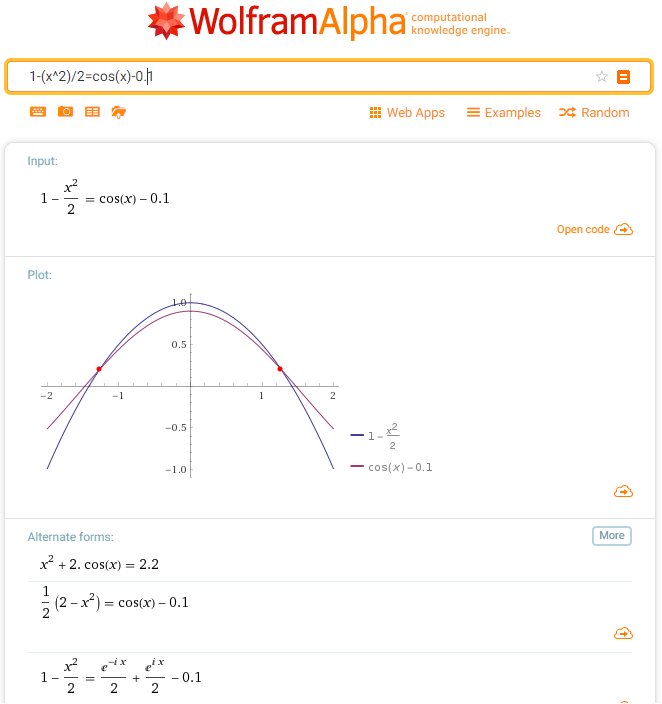
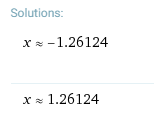
Our x = +/- 1.26 estimation was pretty close!
Thus the domain for x in which P(x) is accurate to f(x) within 0.1 is -1.2612 < x < 1.2612.
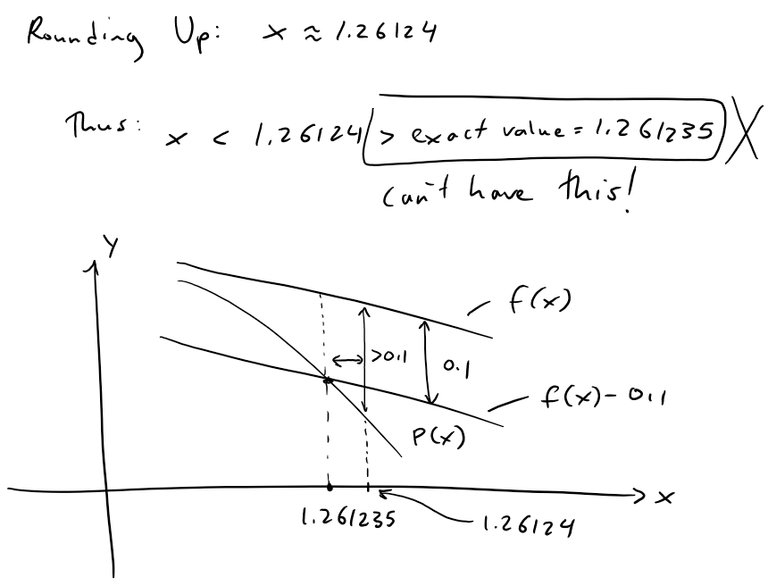
TECHNICAL NOTE: I am not sure whether Wolfram rounds up or down so to be safe I have removed the last digit in their solved x values.
If they round down than we can include the last digit because this would still ensure that |x| is less than the exact solution value.
For example, let's assume that the exact value is x = 1.261245.
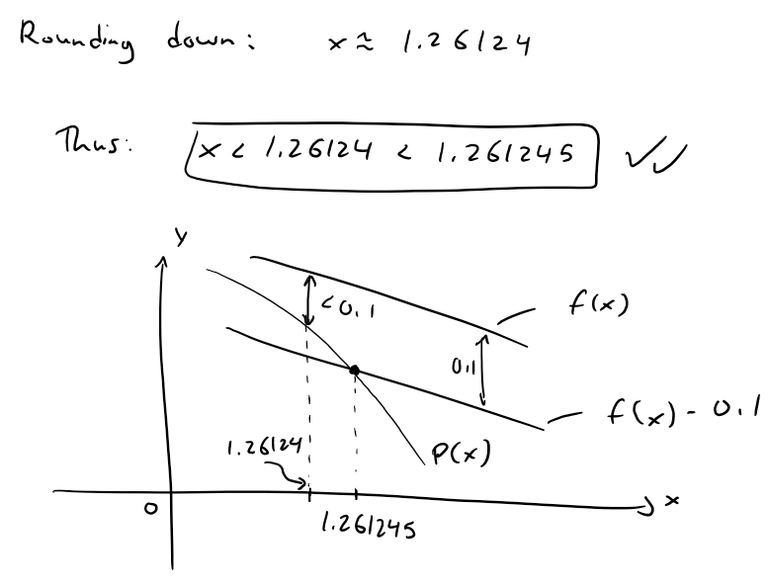
If they rounded up than technically there are values of |x| that are LARGER than the exact value, which means that for those values |P(x) - f(x)| > 0.1, which we can't have!
For example, let's assume that the exact value is x = 1.261235.