In this video I go over an example graphing parametric equations x = t2 - 2t and y = t + 1. Plotting several points from these equations shows a shape that looks like a parabola, but we can in fact confirm this is actually this case. If we eliminate the t variable from both x and y functions we do in fact get a parabola that opens up horizontally.
Also in this video I show that sometimes we restrict the t variable to be within a given interval, in which the resulting curve has a initial point, (f(a), g(a)), and a terminal point, (f(b), g(b)). Overall this is a very interesting and useful video to show how common functions such as the parabola can be written in parametric equation form; so make sure to watch this video!
Watch on DTube:
Watch on BitChute: https://www.bitchute.com/video/Qrpbl5ZD7qCx/
Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIht5QH8nHZYJM2c58gA
Download
Excel File: https://1drv.ms/x/s!As32ynv0LoaIht5Swy5SMPkigEKCYw
View Video Notes Below!
Download These Notes: Link is in Video Description.
View These Notes as an Article: https://steemit.com/@mes
Subscribe via Email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donateReuse of My Videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight Back Against Censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord Chat Room: https://mes.fm/chatroom
Check out my Reddit and Voat Math Forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Watch my #AntiGravity Video Series: https://mes.fm/antigravity-playlist
Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist
NOTE: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions
- Play this video at a faster speed.
--TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
--Try 4X+ Speed by Browser Extensions, HookTube.com, Modifying Source Code.
--Browser Extension Recommendation: https://mes.fm/videospeed-extension- Download and Read Notes.
- Read notes on Steemit #GetOnSteem
- Watch the video in parts.
Example:
Sketch and identify the curve defined by the parametric equations:
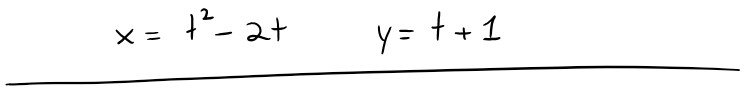
Solution:
Each value of t gives a point on the curve, as shown in the table and curve below:

A particle whose position is given by the parametric equations moves along the curve in the direction of the arrows as t increases.
Notice that at consecutive points marked on the curve appear at equal time intervals but not at equal distances.
That is because the particle slows down and then speeds up as t increases.
It appears that the curve maybe be a parabola.
This can be confirmed by eliminating the parameter t as follows:
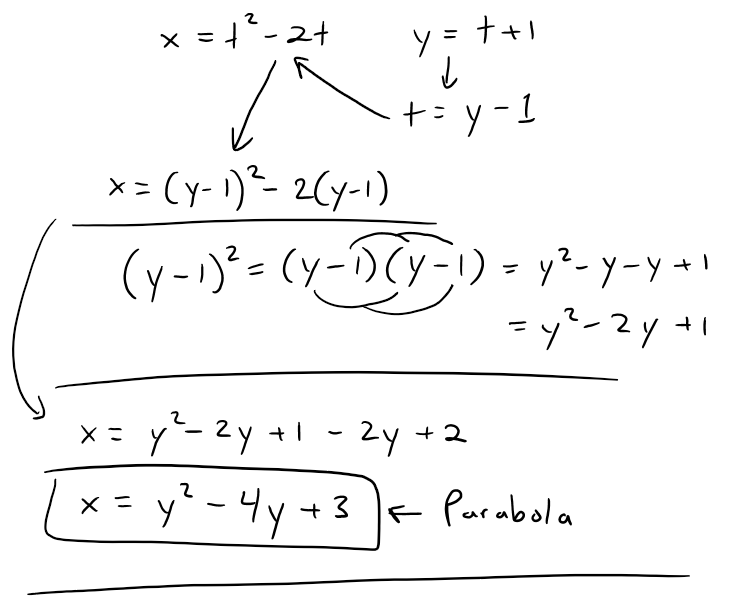
Note that no restriction was placed on the parameter t in this example, so we assumed that t could by any real number.
But sometimes we restrict t to lie in a finite interval.
For instance, consider the parametric curve:

This curve is part of the parabola that starts at (0, 1) and ends at the point (8, 5).
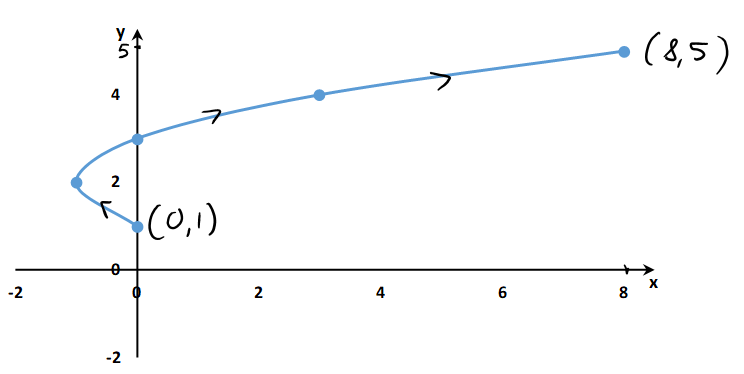
The arrowhead indicates the direction in which the curve is traced as t increases from 0 to 4.
In general, the curve with parametric equations:

O my god .. I haven't thought that parabola would also be so complex ...it is extremely out of my level.,😔😔
Curves? Is this even solvable my friend? Hihi.........