▶️Watch on 3Speak - Odysee - BitChute - Rumble - DTube - YouTube - PDF notes
In this video I go over Slant Asymptotes as well as the special case of finding Slant Asymptotes of Rational Functions through Polynomial Long Division. I actually briefly covered Slant asymptotes in my earlier video, so please ignore my statement in the video in which I said I should have covered this a long time ago, nonetheless I didn’t actually prove the special case in my earlier video. A slant asymptote is just that, an asymptote that is slanted, which is to say neither vertical nor horizontal. In other words a slanted asymptote is a linear function, and a function is said to have an slanted asymptote if it approaches the slanted line as x approaches positive or negative infinity. We can write this mathematically as the limit as x approaches infinity of the DIFFERENCE between the function and a linear function is equal to 0; i.e. the function is approaching the same value of the linear function.
The special case for slant asymptotes occurs for Rational Functions in which the degree (or highest power) of the numerator is ONE MORE than the degree of the denominator. Recall that a rational function is a division of two polynomials on the domain that the denominator is not equal to zero. Thus when we use polynomial long division to divide out these two polynomials, I show that we end up with a quotient that is in fact a linear function, i.e. has a degree of 1. And combined with the fact that the remainder has a degree less than the divisor or denominator, as shown by Euclidean Division for Polynomials, then the difference between the function and the linear quotient is simply equal to the remainder divided by the denominator. Now the limit of the latter, as I show in the video, is equal to 0 because the higher power denominator approaches infinity “faster” than the remainder thus obtaining a 1 divided by infinity scenario, i.e. approaches 0. And this proves the special case and the quotient is the linear function which is the slant asymptote.
This is a very detailed video into slant asymptotes, especially the derivation of the special case, so make sure to watch this video!
View Video Notes Below!
Become a MES Super Fan - Donate - Subscribe via email - MES merchandise
Reuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically.
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books: "Where Did the Towers Go?" by Dr. Judy Wood
Join my forums: Hive community - Reddit - Discord
Follow along my epic video series: MES Science - MES Experiments - Anti-Gravity (MES Duality) - Free Energy - PG
NOTE 1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial- Download and read video notes.
- Read notes on the Hive blockchain $HIVE
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations: Increase video speed - Increase video audio - Text to speech (Android app) – Archive webpages
Slant Asymptotes
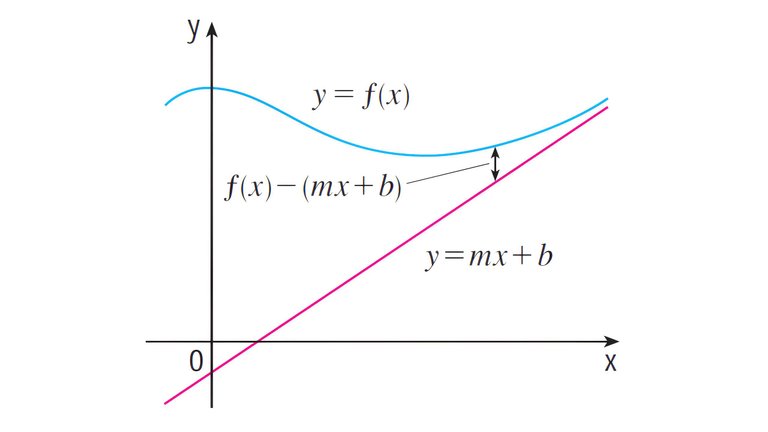
MES Note: This was a topic I should have covered a long time ago!
Some curves have asymptotes that are oblique, that is, neither horizontal nor vertical.
https://duckduckgo.com/?q=define%3Aoblique&atb=v90-1__&ia=definition
Retrieved: 13 November 2017
Archive: https://archive.is/BQ0L1

If:
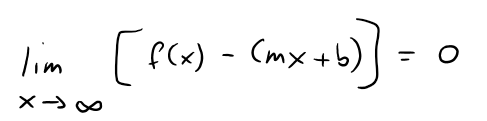
Then the line y = mx + b is called a slant asymptote because the vertical distance between the curve y = f(x) and the line y = mx + b approaches 0, as shown below.

A similar situation exists if we let x approach negative infinity.
Let's take a look at a special case:
For rational functions, slant asymptotes occur when the degree of the numerator is one more than the degree of the denominator.
In such a case the equation of the slant asymptote can be found by long division.
To see why this is the case, first recall the definition of a rational function.
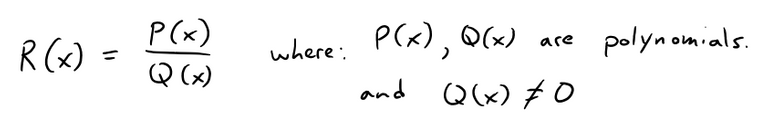
Also recall Euclidean Division for Polynomials:
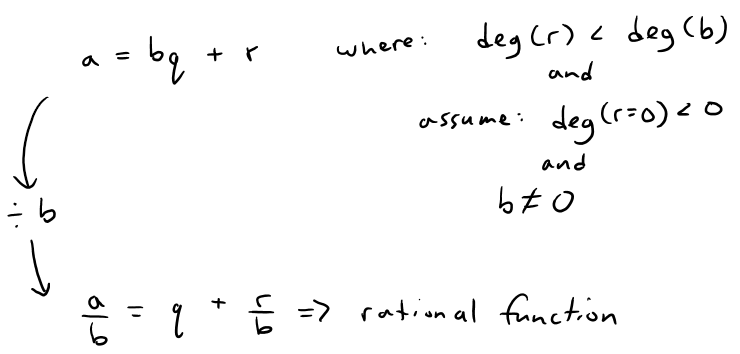
Thus if we let f(x) be a rational function with numerator P(x) and denominator Q(x), as well as the degree of the numerator being one more than the degree of the denominator, we then have:
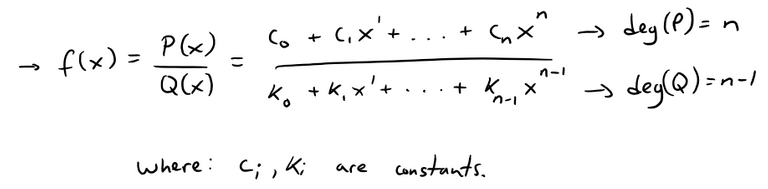
Using Polynomial Long Division, we can see that the quotient q(x) has a degree of 1, i.e. it's a linear function!
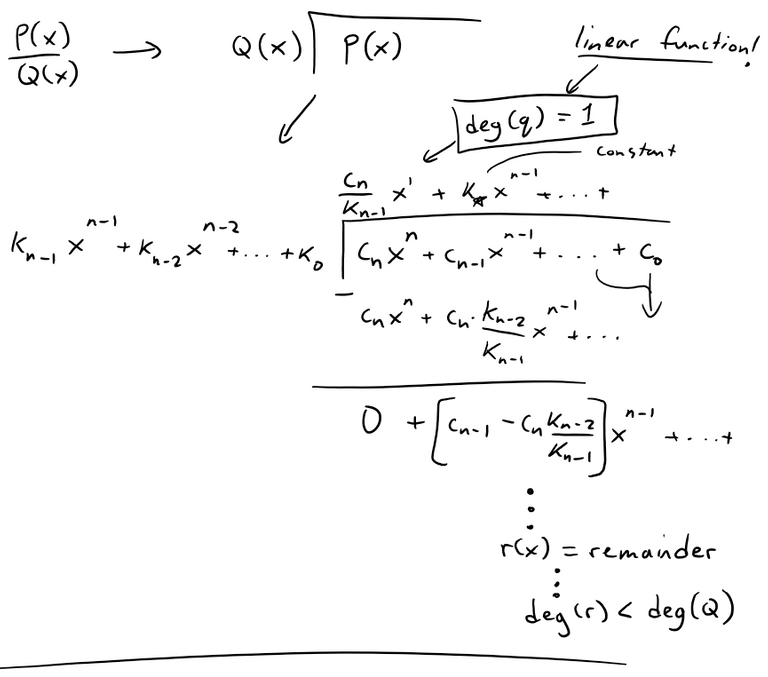

Since the degree of the remainder r is less than the degree of the divisor Q, the limit approaches 0.
To see this, consider the following:

Note: For the case where the divisor Q(x) has a degree of 0, i.e. it is a constant, then we don't have an asymptote line but rather the function f(x) itself IS the asymptote line.
