Recordemos que la función potencia se define como función polinómica de grado n, esto es: f(x)= xn donde an=1, y n es cualquier número real; siendo .gif)
, el conjunto de los números reales, su dominio.
Es importante destacar que por ser la función potencia f(x)=xn un caso particular de la función polinómica su gráfica es una curva continua cuya forma depende del valor de n en el sistema de coordenadas cartesianas.
Por ejemplo:
Cuando n=0
La función potencia se reduce a función constante f(x)=1, un caso particular de la función lineal; recordemos que la gráfica de la función constante es una recta horizontal, y que su derivada es 0. Ver.
Cuando n=1
La función potencia se reduce a función identidad f(x)=x, un caso particular de la función lineal; recordemos que la gráfica de la función identidad es una recta que pasa por el origen del sistema de coordenadas cartesianas, y que su derivada es 1. Ver.
Pasemos ahora al caso donde n=2
Cuando n=2, la función potencia es f(x)=x2, su gráfica consiste en una parábola con vértice en el origen que abre hacia arriba ocupando el I y II cuadrante en el sistema de ejes coordenados.
Veamos su gráfica con la ayuda de Desmos Calculadora Gráfica
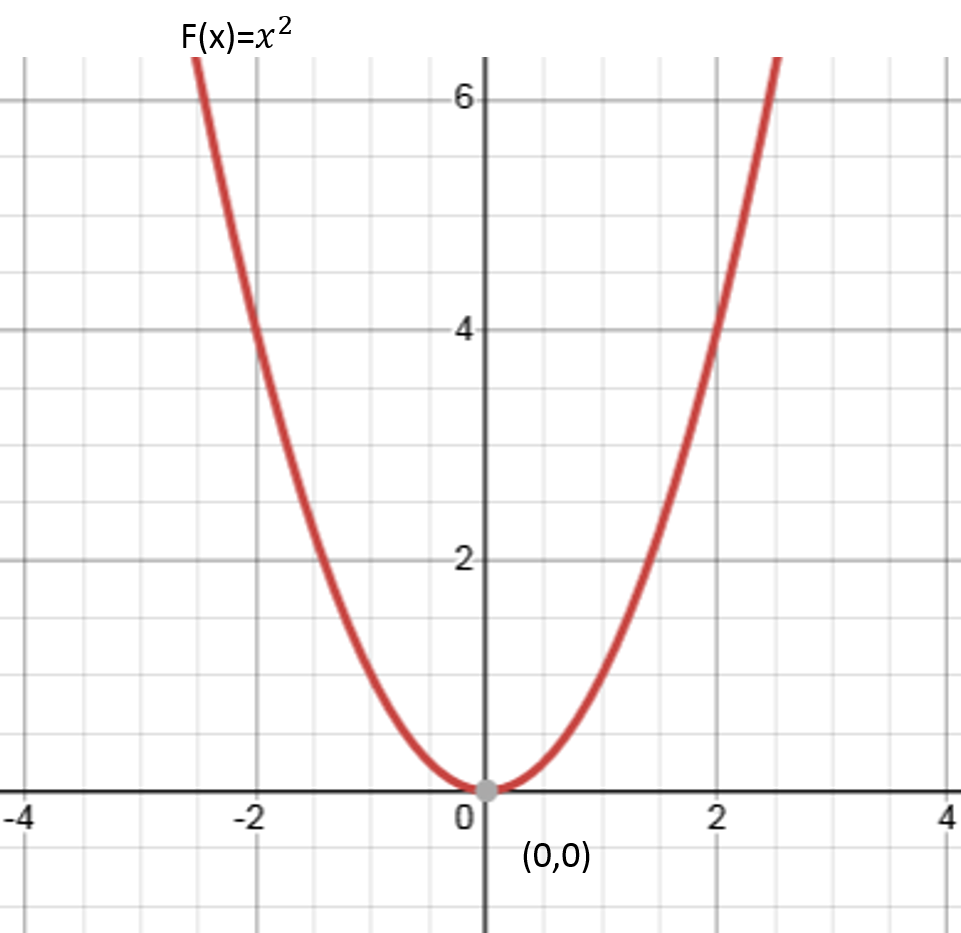
Recordemos de acuerdo a La interpretación Geométrica de la Derivada que la derivada de una función en un punto dado viene siendo la pendiente de la recta tangente al gráfico de esa función en ese punto.
Esto es:
.gif)
De lo anterior se deduce que la derivada de la función f(x)=x2 en cualquier punto x0 de su dominio viene dada por:
.gif)
De acuerdo a la definición de nuestra función f(x)=x2, para todo x en su dominio, se concluye que:
.gif)
De donde:
.gif)
Resolviendo el límite nos queda:
.gif)
Luego la derivada de f(x0)=x02 es f´(x0)=2x0
Por ejemplo, si queremos obtener la derivada de esta función en el punto x0=5 Diremos f´(5)=2.5=10
Generalicemos, ahora, para cualquier valor x0=x, y escribamos:
Si f(x)= x2 entonces f´(x)=2x
Nota: En resultado anterior, la pendiente de la recta tangente al gráfico de f(x)=x2 en el punto x=5 es 10.
Continuemos:
Cuando n=3
La función potencia queda reducida a f(x)=x3 cuya gráfica consiste en una parábola cúbica con vértice en el origen.
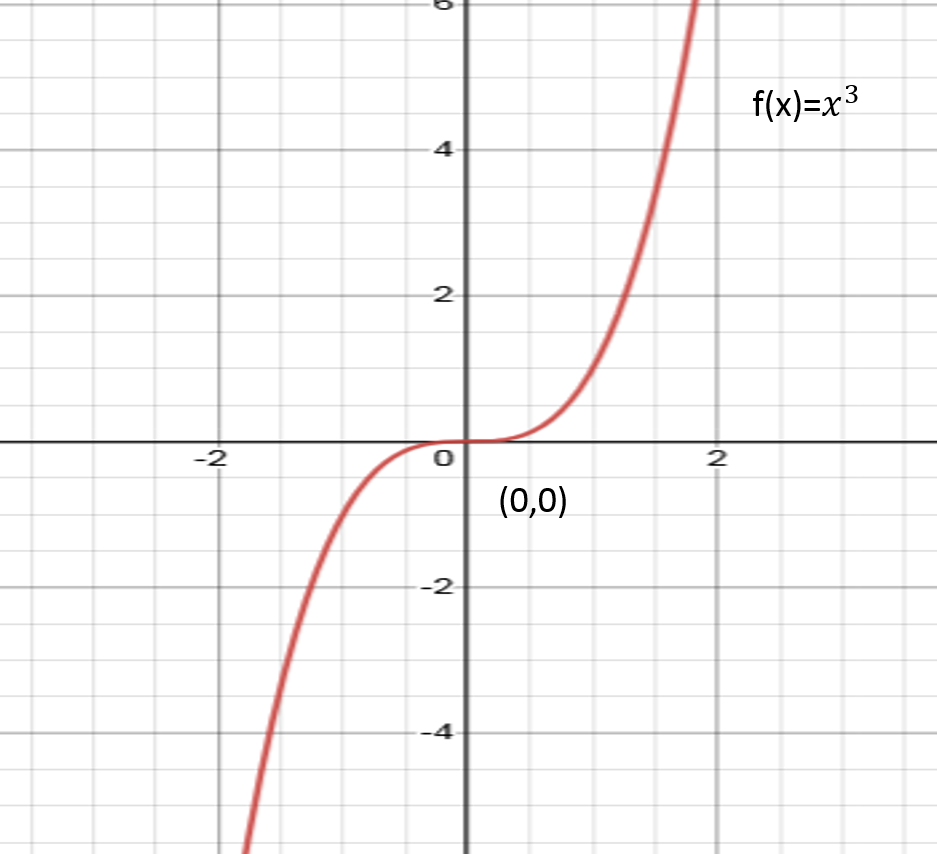
Para obtener el resultado se procede de manera similar al anterior, es decir, aplicando la definición de derivada.
.gif)
.gif)
Luego
.gif)
, y generalizando para todo x en el dominio de esta función se concluye que:
Si f(x)=x3 entonces f´(x)= 3x2
Podríamos seguir desarollando para cuando n=4, pero eso lo dejamos al lector; lo que sí podemos asegurar es que si: f(x)=x4 entonces f´(x)=4x3
En este proceso vamos descubriendo la regla para derivar a f(x)=xn. Estamos casi seguros ue ya la han descubierto.
La derivada de la función f(x)=xn potencia es f´(x)=nxn-1
Si esta regla es veraz entonces deberá ser valida para todas las funciones que hemos estudiado.
Comencemos a verificar:
Función Constante:
f(x)=x0 entonces f´(x)=0x0-1 =0x-1 =0
Función Identidad:
f(x)=x1 entonces f´(x)=1x1-1 =x0=1
Para n=2
f(x)=x2 entonces f´(x)=2x2-1=2 x1 =2x
Para n=3 f(x)=x3 entonces f´(x)=3x3-1=3x2
Pruébelo usted para n=4
Otros ejemplos
Hallar la derivada de las siguientes funciones:
.gif)
.gif)
Dejo planteado el siguiente ejercicio
.gif)
Créditos
Usamos el Editor de Ecuaciones LaTeX para editar las ecuaciones.
Desmos Calculadora Gráfica para editar las gráficas.
El contenido es totalmente original.
Su post ha sido valorado por @ramonycajal