Hi there. In this mathematics post, I cover a quick method for determining the vertex of a quadratic function. This is suitable for upper year high schools math students.

The Quadratic Function
The quadratic function is an order two polynomial function of the form:

where a is the coefficient for x-squared, b is the coefficient for x and c is the y-intercept (when x = 0).
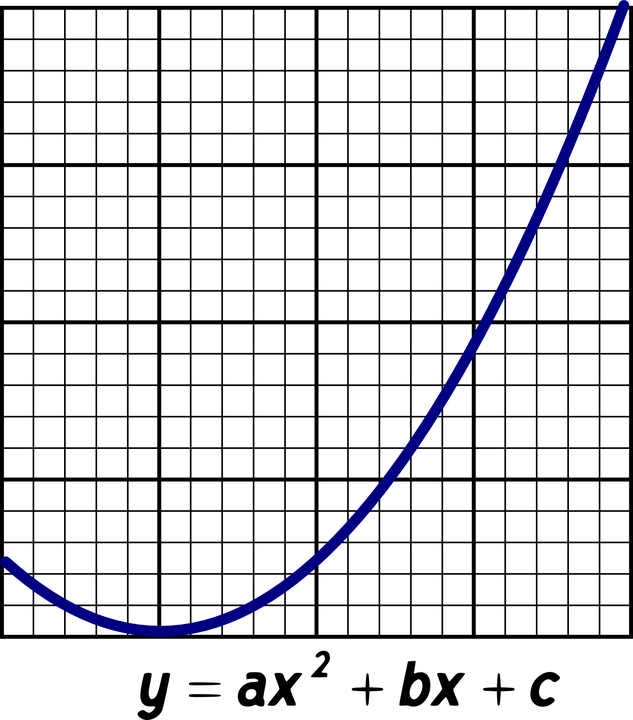
Given that a is positive, as x increases the value of y increases. Likewise when a is negative, the value of y decreases as x increases. Do keep in mind that the increase for y is not constant. This means that the increase in y is not always the same for each 1 unit of x increasing. Do refer to the next section for some visual examples of the parabola shapes from the quadratic functions.
Vertex For The Parabola
The vertex for a parabola refers the minimum or the maximum point for the quadratic function. If the coefficient value of a is positive then the parabola has a vertex point that is a minimum. Think of a positive smile for this case. When the coefficient value of a is negative, the parabola has a vertex that is a maximum. The shape of the parabola is a frown.
Here are some screenshot examples. I used the Desmos website for the graphs.
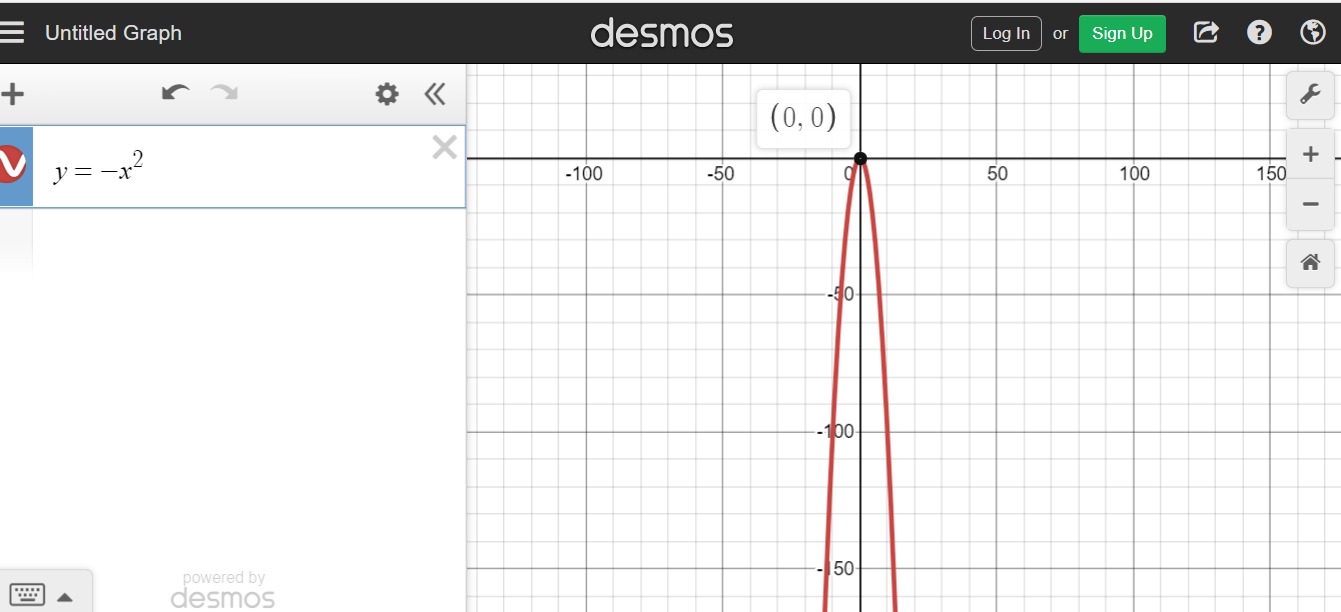
Screenshot One: y = x^2 With A Vertex/Min of (0, 0), Opens Up
Screenshot Two: y = -x^2 With A Vertex/Max of (0, 0), Opens Down
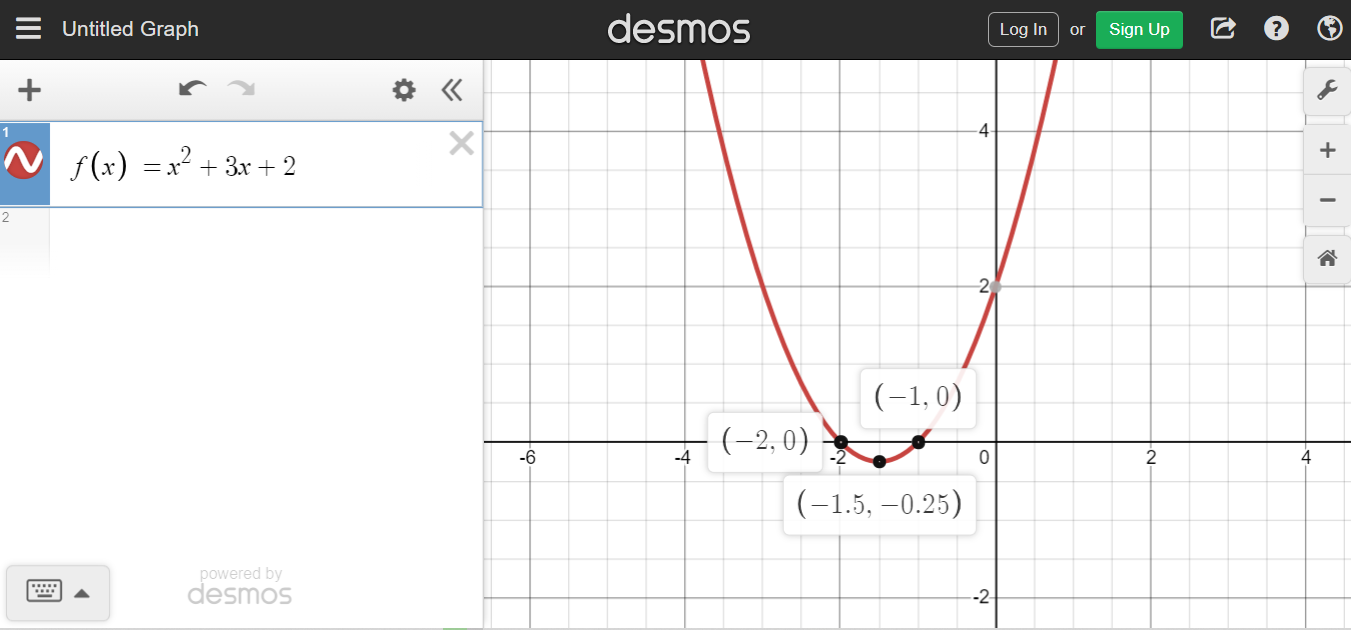
Screenshot Three: y = x^2 + 3x + 2, Vertex/Min of (-1.5, -0.25), Opens Up
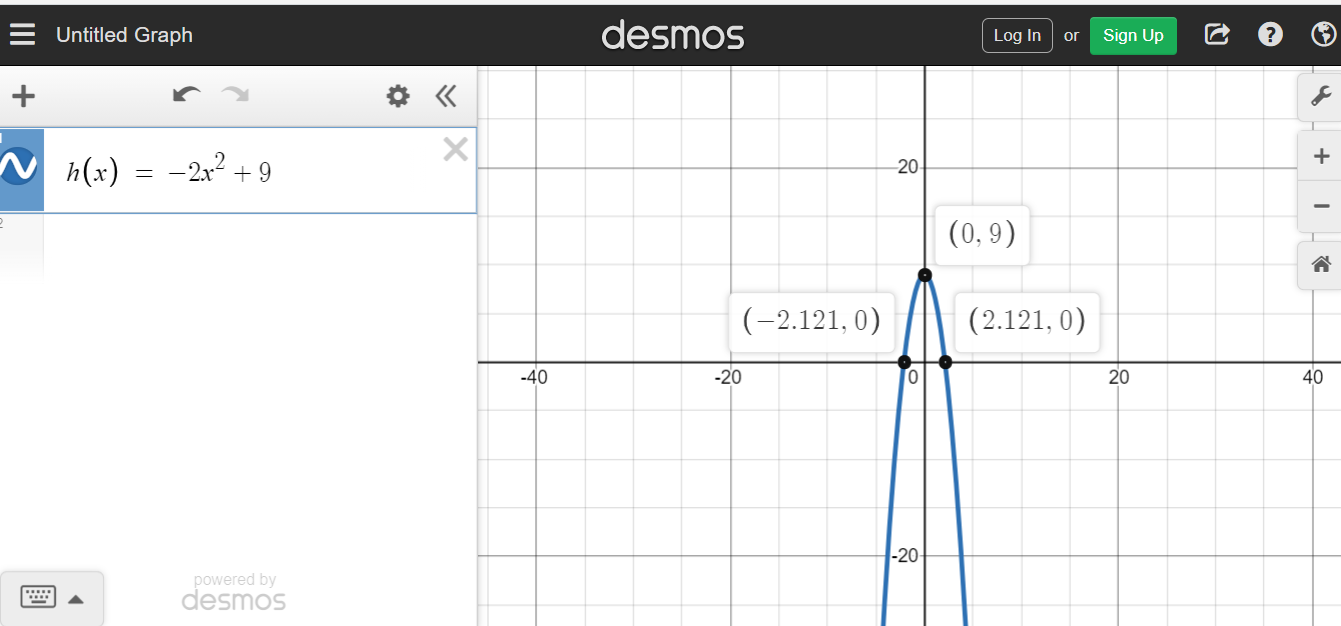
Screenshot Four: y = -2x^2 -2x - 10, Vertex/Max of (-0.5, 9.5), Opens Down
The Quick Formula
There are multiple ways to determine the vertex of a quadratic function. One way is through solving the quadratic equation through algebraic factoring methods. Once the two solutions or x-intercepts are found, add them both and divide by two to obtain the x-coordinate of the vertex. Use the x-coordinate to find the y-coordinate. A second way is a direct approach using the algebraic method of completing the square. The third way that I propose here is a fast and way less algebraic way of finding the vertex point of a parabola.
Quick Way Of Finding A Vertex
This quick way of finding the vertex is based from the quadratic formula. Given the quadratic function of the form  , the x-intercepts from the quadratic formula is given by:
, the x-intercepts from the quadratic formula is given by:
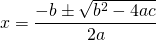
with
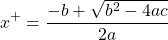
and
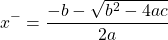
The x-plus and x-minus formulas are for obtaining the x-intercepts for a quadratic equation. If you want just want the vertex, you add the x-plus and x-minus values together and then divide by 2. This would take a while though. Consider this quick formula for the x-coordinate for the vertex (no derivation shown here).

This above value would be used to find y-coordinate of the vertex of the parabola. The vertex point would be of the form.
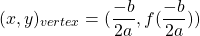
(given a quadratic function in f(x) notation)
Examples
It is important to show some examples to put theory into some sort of practice. The quick way of obtaining the vertex helps with quick sketches of parabolas. Why struggle with algebraic methods and then graph when you can use the quick method? Use this quick method when possible for plotting the vertex and save time. The quadratic formula may be used to find x-intercepts.
Example One
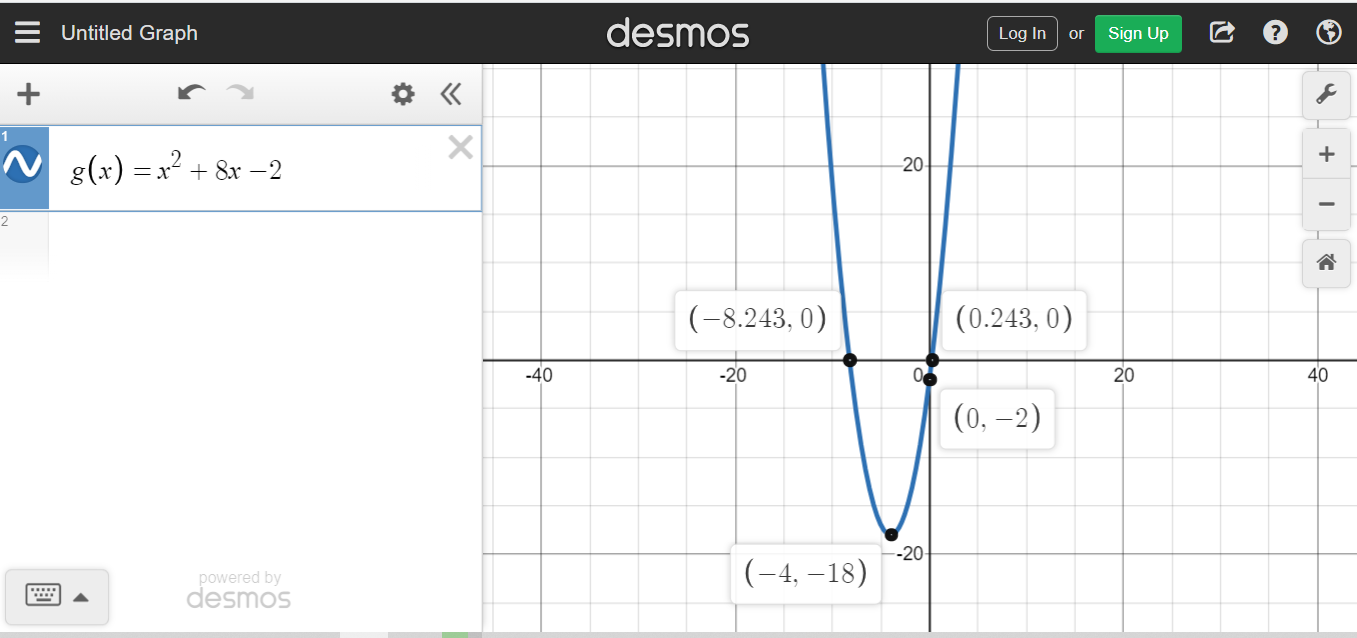
Determine the vertex point for the quadratic  .
.
The coefficients for this quadratic function are a = 1, b = 8 and c = -2. Apply the formula to obtain the vertex point.

This negative 4 is the x-coordinate for the vertex. Use this value to compute g(-4) which is the y-coordinate of the vertex (minimum).
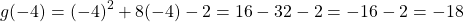
This vertex value is (-4, -18). I have included a screenshot as verification.
Example Two
What is the vertex for the quadratic 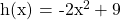
With this one the coefficients are a = -2, b = 0 and c = 9.

It follows that h(0) = 9. This vertex is a maximum at the point (0, 9).
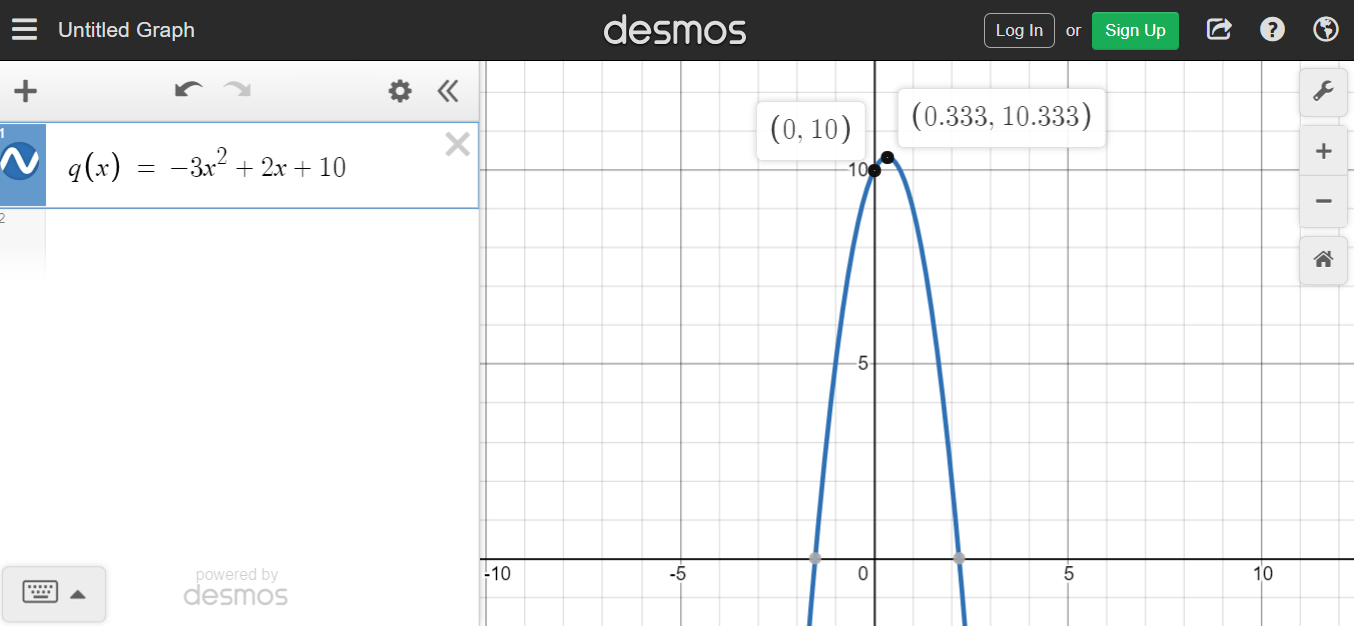
Example Three
Determine the vertex for  .
.
Use the quick formula again for obtaining the x-coordinate for the vertex.
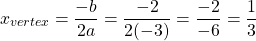
Using one-third for x gives:
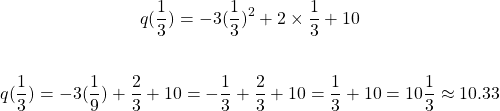
The vertex here is a maximum at (1/3, 10 1/3).
Notes On Application Problems
I have not included applications problems here. It would take some time for me to develop such problems. You can use this quick technique on quadratic equations that model business costs, business revenues and profits.
A parabola would be downward facing for a company modeling revenues or profits with a quadratic equation. Upward facing parabolas are related to minimum costs. Whether a business should use quadratic equations or not for business costs and revenues is a different topic.

Posted with STEMGeeks