¡Saludos y bienvenidos al presente blog! En esta ocasión me gustaría compartir a través de la plataforma Hive.blog un tópico de suma importancia para el cálculo de reacciones externas en sistemas isostáticos: las Ecuaciones de Condición. Con el objetivo de brindar una fuente de referencia para los tópicos que se abordan en la asignatura Estática Aplicada comparto esta publicación en la que bridaré un enfoque didáctico de este tema para su entendimiento satisfactorio.
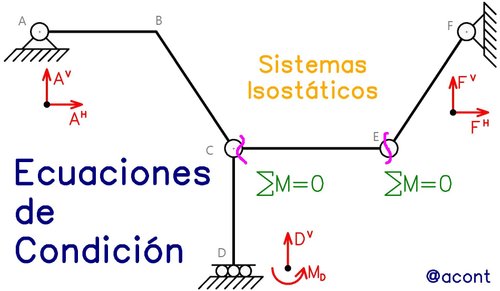
La anterior publicación abordó las Ecuaciones del Equilibrio Estático, las cuales podemos denominar como las ecuaciones generales o fundamentales:
•Las Ecuaciones de Equilibrio Estático y algunas aplicaciones en la Ingeniería Civil

Puede que surja la interrogante: si se tienen las tres ecuaciones de equilibrio estático ¿Para qué necesitamos las ecuaciones de condición? En el estudio de la Estática Aplicada, las tres ecuaciones de equilibrio estático para el cálculo de reacciones externas no suelen ser suficientes debido a la complejidad en el arreglo de los sistemas isostáticos en donde se tienen más de tres incógnitas externas, por lo que se requiere primero comprender y saber aplicar las ecuaciones de condición las cuales nos ayudan a hallar las reacciones externas aprovechando las condiciones de vinculación internas del sistema.
El análisis de sistemas isostáticos consiste en primera instancia en calcular las reacciones externas en los mismos ya este es el paso inicial y por ello constituye la práctica fundamental de la Estática, si no se efectúa con la suficiente presteza, el estudiante no tendrá un rendimiento óptimo en los temas subsiguientes del análisis de sistemas isostáticos e incluso en las asignaturas subsiguientes a Estática Aplicada en las que se da por sentado que se sabe efectuar el cálculo de reacciones externas.
Introducción
El análisis de sistemas isostáticos requiere primero comprender que son estos sistemas y que los caracterizan. Podemos definir un sistema isostático como un sistema material compuesto por “n” chapas (cuerpos rígidos) unidas entre sí por diferentes condiciones de vinculación y que además posee cero (0) grados de libertad, es decir, el grado mínimo de estabilidad (posee el número mínimo de restricciones que impiden su movimiento). En la publicación anterior se abordaron sistemas de solo una chapa (o n=1) y en esta ocasión, tenemos un número “n” igual o mayor a dos (n≥2). El ejemplo más básico de sistema isostático con dos chapas viene dado por el “arco triarticulado” que si bien puede no ser curvo tiene cierto parecido a un arco. Posee dos puntos articulados fijos a tierra y un punto de vinculación entre chapas, el cual viene dado por una rótula (Fig. N°1).
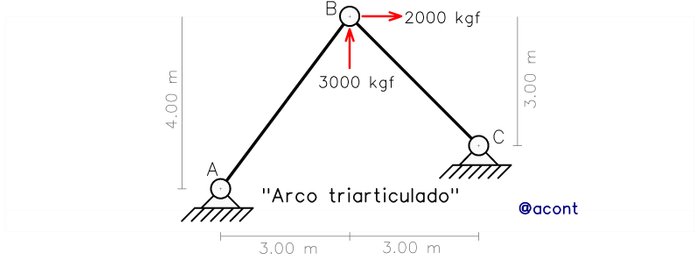
Debido a la restricción del movimiento en los apoyos a tierra, se generarán reacciones externas en los mismos en respuesta al sistema de cargas. En este caso se tendrán en total cuatro (4) reacciones externas o incógnitas (dos por cada articulación fija a tierra) y las tres ecuaciones generales de equilibrio estático no nos son suficientes, necesitaremos una ecuación adicional.
Ecuaciones de condición
Ante la presencia de solo una chapa, siempre tendremos tres incógnitas estáticas que podemos encontrar mediante las tres ecuaciones fundamentales del equilibrio estático, pero en el caso de un sistema de varias chapas vinculadas entre sí, aparecerán más de tres incógnitas externas, por lo que se necesitarán más ecuaciones para poder hallarlas todas. Dichas ecuaciones podemos obtenerlas a través de los vínculos internos y son las denominadas Ecuaciones de Condición (ecuaciones auxiliares o de construcción según algunas fuentes). Si bien las tres ecuaciones fundamentales del equilibrio también son condiciones, nos referiremos a estas simplemente como ecuaciones “generales” ya que las utilizaremos para garantizar el equilibrio general del sistema, mientras que internamente nos apoyaremos en las ecuaciones de condición.
En la Fig. N°2 observamos un sistema isostático parecido al que podría salir en su examen parcial, con un arreglo notablemente más complejo que el del “arco triarticulado” y se han evidenciado las reacciones externas a calcular.
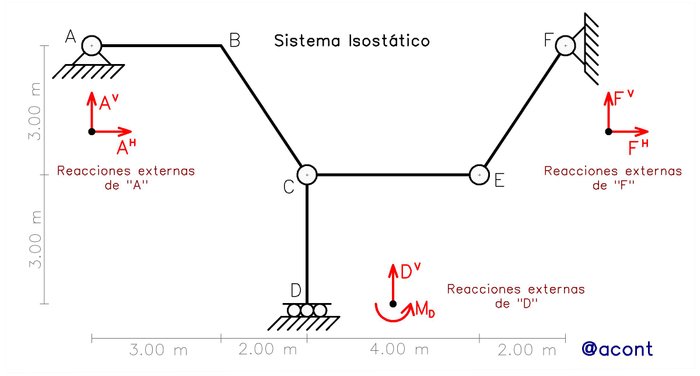
Este sistema nos servirá para distinguir entre los distintos casos en los que podemos utilizar las ecuaciones de condición sobre los vínculos internos. Ya que el sistema de cargas externas siempre estará presente y puede adoptar distintas configuraciones, obviaremos su representación y nos concentraremos en la aplicación de las ecuaciones de condición, de manera que en las ecuaciones planteadas la sumatoria de las cargas que actúan sobre el sistema aparecerá como “∑Cargas externas” asumiendo que sus valores son conocidos.
Nos concentraremos en los vínculos internos de 2° grado (rótulas y bielas paralelas) y en los de 1° grado (apoyo simple interno y el empotramiento libre interno) aunque estos últimos son poco frecuentes. Los vínculos internos de 3° grado (la junta rígida) no proporcionan ecuaciones de condición por lo que no nos servirán para el cálculo de reacciones externas.
Podemos empezar con el caso más común del uso de las ecuaciones de condición, el cual se da en las rótulas internas. Antes de darle un concepto o definición a las ecuaciones de condición, me gustaría primero mostrar de manera práctica como se originan y de qué forma las podemos utilizar, así se entenderá mejor lo que representan y la manera más efectiva de utilizarlas.
Imaginemos que el sistema de la Fig. N°2 se divide en dos, mediante un corte justo en la rótula “E”. Esto nos deja con dos subsistemas y nos concentraremos en el de la barra “EF”.
Producto del corte realizado quedan evidenciadas las reacciones o incógnitas internas, las cuales se transmiten de un subsistema a otro en igual magnitud y sentido opuesto para mantener el equilibrio interno. No nos interesa por ahora calcular estas reacciones internas, ya que estas incógnitas internas se calculan mediante un despiece de las barras del sistema y esto se realiza posterior al cálculo de las reacciones externas. Debemos tener claro cuáles son las restricciones internas que aporta cada vínculo. En el caso de la rótula, la rotación relativa de una barra respecto a la otra no está impedida, es decir, podemos suponer que podría existir allí rotación sin fricción si el sistema podría moverse. Recordemos que las restricciones son equivalentes a las incógnitas estáticas, por lo que en el corte realizado no existirá una incógnita de momento, sino las incógnitas dadas por la restricción relativa de desplazamientos que aporta la rótula. En la Fig. N°3 se evidencia el diagrama de cuerpo libre de la barra “EF” producto del corte realizado.
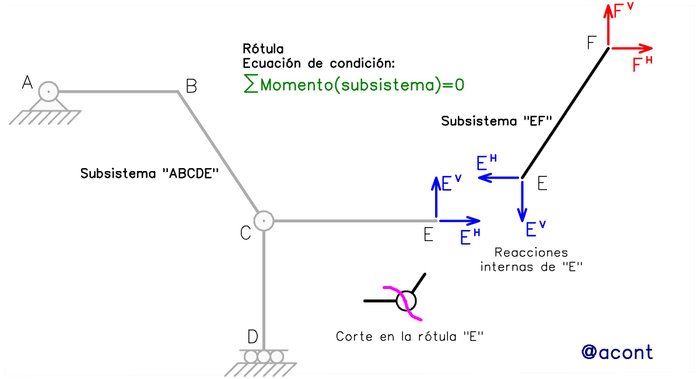
Se observa que planteando una sumatoria de momentos en el extremo “E” de la barra “EF”, podemos obtener una ecuación en la que solo aparecen incógnitas de interés (FH y FV), ya que las fuerzas incógnitas internas son concurrentes allí:
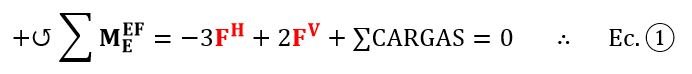
Podemos realizar exactamente lo mismo con la rótula en “C”, pero al ser una rótula que vincula tres barras, el corte se hace con el objetivo de “desvincular” la barra “CE” de la rótula, de manera que la rótula seguiría vinculando las otras dos barras y se evidencian las reacciones internas que se transmiten de un lado a otro (Fig. N°4).
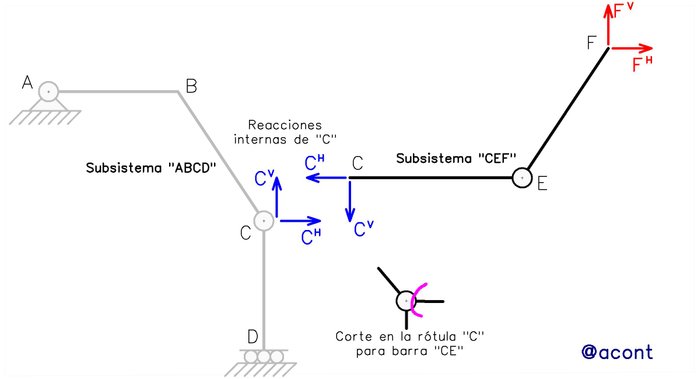
Igual que en el primer corte no aparecerá internamente una incógnita de momento y podemos aprovecharnos de esto para plantear sumatoria de momentos en el extremo de la barra “CE” tomando en cuenta todas las cargas e incógnitas externas del subsistema “CEF” (las incógnitas internas de “E” no aparecerán ya que el corte ahora se realizó en otro punto).
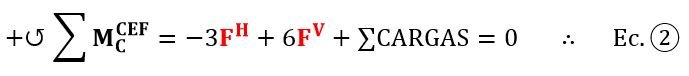
De esta manera obtenemos un sistema de dos ecuaciones con las mismas dos incógnitas el cual podemos resolver.
El arreglo del sistema nos obliga a plantear dos ecuaciones con dos incógnitas para hallar FH y FV. Pero es usual que algunas incógnitas se puedan calcular mediante una sola ecuación. Imaginemos que ahora se hace un corte en la rótula “C” pero esta vez “desvinculando” la barra “CD”. Obtendríamos un subsistema en el que mediante la sumatoria de momentos en el extremo “C” nos permitiría calcular MD:

Esto ocurre porque la reacción vertical del empotramiento móvil en “D” es una fuerza incógnita cuya dirección coincide con la rótula “C”, haciendo que su “brazo” de momento sea nulo en este punto y en la ecuación planteada solo aparecerá la incógnita de momento de “D”.
Si en un punto del sistema tenemos una chapa con solo un apoyo simple y existe una rótula cercana, el empleo de la sumatoria de momentos se hace más sencillo, ya que nos basta plantearla una vez para obtener la única incógnita proporcionada por el apoyo simple. En la Fig. N°5 se ha modificado el sistema para ilustrar esto.
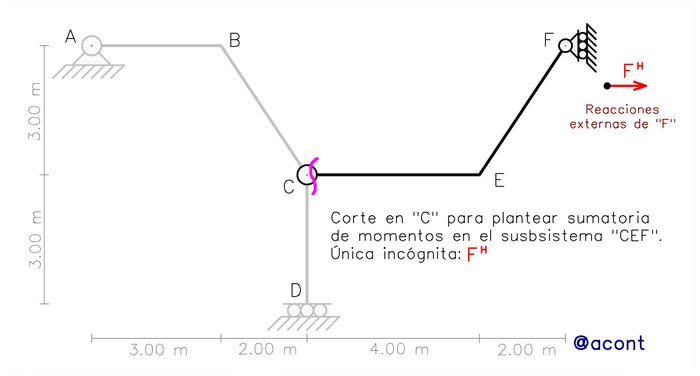
Ya vemos como se originan las ecuaciones de condición a partir de las rótulas internas y cómo podemos apoyarnos en ellas para calcular reacciones externas. Existen muchas definiciones para las ecuaciones de condición según la bibliografía referente a este tema, pero en lo personal pienso que la mayoría terminan siendo demasiado abstractas y poco útiles para el estudiante. Podemos definir las ecuaciones de condición como las ecuaciones que se pueden plantear en subsistemas generados a partir de cortes en los vínculos internos aprovechando la no existencia de algunas incógnitas en estos. La restricción que un vínculo interno no proporciona se traduce en una ecuación de condición. Por lo tanto, en el caso de sistemas planos donde se tienen tres (3) grados de libertad, si un vínculo interno es de 2° grado, tendrá una (1) ecuación de condición, y si el vínculo interno es de 1° grado, podemos obtener de él dos (2) ecuaciones de condición.
En el caso de las bielas paralelas, el principio es el mismo. Al ser un vínculo de 2° grado proporciona dos restricciones internas y permite un movimiento (desplazamiento relativo), por lo que, realizando un corte en las bielas paralelas se evidenciará la no existencia de una fuerza incógnita interna en la dirección perpendicular a las mismas (Fig. N°6).

En el subsistema formado por la barra “EF”, podemos observar en el extremo “E” la no existencia de una incógnita interna en la dirección perpendicular a la barra, esto nos permite plantear una sumatoria de fuerzas en dicha dirección de manera que en esta ecuación solo aparecerán las incógnitas de interés (las reacciones externas de “F”). Esto implica proyectar las reacciones horizontal y vertical de “F” en una dirección inclinada (además de las cargas externas que existan en dicha barra) por lo cual esto puede ser un proceso poco práctico. En consecuencia, una mejor forma de encontrar una ecuación que contenga a FH y FV suele ser plantear sumatoria de fuerzas horizontales y verticales para dicha barra, de manera que solo nos toque encontrar las componentes de solo una fuerza inclinada (la fuerza incógnita de las bielas paralelas) y posteriormente eliminar esta incógnita interna no deseada mediante una operación algebraica (se ha omitido la sumatoria de las cargas externas para una demostración más sencilla):

Obtenemos así una ecuación que contiene las dos incógnitas de “F”, y luego mediante la rótula en “C” obtenemos otra ecuación que contiene las mismas dos incógnitas (similar a como ya se hizo anteriormente). En esta ocasión se han utilizado las bielas paralelas en “E” y la rótula en “C” para calcular las dos incógnitas de “F”.
Cuando las bielas se encuentran inclinadas pueden llegar a ser un dolor de cabeza, pero si las hallamos de manera horizontal o vertical se simplifican en gran medida los procedimientos a realizar. En la Fig. N°7 se ha modificado el sistema haciendo que las bielas se encuentren en dirección horizontal.
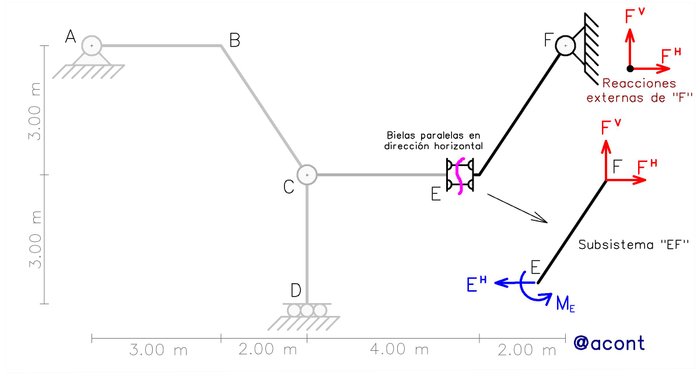
Haciendo un corte en las bielas, podemos notar que la fuerza incógnita interna se encuentra en dirección horizontal, por lo que mediante una simple sumatoria de fuerzas en dirección vertical en la barra “EF” podemos hallar la reacción vertical incógnita de “F”.

La sumatoria de fuerzas es la ecuación de condición que las bielas paralelas nos proporciona, puesto que al igual que la rótula nos permite ya sea hallar una ecuación que relacione dos incógnitas o calcular una si el subsistema producto del corte posee solo una incógnita en determinada dirección. La diferencia sustancial entre ambos vínculos internos de 2° grado es que las rótulas permiten incluir momentos incógnita en la ecuación de condición, mientras que, si tenemos las bielas paralelas, la sumatoria de fuerzas como ecuación de condición solo incluirá incógnitas como fuerzas puntuales. Esto representa una ventaja cuando se tienen bielas paralelas seguidas de una chapa apoyada a tierra mediante un “empotramiento móvil” ya que este vínculo posee dos incógnitas estáticas externas a calcular (un momento y una fuerza puntual) y la sumatoria de fuerzas como ecuación de condición nos permitirá no incluir este momento incógnita para lograr así calcular la fuerza incógnita. En la Fig. N°8 se observa esto:
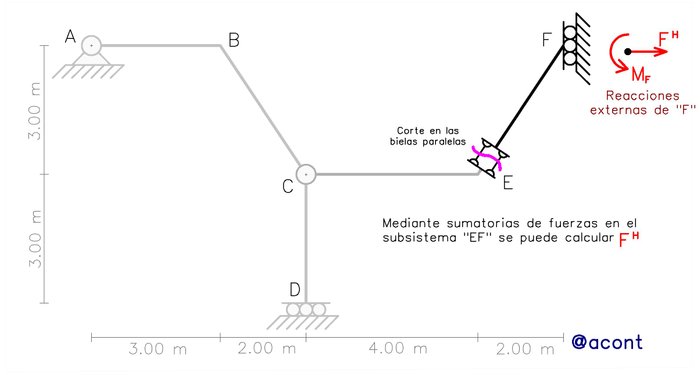
El corte en las bielas paralelas nos brindaría un subsistema en el que podemos realizar la sumatoria de fuerzas en vertical y horizontal, logrando calcular la reacción horizontal de “F”, para luego calcular el momento de “F” mediante una sumatoria de momentos en la rótula “C” (subsistema “CEF”).
Finalmente, los vínculos de 1° grado, aunque son poco usuales, la existencia de una sola incógnita interna nos permite obtener de estos dos (2) ecuaciones de condición, simplificando así la resolución de las reacciones externas. Básicamente tenemos dos tipos de vínculos de 1° grado.
El apoyo simple interno (“patín” interno o “rodillo interno“ dependiendo de su representación) es un vínculo que solo restringe un (1) desplazamiento relativo de una chapa respecto a otra, dejando libre la rotación y el desplazamiento en dirección perpendicular al desplazamiento restringido. También se le suele sustituir por la “biela simple” ya que cumple la misma función y se comporta como una barra de tamaño infinitesimal articulada en sus extremos con las chapas vinculadas. El siguiente sistema isostático posee un apoyo simple interno en “B” (Fig. N°9). Los subsistemas producto del corte en dicho vínculo se evidencian.
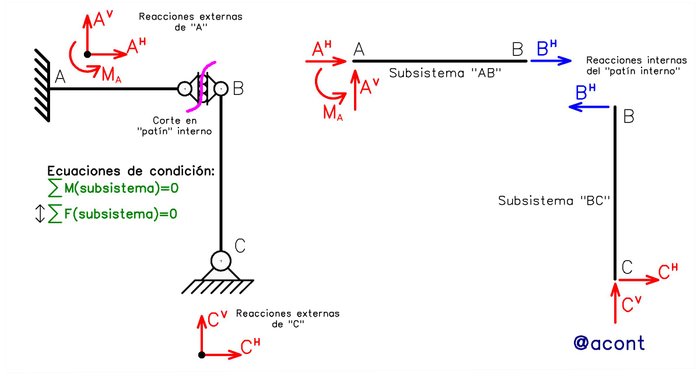
La sumatoria de fuerzas en dirección vertical para cualquiera de los dos subsistemas (al igual que con las bielas paralelas) nos permitirá hallar la reacción vertical de “A” y la reacción vertical de “D”. El momento planteado en el extremo “B” para el subsistema de la derecha nos permitirá (al igual que una rótula) obtener una ecuación que contenga las dos incógnitas de “D” pero como ya conocemos previamente la reacción vertical, podemos despejar la reacción horizontal de “D” mediante solo una operación. En cuanto a ecuaciones de condición, este vínculo interno es una especie de “combinación” entre la rótula y las bielas paralelas.
Solamente nos queda mencionar un vínculo: el empotramiento libre. Quizás este sea el menos frecuente de todos, pero a su vez es el que menos complejidad introduce en el cálculo de reacciones. Su efecto es el de restringir la rotación relativa entre dos chapas, dejando libre el desplazamiento en cualquier dirección. Esto se traduce en dos (2) ecuaciones de condición: sumatoria de fuerzas tanto en dirección horizontal como en dirección vertical. En la Fig. N°10 se ha sustituido el apoyo simple interno por un empotramiento libre interno en el sistema de la Fig. N°9. Se evidencian ambos subsistemas producto del corte en “B” y sus diagramas de cuerpo libre.
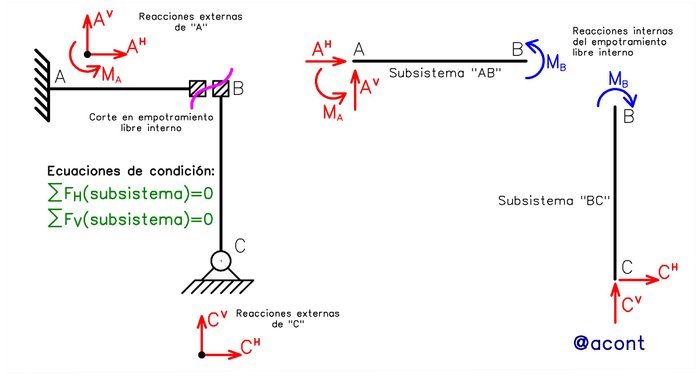
Solo existirá en “B” un momento interno transmitiéndose de una chapa a otra. Esto significa que en el extremo “B” de ambos subsistemas no existirán fuerzas incógnitas, y nos podemos aprovechar de esto para plantear sumatoria de fuerzas en cada subsistema sin que aparezcan incógnitas internas no deseadas. Para el sistema mostrado en la Fig. N°10, las ecuaciones de condición que nos otorga el empotramiento libre interno nos permite prácticamente calcular todas las reacciones externas, a excepción del momento en “A”, el cual podemos hallar mediante una sumatoria de momentos en cualquier punto del sistema.
Limitaciones algebraicas de las ecuaciones de condición
Para finalizar este abordaje teórico sobre las ecuaciones de condición, debemos tener en cuenta el factor algebraico de estas. Con esto me refiero a dos situaciones que se pueden presentar al utilizar las ecuaciones de condición de manera inefectiva.
La primera situación se refiere al planteamiento de sistemas de ecuaciones numerosas. Si un sistema posee por ejemplo cinco (5) incógnitas o reacciones externas, intentar calcularlas mediante un sistema de cinco ecuaciones con cinco incógnitas es una tarea muy poco práctica ya que las operaciones algebraicas se vuelven muy extensas y con fácil tendencia a errores, no es una tarea imposible, pero en lo personal no lo recomiendo. Las calculadoras científicas convencionales permiten resolver sistemas de hasta tres ecuaciones con tres incógnitas, y es la única herramienta de cálculo que el estudiante suele poseer.
La segunda situación se refiere simplemente al número de ecuaciones de condición independientes que se pueden plantear al mismo tiempo en un determinado vínculo interno. En general, casi todos los vínculos internos solo vinculan dos chapas, pero en el caso de las rótulas es común encontrar tres o hasta cuatro chapas vinculadas, por lo que el número máximo de ecuaciones de condición “independientes” que se pueden obtener en una rótula es equivalente al número de barras que concurren a ella menos uno (1). Es decir:
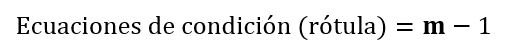
Donde “m” es el número de barras. Por lo que, si una rótula vincula dos barras, solo podremos plantear una ecuación de condición independiente en ese punto, y no dos como podría pensarse. Esto conduce a que en ocasiones la utilización de sistemas de numerosas ecuaciones podría resultar en errores de redundancia, en los que no se podrá hallar la solución a dichos sistemas por que se pueden llegar a tener ecuaciones no independientes (sistema de ecuaciones incompatible). Esto de las “ecuaciones independientes” que aporta una rótula quizás se pueda entender mejor a través del sistema isostático de la Fig. N°1.
Al ser cuatro las incógnitas, plantearemos cuatro ecuaciones. Tomaremos tres opciones diferentes para el sistema de ecuaciones para ver cuál de ellos posee ecuaciones dependientes (Fig. N°11).
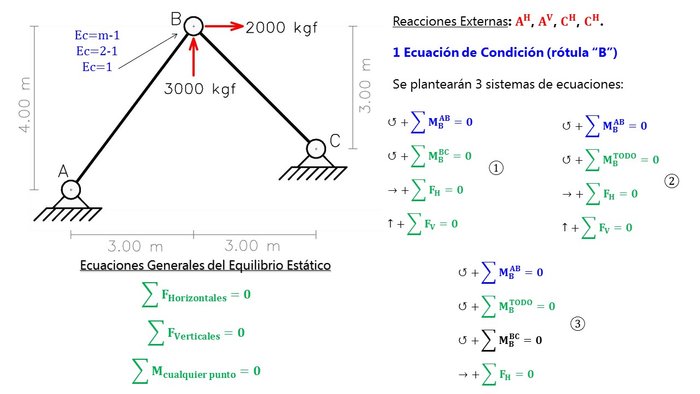
Mediante una herramienta de cálculo (Derive) se ha hallado el determinante de la matriz equivalente para cada sistema de ecuaciones. Del álgebra lineal sabemos que si el determinante resulta ser nulo el sistema es incompatible (Fig. N°12).
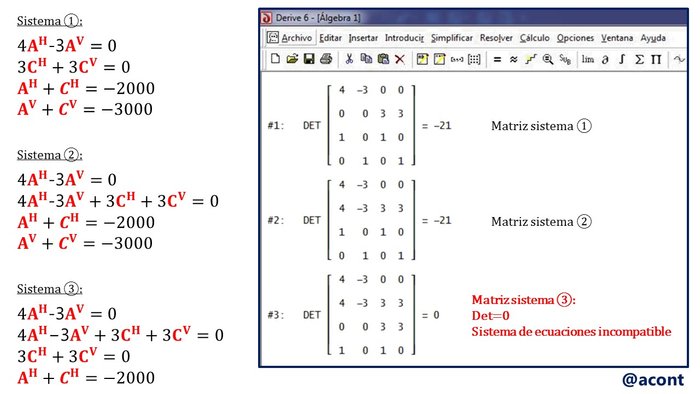
El tercer sistema de ecuaciones resulta ser el que está mal planteado. Pero en las otras dos hemos utilizado la rótula dos veces ¿Por qué no resultaron ser incompatibles? Tenemos tres opciones para la rótula: una sumatoria de momentos para cada subsistema y una sumatoria de momentos general (para todo el sistema). Al “utilizar” la rótula dos veces estamos agotando la vía de la única ecuación de condición que nos ofrece, pero de las tres ecuaciones fundamentales de equilibrio estático tenemos también una que nos permite plantear sumatoria de momentos en cualquier punto, y esa es la otra opción que tenemos, una tercera ecuación sería dependiente de las dos primeras.
Así que en este ejemplo la rótula no aporta dos ecuaciones de condición, sino que también tenemos una de las tres ecuaciones generales de equilibrio. Este es un detalle teórico a tener en cuenta. Se han planteado cuatro ecuaciones para demostrar cómo nos afecta el mal uso de las ecuaciones de condición. Sin embargo, este sistema se puede resolver de manera muy simple, similar a la situación en las Fig. N°3 y N°4, donde se plantean dos ecuaciones con dos incógnitas, solo que en este caso plantearemos una sumatoria de momentos en la rótula “B” (ecuación de condición) y otra en “A” o en “B” para anular dos incógnitas y quedarnos con las otras dos.
En consecuencia, para evitar estos inconvenientes algebraicos personalmente recomiendo procurar calcular cada reacción por separado mediante una ecuación única de esta manera evitamos operaciones algebraicas muy extensas y no debemos preocuparnos por el trasfondo teórico del “número de veces que nos sirve un vínculo interno”, ya que en ningún momento vamos a juntar varias ecuaciones en un sistema. El objetivo es hallar las incógnitas, de la manera más simple y práctica. Solo en el caso de que no haya otra opción (como por ejemplo los sistemas de las Figuras N°2, N°4 y N°6) se plantearán sistemas de ecuaciones de máximo dos (2) o incluso hasta tres (3) incógnitas. Si un sistema isostático amerita el planteamiento obligatorio de sistemas de ecuaciones con más de tres incógnitas, este podría ser demasiado complicado para fines académicos.
Conclusiones
Referencias Bibliográficas
[1]Norris, C. H. y Wilbur, J. B. (1973). Análisis Elemental de Estructuras. Segunda Edición. Libros McGraw-Hill de México. (p. 69, 72-73, 79-80).Fuente
[2]Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 69-71).Fuente
Material recomendado
•Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad
•Cálculo de reacciones externas mediante el Principio del Trabajo Virtual para Cuerpos Rígidos
Imágenes de autoría propia realizadas mediante LibreCAD y ecuaciones elaboradas mediante Microsoft Word. Figuras N°11 y N°12 realizadas con Microsoft PowerPoint.
Visite la etiqueta #STEM-espanol para encontrar contenido de calidad en habla hispana referente a Ciencias, Tecnología, Ingeniería, Matemáticas y otros tópicos relacionados. @STEM-espanol es una comunidad dedicada a la difusión de contenido en español referente a STEM (ciencia, tecnología, ingeniería y matemáticas por sus siglas en inglés) conformada por autores de todo el mundo.
Para mayor información y si deseas publicar contenido STEM acá está el enlace de invitación al canal de Discord de #STEM-espanol: https://discord.gg/UJwQXWP donde puedes presentarte y aclarar dudas.

STEMsocial es un proyecto en la plataforma Hive al cual #STEM-espanol está adscrito, cuyo objetivo es crear un nuevo paradigma de comunicación STEM en Hive.
Ing. Angel Contreras
Congratulations @acont! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Vote for us as a witness to get one more badge and upvotes from us with more power!
Thanks.
You're welcome @acont! Great job! Hive on and stay safe❤️
cheers, liz
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
Please consider using the STEMsocial app app and including @steemstem as a beneficiary to get a stronger support.
Agradecido por su apoyo.
Estos diagramas están verdaderamente geniales. Que programa utilizas para los cálculos? @acont
Saludos cordiales @carloserp-2000 he utilizado en este caso el programa "Derive" el cual es una herramienta de cálculo capaz de hacer operaciones con matrices para demostrar la incompatibilididad del sistema de ecuaciones N°3. En realidad estos ejercicios son resueltos por los estudiantes mediante lapiz, papel y calculadora, por ello se hace necesario el entendimiento y uso eficiente de las ecuaciones de condición.
Acá la interfaz del programa:
Permite una variedad de operaciones, es sencillo y ligero, quizás sea un poco engorroso a la hora de introducir manualmente algunas operaciones. Gracias por su comentario, siempre busco que las figuras sean atractivas desde el punto de vista visual y entendibles.