¡Saludos estimados lectores de la plataforma HIVE! En la anterior publicación se abordó el despiece de los sistemas isostáticos:
•Metodología para realizar el despiece de Sistemas Isostáticos
En la cual se determinó a través de una metodología el cálculo de las reacciones internas que se transmiten de una barra a otra, tomando en cuenta ciertos casos particulares como lo son las cargas concentradas en las juntas y juntas en las que concurren más de dos barras. Los elementos lineales del sistema isostático (barras) son analizados uno a uno evidenciando las cargas tanto externas como internas que actúan sobre cada uno de ellos. Al final de dicho artículo planteé la siguiente interrogante: ¿Cómo se obtienen las reacciones en los extremos de las barras inclinadas según el sistema local (direcciones longitudinal y perpendicular a la barra)?. Esto lo abordaremos en la presente publicación.
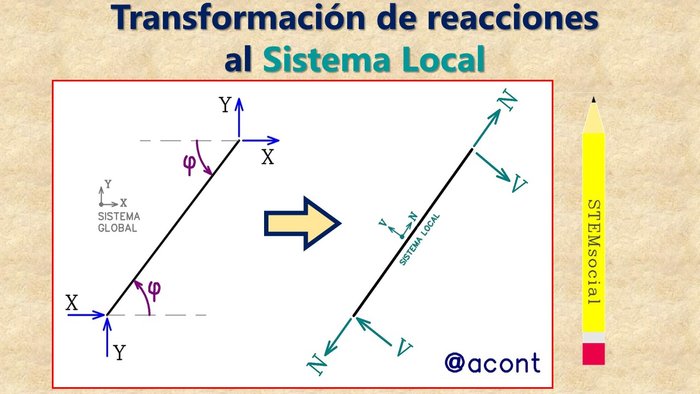
Puesto que estaremos de nuevo hablando del tema de las solicitaciones, recomiendo la lectura del artículo siguiente:
En dicho artículo se realiza un abordaje sobre las solicitaciones locales en el plano (fuerza axial, fuerza cortante y momento flector). Las solicitaciones juegan un papel muy importante en el diseño estructural de obras civiles, puesto que principalmente son ellas las que dictan las dimensiones que tendrán los diversos elementos estructurales para soportar las cargas. En la asignatura Estática Aplicada se introduce este concepto a los estudiantes y se da el primer paso hacia lo que es la Ingeniería Estructural.
Se ha recopilado todo el material sobre Estática Aplicada en la siguiente publicación:
Material de Estática Aplicada
Introducción
Recordemos que las solicitaciones son reacciones internas que actúan en cualquier punto del sistema y se generan ante la aplicación de cargas externas. Si un sistema estructural está siendo solicitado por cargas externas, es porque dichas cargas generan fuerzas axiales, cortantes y momentos flectores en sus elementos. También existen otros tipos de solicitaciones, pero estas tres son las más usuales al tratarse de sistemas planos con cargas en el plano.
Cuando realizamos el despiece de sistemas isostáticos, estamos hallando sus reacciones internas según un sistema de referencia global o general, es decir, en las direcciones horizontal o “X” y vertical o “Y”. Estas reacciones internas también pueden denominarse como solicitaciones generales. Las solicitaciones locales están orientadas según un sistema referencia particular para cada elemento lineal, es decir, tenemos un eje axial o longitudinal y otro eje perpendicular a la barra. En la Fig. N°1 podemos ver la diferencia entre ambos tipos de solicitaciones.
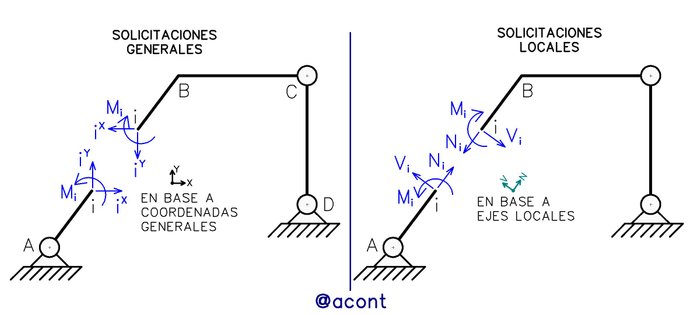
El momento flector no varía para ambos sistemas de referencia ya que este actúa alrededor de un eje perpendicular al plano, por lo que son las fuerzas internas las que se ven afectadas en magnitud y dirección al cambiar del sistema global al sistema local y viceversa.
Relaciones geométricas de solicitaciones
Al realizar el despiece, las barras que están inclinadas quedan expuestas a solicitaciones generales en sus extremos, en cambio las barras horizontales y verticales poseen solicitaciones en sus extremos tanto generales como locales (Fig. N°2).
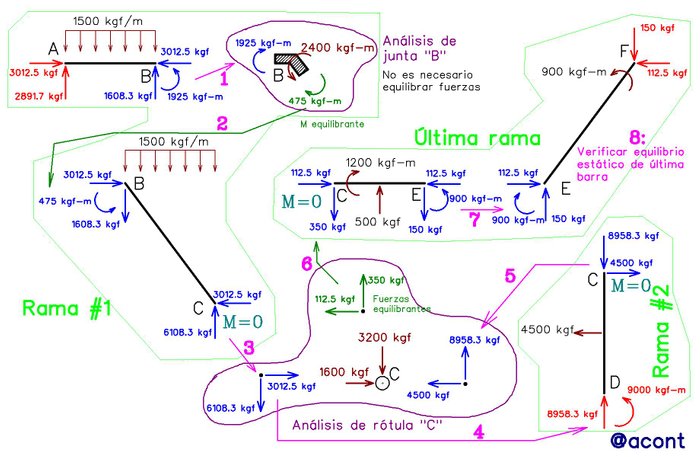
Ahora ¿Cómo se hace para transformar estas reacciones en los extremos de las barras inclinadas al sistema local?
Para realizar esto utilizaremos Relaciones Geométricas, es decir, ecuaciones que relacionan geométricamente las solicitaciones generales con las locales y la inclinación de la barra. También tenemos un método alternativo el cual se basa en proyectar las reacciones existentes sobre un par de ejes propuestos.
Pero ¿Cuál es el objetivo de hacer esto con las barras inclinadas? ¿Qué se busca con esto?
Al encontrar las solicitaciones locales que actúan en el extremo de cada barra, estamos encontrando las fuerzas axiales y fuerzas cortantes que actúan allí. Si nos vamos al ámbito ingenieril, en el caso de elementos estructurales, estas son las fuerzas que generalmente se utilizan para realizar el diseño de los mismos, determinando de esta manera sus dimensiones y otros criterios de diseño. En líneas generales, se suelen buscar las solicitaciones locales de fuerza axial y fuerza cortante en los extremos para efectos de diseño.
Y la razón principal para efectuar esto en las barras inclinadas, es que ello nos permite realizar los Diagramas de Solicitaciones de las mismas, es decir, un estudio detallado de las solicitaciones locales que actúan a lo largo del elemento lineal. La solicitación de mayor importancia en los elementos estructurales en general, es quizás el momento flector. En sistemas isostáticos, no es posible realizar el diagrama de momentos flectores de una barra inclinada sin antes conocer la fuerza cortante en uno de sus extremos. De igual manera, también podemos realizar diagramas del comportamiento de las fuerzas axial y cortante a lo largo de una barra sometida a cargas externas.
Ahora, volviendo con las relaciones geométricas de solicitaciones, tenemos que se dan mediante las siguientes ecuaciones, las cuales provienen de la matemática, utilizadas en la transformación de coordenadas para ejes cartesianos que sufren alguna rotación (Fig. N°3):
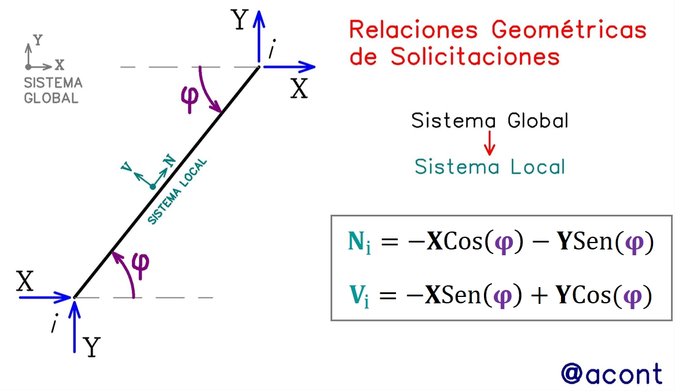
Estas ecuaciones no parecen muy complicadas, pero hay ciertas cosas a tener en cuenta antes de utilizarla para no obtener resultados erróneos.
“Ni” y “Vi” son las fuerzas axial y cortante respectivamente. Cabe destacar que “i” representa cada extremo, es decir, cada extremo de la barra inclinada puede tener valores diferentes de fuerza axial y cortante respecto al otro extremo.
Las fuerzas (reacciones) horizontal y vertical que existen originalmente (“X” y “Y”) se asumen positivas si se dirigen hacia la derecha y hacia arriba respectivamente. En caso de tener valores negativos de “X” o “Y” el signo negativo (-) de estas fuerzas se le adiciona al que existe originalmente en ambas ecuaciones.
Se debe tener cuidado con el ángulo “φ“. Este ángulo lo vamos a medir siempre desde la horizontal, siendo siempre un ángulo entre 0° y 90°, sin importar en que extremo de la barra estemos. En la Fig. N°4 podemos observar las cuatro diferentes situaciones para el ángulo “φ“ dependiendo del cuadrante donde nos encontremos dada la inclinación de la barra y el extremo “i” de interés.
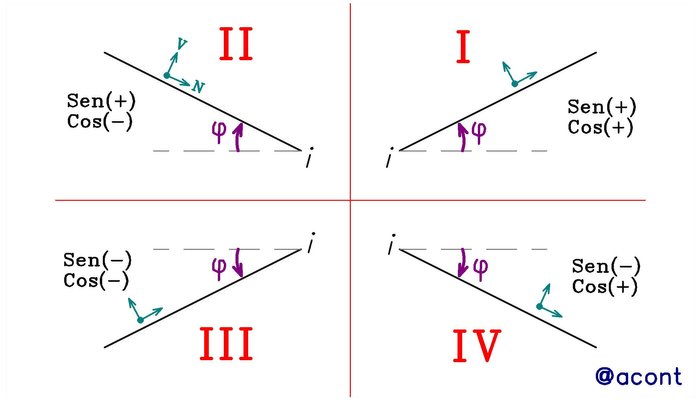
Pero en ningún momento calcularemos la magnitud del ángulo “φ“, ya que siempre utilizaremos el equivalente de las identidades Sen y Cos(, cateto opuesto y cateto adyacente sobre hipotenusa (CO/HIP y CA/HIP), ya que la magnitud de estos catetos siempre es conocida y la hipotenusa la obtenemos mediante el Teorema de Pitágoras. Es de suma importancia tomar en cuenta el signo que adquieren estas dos identidades trigonométricas en cada cuadrante, pero no hay que preocuparse, si no nos sabemos de memoria estos signos lo podemos chequear mediante una calculadora, viendo el signo del resultado de Sen(φ) y Cos(φ) para un ángulo cualquiera “φ” de cada cuadrante.
Por ejemplo, del tercer cuadrante podríamos tomar el ángulo 190°, y comprobar que la calculadora arroja un resultado negativo tanto para Sen(190°) como para Cos(190°).
Estos detalles con los signos suelen ser fuente de errores para los estudiantes.
Si se siguen estas recomendaciones respecto a los signos entonces estas ecuaciones nos darán siempre resultados correctos. En lo personal, estas ecuaciones me parecen el mejor método para lograr el objetivo de esta publicación. Sin embargo, también tenemos otro método alternativo utilizado por algunos profesores el cual explicaré más adelante.
Ejemplos prácticos de las relaciones geométricas.
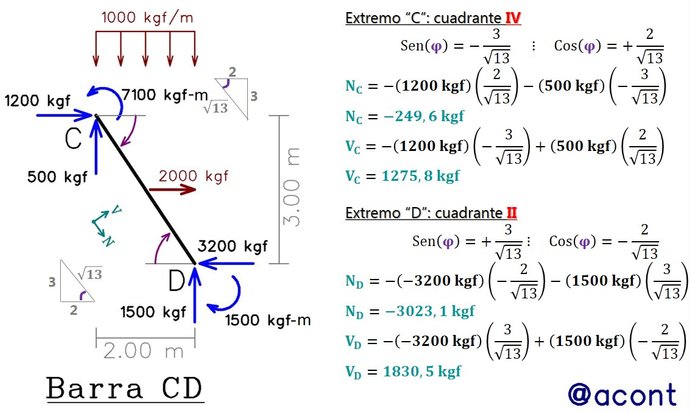
Tenemos las siguientes barras inclinadas (“AB” y “CD”), con las reacciones evidenciadas en sus extremos según el sistema global (solicitaciones generales) y se busca determinar las solicitaciones locales en sus extremos (Fig. N°5 y Fig. N°6):
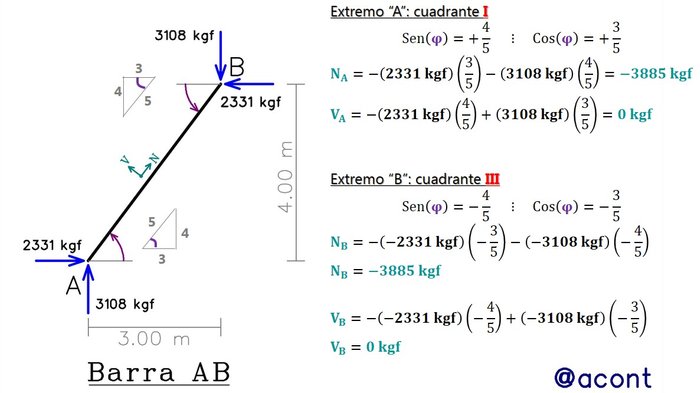
Como podemos observar en la Fig. N°5, en ambos extremos de la barra “AB” se obtuvo el mismo resultado para las fuerzas axiales y cortantes, por lo tanto, podemos asumir que, si no existen cargas externas puntuales o distribuidas en la barra inclinada, se puede hacer el cálculo para solo un extremo obviando que en el otro se obtendrán los mismos valores.
Otro resultado a destacar es que la fuerza cortante en ambos extremos es nula, la barra solo está sometida a fuerza axial. Esto suele ocurrir en casos donde en alguno de los dos extremos se encuentran bielas paralelas en dirección de la barra, recordando que la fuerza interna en dirección perpendicular a las bielas es nula. También puede darse el caso en el que la fuerza axial en un extremo es nula porque las bielas paralelas se encuentran allí orientadas en dirección perpendicular a la barra.
En el ámbito ingenieril, existen elementos estructurales unidimensionales inclinados sometidos únicamente a fuerza axial, el caso más común se presenta en las cerchas, también conocidas como armaduras o celosías. Estos son sistemas estructurales cuyos elementos están siendo solicitados únicamente por fuerzas axiales y pueden verse en puentes, techos, cubiertas, pasarelas, grúas-torre, etc.
En la Fig. N°6 tenemos una barra con cargas externas aplicadas, por lo que, para mantener el equilibrio estático el valor de las reacciones en ambos extremos no es el mismo, haciendo que los valores de fuerza axial y cortante varíen de un extremo a otro.
Una vez obtenidos los resultados de “N” y “V” en los extremos de cada barra, podemos observar que algunos valores son positivos y otros negativos, entonces ¿Qué dirección tomarán estas fuerzas en el extremo de la barra? Recordemos que las solicitaciones locales siguen la siguiente convención de signos (Fig. N°7):
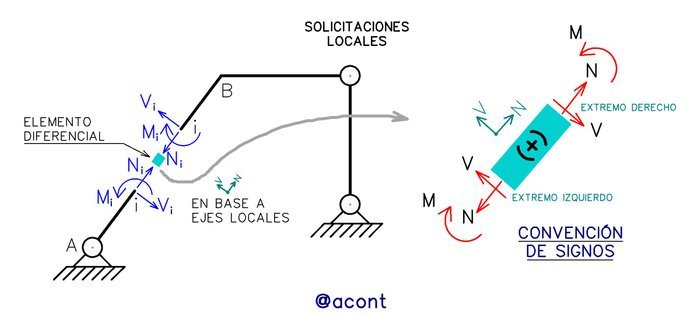
Primero, debemos asumir para cada barra unos ejes locales que nos indicarán cual es el extremo izquierdo y cual el extremo derecho de la misma. La fuerza axial “N” resulta positiva en tracción (hacia “afuera” de la barra). Mientras que, por ejemplo, una fuerza cortante “V” negativa en el extremo derecho de la barra nos indica que esta fuerza cortante se dirige hacia “arriba”.
Tomando en cuenta esto, ya podemos representar las solicitaciones locales en cada barra (Fig. N°8).
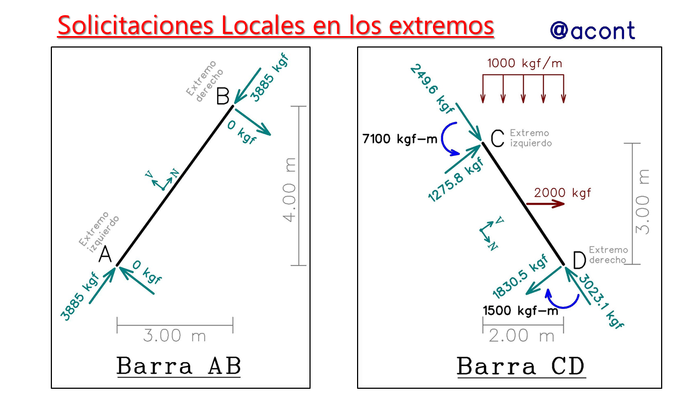
Estas son las fuerzas axiales y cortantes que actúan en los extremos de cada barra. Ambas resultaron estar sometidas a fuerzas axiales de compresión, mientras que la fuerza cortante es nula en la primera y positiva para la segunda, con un valor mayor en el extremo “D”.
Si quisiéramos conocer el valor de estas solicitaciones a lo largo de toda la barra se deberán elaborar sus diagramas, evidenciando cómo varían las mismas según gráficas que describen su comportamiento. De esta manera, podríamos detallar, por ejemplo, cómo varió la fuerza cortante en la barra “CD” de un valor menor a uno mayor, si este comportamiento es lineal o parabólico, y observar el efecto que tienen las cargas externas sobre las solicitaciones locales internas. En próximas publicaciones estaré abordando los Diagramas de Solicitaciones.
Método alternativo
Existe otro método, un poco menos sofisticado, el cual consiste en proyectar las fuerzas existentes en los extremos sobre dos ejes similares a los ejes locales, y hallar la resultante sobre cada uno. Esto implica asumir un sentido positivo para estos ejes que no necesariamente sigue la convención de solicitaciones locales descrita anteriormente.
Vamos a aplicar este método en el extremo “D” de la barra “CD” (Fig. N°9).
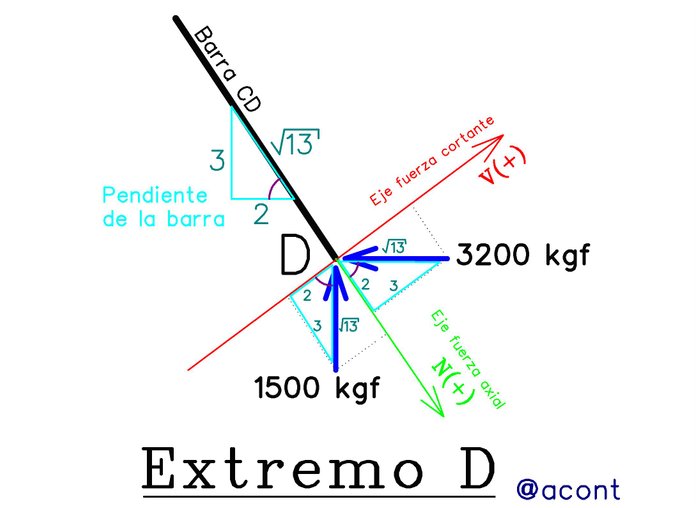
Se han generado dos ejes “N” y “V” longitudinal y perpendicular a la barra respectivamente, cuyo sentido positivo se asumió arbitrariamente. Para proyectar las fuerzas sobre dichos ejes, personalmente recomiendo no aplicar las directamente identidades trigonométricas sino utilizar la pendiente de la barra para obtener un triángulo cuyos catetos son las distancias conocidas (2.00 y 3.00 metros) y su hipotenusa se puede calcular mediante el Teorema de Pitágoras.
Dicho triángulo (en azul claro) se puede representar de manera equivalente sobre la proyección de las reacciones existentes (en azul), fijando uno de sus ángulos (en morado) para así ubicar correctamente los catetos (cateto adyacente=2 y cateto opuesto=3) en la proyección de las reacciones sobre los ejes “N” y “V”.
De esta manera, cuando realicemos la sumatoria de fuerzas en dirección de determinado eje, vamos a multiplicar la reacción existente por el cateto paralelo a dicha dirección entre la hipotenusa.
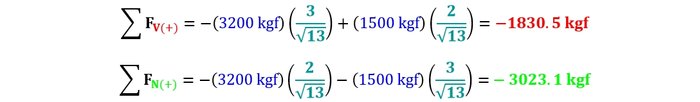
Tal como se observa, hemos obtenido los mismos resultados en magnitud y sentido (fuerza axial en compresión y fuerza cortante hacia abajo). Quizás sea un poco complicado asimilar esta manera de proyectar las fuerzas a la primera vez, pero es mucho más efectiva que calcular un ángulo y luego multiplicar las fuerzas por el Seno o el Coseno de dicho ángulo, sobre todo si se debe hacer esto repetidas veces.
Si nos fijamos en la estructura de las expresiones planteadas, vemos que poseen mucha similitud con las ecuaciones dadas por las relaciones geométricas anteriores, por lo que esta es una manera equivalente de aplicarlas, solo que en este caso nosotros asumimos un sentido positivo en vez de obtener un resultado que automáticamente sigue una convención de signos.
Para finalizar, invito al lector a revisar la barra “CD” en la Figura N°8, allí se observa que en sus extremos las reacciones se han transformado al sistema local, pero seguramente surge la siguiente pregunta: ¿Debe hacerse lo mismo con las cargas externas las cuales actúan de manera inclinada respecto a esta barra?
Si se buscan realizar los diagramas de solicitaciones de dicha barra, debemos conocer de antemano no solo las reacciones en sus extremos según el sistema local, sino que las cargas externas también deberán proyectarse al sistema local para así conocer sus componentes en dirección longitudinal y perpendicular a dicha barra. Esto implica proyectar la carga puntual de 2000 kgf y la carga distribuida de 1000 kgf/m en sus componentes locales para dicha barra inclinada.
Tal como el lector seguramente ha constatado, el análisis de las barras inclinadas en sistemas isostáticos puede llegar a ser algo complicado, sobre todo si tenemos cargas externas aplicadas sobre ellas. Es por ello que la próxima publicación será dedicada a la proyección de cargas externas al sistema local, para así preparar el terreno para la elaboración de los diagramas de solicitaciones.
Conclusiones
•Los sistemas isostáticos están sometidos a solicitaciones cuando se le aplican cargas externas y para estudiar con más detalle el comportamiento de las mismas sobre los elementos del sistema (barras) es necesario conocer primero las solicitaciones locales que actúan en el extremo de cada barra.
•Las relaciones geométricas de solicitaciones permiten llevar las reacciones obtenidas del despiece del sistema global al sistema local en las barras inclinadas a través de ecuaciones que relacionan ambos sistemas entre sí. Poner en práctica el cálculo de solicitaciones en Estática Aplicada es la iniciación del estudiante en la rama del cálculo estructural.
•La elaboración de los diagramas de solicitaciones permite visualizar con detalle la variación de las mismas a lo largo de un elemento lineal, pero es necesario primero poner en práctica los procedimientos para llevar las reacciones y cargas externas al sistema local en el caso de las barras inclinadas.
Referencias Bibliográficas
[1]Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 69-74).Fuente
Material recomendado
•Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad
•Las Ecuaciones de Equilibrio Estático y algunas aplicaciones en la Ingeniería Civil
•Abordaje sobre las Ecuaciones de Condición en Sistemas Isostáticos
•Metodología para el cálculo de reacciones externas en Sistemas Isostáticos
Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft Word. Imagen de portada y Figuras N°3, 5, 6 y 8 elaboradas mediante Microsoft PowerPoint.
Publicado mediante STEM.OpenHIVE
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con más de tres años de trayectoria conformada por autores de todo el mundo en la que se comparte y aprecia el contenido STEM de calidad entre sus usuarios.
Para mayor información y si deseas publicar contenido STEM acá está el enlace de invitación al canal de Discord de #STEM-espanol: https://discord.gg/UJwQXWP donde puedes presentarte y aclarar dudas.

Créditos de la imagen: @glass.wolf

¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Hive Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Te invitamos a suscribirte a nuestra COMUNIDAD, apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Te informamos que el PROYECTO ENTROPÍA ha puesto en marcha un nuevo servicio, la Creación de cuentas nuevas de Hive, para más información puedes visitar este enlace.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Muchas gracias @entropia!
Excelente artículo compañero @acont. Muy didáctica la explicación para el proceso de descomposición de las fuerzas. Gracias por compartir conocimientos con la comunidad. Sin lugar a dudas tu blog está bastante enriquecido para fortalecer las competencias en este interesante campo de estudio como lo es la "Estática". Muchos éxitos y bendiciones. Saludos desde Perú!
Saludos compañero @eliaschess333, gracias por tu visita, éxito y saludos desde Vzla!
Congratulations @acont! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board And compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Thanks for using the STEMsocial app and including @stemsocial as a beneficiary, which give you stronger support.
Saludos @acont, felicitaciones tus entradas ya se convierten en un referente académico para #stem-espanol.
✍ A modo de recordatorio, este jueves 04 de junio, a partir de las 16:00 hrs (04:00 pm) hora de Venezuela, se retomarán los Conversatorio Virtuales, actividad que estará desarrollando el Dr. Tomás Pérez actual Coordinador del área #Educación-stem, y conocido en la plataforma HIVE como @tomastonyperez, la actividad se llevará a cabo en Discord en el servidor de @stem-espanol en el canal #Conversatorio, habrán 3 sorteos de 5 Hive para los usuarios que asistan a esta interesante actividad académica.
Gracias Prof. por su visita a mi blog! Excelente, esperando el conversatorio de mañana, gracias por el recordatorio, saludos.
Error en Fig. N°8 corregido.