¡Hola mis amigos de Hive blog!
Reciban un cordial saludo.
Los conceptos de energía inherentes a sistemas mecánicos son de gran utilidad ya que permiten obtener una descripción completa del sistema sin que sea necesario trabajar de forma directa con las fuerzas que gobiernan el fenómeno.
En el caso de los fenómenos electrostático, la energía es también un parámetro determinante en el análisis de dichos fenómenos. El carácter escalar de la energía electrostática y su relación con las fuerzas y campos presentes, permite una descripción más simple en términos matemáticos del fenómeno que se estudia y puede además ser usada para la determinación de los campos eléctricos que originan las diferencias de energía potencial generadas por distintas distribuciones de carga.
En el sistema que se muestra a continuación se observa una distribución de carga generadora de un campo electrostático, en cuyo entorno una carga de prueba 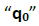 experimenta una diferencia de energía potencial
experimenta una diferencia de energía potencial 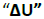 cuando esta es desplazada entre los puntos identificados como A y B.
cuando esta es desplazada entre los puntos identificados como A y B.
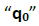 experimenta una diferencia de energía potencial
experimenta una diferencia de energía potencial 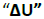 cuando esta es desplazada entre los puntos identificados como A y B.
cuando esta es desplazada entre los puntos identificados como A y B. 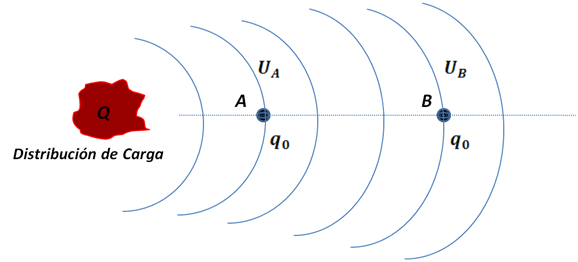
de carga eléctrica.
(Elaborada por @lorenzor)
El trabajo realizado por el campo eléctrico sobre la carga de prueba 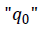 esta dado por la expresión:
esta dado por la expresión:
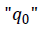 esta dado por la expresión:
esta dado por la expresión: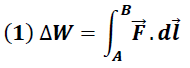
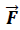 → Fuerza aplicada
→ Fuerza aplicada
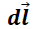 → Diferencial de desplazamiento
→ Diferencial de desplazamiento
Donde 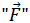 es la fuerza eléctrica debido al campo eléctrico generado por la distribución de carga y esta definido por la expresión:
es la fuerza eléctrica debido al campo eléctrico generado por la distribución de carga y esta definido por la expresión:
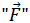 es la fuerza eléctrica debido al campo eléctrico generado por la distribución de carga y esta definido por la expresión:
es la fuerza eléctrica debido al campo eléctrico generado por la distribución de carga y esta definido por la expresión: 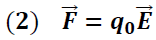
Para expresar el trabajo en función del campo eléctrico sustituimos la fuerza eléctrica dada por la expresión (2) en la ecuación (1), obteniendo:
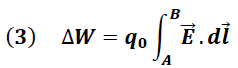
Dado que las fuerzas de Coulomb son conservativas, el trabajo realizado por esta se traduce en una disminución de la energía potencial según se expresa en la siguiente ecuación:
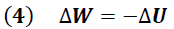
De esta forma tenemos que la variación de la energía potencial esta dada por:
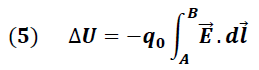
De la expresión (5) se tiene:
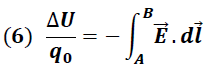
En la ecuación (6), el término
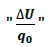 se define como la Diferencia de Potencial
se define como la Diferencia de Potencial
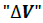 entre los puntos A y B.
entre los puntos A y B.
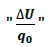 se define como la Diferencia de Potencial
se define como la Diferencia de Potencial
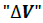 entre los puntos A y B.
entre los puntos A y B. 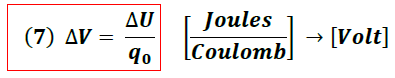
En términos del campo eléctrico, la diferencia de potencial entre los puntos A y B se expresa de la forma:
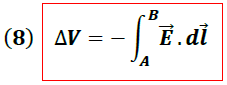
La diferencia de potencial dada por la expresión (8) es de gran relevancia en el electromagnetismo. A partir de ella podemos obtener la diferencia de potencial entre dos puntos debido a distintas distribuciones de carga.
A continuación analizaremos la diferencia de potencial entre dos puntos debido a una carga puntual (Ver figura 2).
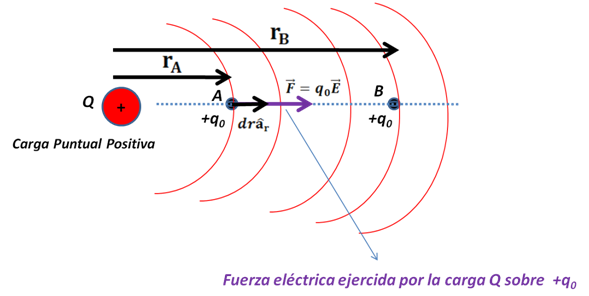
(Elaborada por @lorenzor)
Para el caso de una carga eléctrica puntual positiva
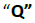 se tiene que el campo eléctrico esta dado según la Ley de Coulomb por la siguiente ecuación:
se tiene que el campo eléctrico esta dado según la Ley de Coulomb por la siguiente ecuación:
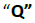 se tiene que el campo eléctrico esta dado según la Ley de Coulomb por la siguiente ecuación:
se tiene que el campo eléctrico esta dado según la Ley de Coulomb por la siguiente ecuación:
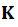 → Constante eléctrica en el vació =
→ Constante eléctrica en el vació = 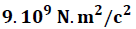
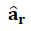 → Vector unitario en dirección radial
→ Vector unitario en dirección radial
Si sustituimos la ecuación (9) en (8), la diferencia de potencial toma la forma:
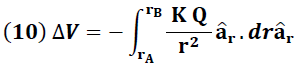
La solución de la ecuación (10) nos conduce a la expresión:
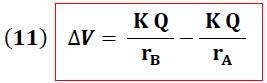
La ecuación (11) nos muestra que la diferencia de potencial entre dos puntos debido a una carga puntual es únicamente dependiente de las posiciones A y B.
Dado que:
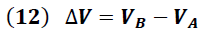
Igualando (12) y (11) tenemos:
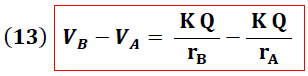
En la ecuación (13) se puede observar que el potencial eléctrico generado por la fuente de carga es directamente proporcional a la carga que genera dicho potencial e inversamente proporcional a la distancia entre la fuente de carga y el punto.
De esta forma, el potencial eléctrico en un punto
 puede generalizarse para una distribución discreta de carga (ver figura 3) a través de la siguiente expresión:
puede generalizarse para una distribución discreta de carga (ver figura 3) a través de la siguiente expresión:
 puede generalizarse para una distribución discreta de carga (ver figura 3) a través de la siguiente expresión:
puede generalizarse para una distribución discreta de carga (ver figura 3) a través de la siguiente expresión: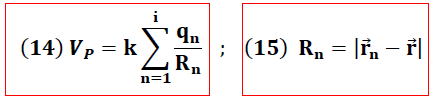
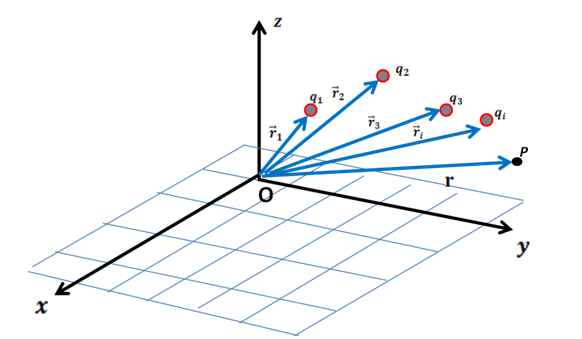
debido a una distribución discreta de carga eléctrica.
(Elaborada por @lorenzor)
Ejercicio
En el átomo de hidrógeno un protón esta separado del electrón una distancia de 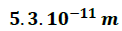 . Determine el potencial electrostático que el protón ejerce sobre el electrón a esa distancia.
. Determine el potencial electrostático que el protón ejerce sobre el electrón a esa distancia.
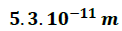 . Determine el potencial electrostático que el protón ejerce sobre el electrón a esa distancia.
. Determine el potencial electrostático que el protón ejerce sobre el electrón a esa distancia.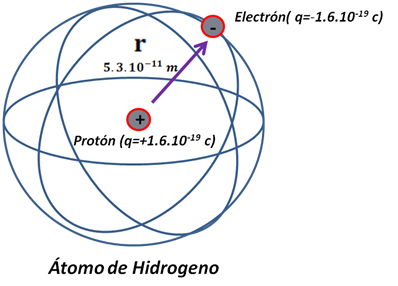
Solución
Usando la expresión (14) obtenida en nuestro análisis teórico se tiene:
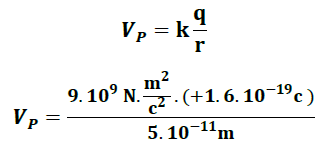
De esta forma el Potencial electrostático generado por el protón a esa distancia tiene una magnitud de:
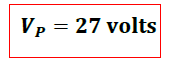
Referencias
- Introduction To Electromagnetic Fields Third Edition / Clayton R. Paul, Keith W. Whites, Syed A. Nasar
- Electrodinamica Clasica Segunda Edición / John David Jackson
- Electromagnetismo Conceptos y Aplicaciones Cuarta Edición / Stanley V. Marshall, Richard E. DuBroff, Gabriel G. Skitek
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert
¡Felicidades! Esta publicación obtuvo upvote y fue compartido por @la-colmena, un proyecto de Curación Manual para la comunidad hispana de Hive que cuenta con el respaldo de @curie.
Si te gusta el trabajo que hacemos, te invitamos a darle tu voto a este comentario y a votar como testigo por Curie.
Si quieres saber más sobre nuestro proyecto, acompáñanos en Discord: La Colmena.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Hola @lorenzor excelente tu presentación sobre potencial electrostático... De las ramas de la física el electromagnetismo es mi favorita.
Gracias por compartir tus conocimientos.
Hola saludos @hannymarchan. Gracias por tu visita y comentario. También sigo tus excelentes publicaciones.
El electromagnetismo es fascinante, también es uno de mis favorito.
Es la mejor explicacion de energia potencial electrostatica que he visto, hasta la explicacion matematica de como obtener las ecuaciones colocaste, eres el mejor :D
Saludos @dobro2020 gracias por tu visita y comentario positivo.