En primer lugar mi saludo respetuoso para toda la comunidad académica y científica de steemit, en especial a #stem-espanol, #steemstem, #utopian-io, #curie, #cervantes y #entropia, con su valioso apoyo hacemos posible nuestro crecimiento en todos los aspectos en esta prestigiosa plataforma y además nos permiten acentuar la maravillosa y constante labor de la ciencia que en muchas ocasiones nos olvidamos de su inmenso e incalculable valor para la existencia de la humanidad.

Continuamos con la temática geometría la misma que junto al lenguaje abstracto del álgebra fortalecen el extraordinario carácter analítico de las matemáticas, aspecto que hemos implementado para el análisis del esencial nexo entre la fabulosa ciencia física y las imprescindibles matemáticas. El majestuoso campo de la ciencia nos sigue guiando hacia el entendimiento de nuestro espectacular medio natural, en donde como hemos podido ver nos encontramos con cualquier tipo de fenómeno de gran influencia para nuestras vidas desde cualquier ámbito y el movimiento sin lugar a dudas representa uno de esos esenciales fenómenos para nuestra existencia.
Como hemos expresado con anterioridad el propósito principal de cada uno de estos artículos es poder identificar de forma general distintos movimientos presentes en nuestras vidas, y hasta ahora hemos conocido impresionantes tipos de movimientos tales como, el movimiento circular, parabólico, elíptico, hiperbólico, rectilíneo-curvilíneo, oscilatorio, vibratorio, ondulatorio, caótico, armónico complejo, armónico forzado amortiguado y además encontrando intrínsecamente a los fabulosos fenómenos como el movimiento periódico característico del movimiento armónico simple (M.A.S.) y el cual como hemos resaltado representa el principal fenómeno oscilatorio, lo significativo de cada uno de estos fenómenos lo constituye el gran aspecto tanto de utilidad como de vitalidad para cualquier ser viviente de este universo inclusive de este último, podríamos afirmar que cualquier partícula, cuerpo u objeto realiza cualquiera de esto fenómenos de movilidad siguiendo el lugar geométrico de alguna forma o figura que la geometría analítica ha descifrado más allá de su estructura también lo ha hecho mediante la conformación algebraica.
En el presente artículo estaremos analizando la curva cicloide y el movimiento que la misma origina al transitar por ella cualquier partícula cuerpo u objeto, pudiendo expresar de manera general que dicha curva se genera cuando un punto que se encuentra en el borde de una circunferencia gira a través de una línea recta sin resbalar en ella logrando de esta forma determinar el lugar geométrico de esta maravillosa curva.
Es importante resaltar que este tipo de curva posee propiedades fundamentales constituyendo una de ellas su longitud de arco, la cual representa 8 veces el radio de aquella circunferencia que la origina, y la otra elemental propiedad está relacionada con el área debajo de dicha curva, es decir, la que queda encerrada entre el arco que describe la cicloide y el eje de las abscisas (dentro de un plano cartesiano), esta área representa tres veces la superficie de la respectiva circunferencia creadora de la cicloide, siendo este valor calculado por 3πR2.
Se podría decir que esta curva apareció en un importante momento de nuestra historia debido a que las matemáticas estaban experimentando un desarrollo acelerado cuando dicha figura dice presente y para ese entonces se podría decir que los matemáticos de esa época fueron afortunados con la presencia de la curva cicloide ya que su utilidad se sintió para ese momento debido a que estaban en presencia de una novedosa y poderosa herramienta suministrada por la esencial ciencia de las formas y figura, es decir, la geometría analítica, dicha herramienta les permitiría estudiar y analizar propiedades de distintas curvas, tales como áreas bajo curvas, volúmenes de sólidos limitados por superficies curvas, dando paso de esta manera a una nueva área de estudio, el cálculo.
Ahora es importante referirnos al movimiento de una determinada partícula, cuerpo u objeto a través de la curva cicloide invertida, al que hemos denominado movimiento cicloidal, y para ello debemos reseñar otras dos propiedades de esta figura como lo son la braquistócrona y la tautócrona las cuales representaron para la época dos impresionantes problema para la ciencia física.
Cuando nos referimos a la braquistócrona es importante mencionar que dicha palabra se genera del griego Braquisto, el cual se refiere al más breve y Chronos, el cual significa tiempo. El problema de la braquistócrona fue planteado por el matemático suizo Johann Bernouilli en el mes de junio de 1696, este enunciado se convertiría en uno de los retos más populares de nuestra historia extendiéndole dicho reto a toda la comunidad matemática de la época, sobre todo la Europea.
El enunciado de dicho problema se enfocaba de la siguiente manera; si tenemos dos puntos uno A y otro B los cuales se encuentran situados en un determinado plano vertical, pero teniendo claro que dichos punto no se encontraban en la misma línea vertical y los mismos estaban a distintas alturas, por lo tanto Bernouilli planteaba la siguiente incógnita ¿Cuál será el lugar geométrico de la curva que debe transitar cualquier móvil que se encuentre bajo la acción gravitacional y sin presentar rozamiento, para que partiendo en un estado de reposo desde el referido punto A llegue al punto B en el menor tiempo posible?
Después de más de un año surgieron cinco soluciones, en las cuales se encontraba una del mismo Johann Bernouilli, una de su hermano Jacob Bernouilli, una de L´Hospital, de Leibniz y la de Sir Isaac Newton este último resolvió dicho problema en una sola noche, sin embargo, la solución más atractiva resulto ser la de Johann Bernouilli, para ello implementando una analogía relacionada con el principio de Fermat en donde se imaginó una esfera la cual caía por la acción gravitacional a través de un medio no homogéneo.
En relación a lo anterior dicha esfera pasaría de un medio a otro en donde los mismos (medios) tenían distintas densidades, es decir, imaginándose el espacio de caída de la esfera dividido en secciones lamínales de diferentes densidades, en donde en cada una de estas secciones la velocidad de la esfera al caer es constante, pero considerando que cada densidad de las secciones lamínales atravesadas experimentan cambios bruscos conllevando a experimentar de igual forma cambio en las velocidades de una lámina a otra, por lo que la trayectoria en cada sección laminar estará representada por un fragmento rectilíneo y que al imaginarse secciones lamínales cada vez más finas esto permitiría la construcción de una poligonal muy aproximada a una curva que para este caso resultó ser la cicloide, dando origen esta situación o solución al planteamiento el cual expresa que no siempre el camino más corto debe ser es más rápido.
Por lo tanto, gracias al aporte de cada uno de estas brillantes mentes podemos expresar que la trayectoria o lugar geométrico que nos permite ir del punto A al B empleando el menor tiempo posible es la de la curva que representa una cicloide invertida, claro siempre y cuando solo actué la acción gravitacional, ningún tipo de impulso al inicial el movimiento (en caída libre), ni existir algún tipo de rozamiento en el transitar de la respectiva bola de un punto a otro, entonces según las condiciones antes planteadas es evidente que el tiempo no es independiente de la trayectoria a seguir en la movilidad de una determinada bola u objeto.
Refiriéndonos a la propiedad de la tautócrona, dicha palabra se origina del griego Tauto la cual significa mismo, y Cronos que como ya expresamos significa tiempo, es decir, mismo tiempo, podemos expresar que dicha propiedad es la más impresionante de esta curva invertida ya que en 1973 Huygens descubre que al dejar caer una bola o determinado móvil libremente (en caída libre) desde cualquier punto siguiendo el lugar geométrico de esta curva invertida descubrió que el tiempo implementado durante dicha caída es independiente del punto de donde se soltó dicha bola o móvil.
Por lo tanto, al soltar dos bolas en caídas libres cada una siguiendo la trayectoria de una cicloide invertida observaremos que el tiempo implementado será el mismo al soltar una de las bolas al inicio de dicha curva invertida que al soltarla desde cualquier punto más debajo de la cicloide, es decir, no importará el punto de donde se inicie el movimiento para obtener el mismo intervalo de tiempo empleado por las dos bolas al llegar al punto final, claro teniendo en cuenta las condiciones iniciales antes descritas y las características similares entre las dos bolas o móviles involucrados.
Tal acción podemos determinarla por el hecho de ser la pendiente de dicha curva más inclinada en sus extremos y al salir desde el extremo superior el móvil podrá alcanzar mayor velocidad en un intervalo de tiempo menor, es decir, obtendrá mayor aceleración, pero cuando partimos de cualquier punto más abajo la velocidad será afectada por el menor espacio a recorrer y la capacidad para acelerar será menor por lo que hace que el móvil se desplace más lento en relación con aquel que partió desde el punto inicial o extremo superior de dicha curva invertida.

Seguimos obteniendo de la espectacular ciencia de las formas y las figuras, es decir, geométrica analítica todos aquellos lugares geométricos por donde transitan innumerables partículas, cuerpos u objetos al describir algún tipo de movimiento tal y como hemos visto en los anteriores artículos, en donde encontramos trayectorias vinculadas a reconocidas e importantes figuras geométricas como la línea recta y su movimiento rectilíneo, la circunferencia y su movimiento circular, la parábola y su movimiento parabólico, la elipse y su movimiento elíptico, la hipérbola y su movimiento hiperbólico, combinación de estas figuras o alguna porción de ellas como el movimiento rectilíneo-curvilíneo, oscilatorio, vibratorio, ondulatorio, así como otras figuras complejas como la mariposa o atractor de Lorentz en un movimiento caótico, también mediante la combinación de curvas periódicas o armónicas dando origen a trayectorias complejas como las denominadas figuras de Lissajous esencialmente producidas por la composición de dos movimientos armónicos simples (M.A.S.) de direcciones perpendiculares entre sí.
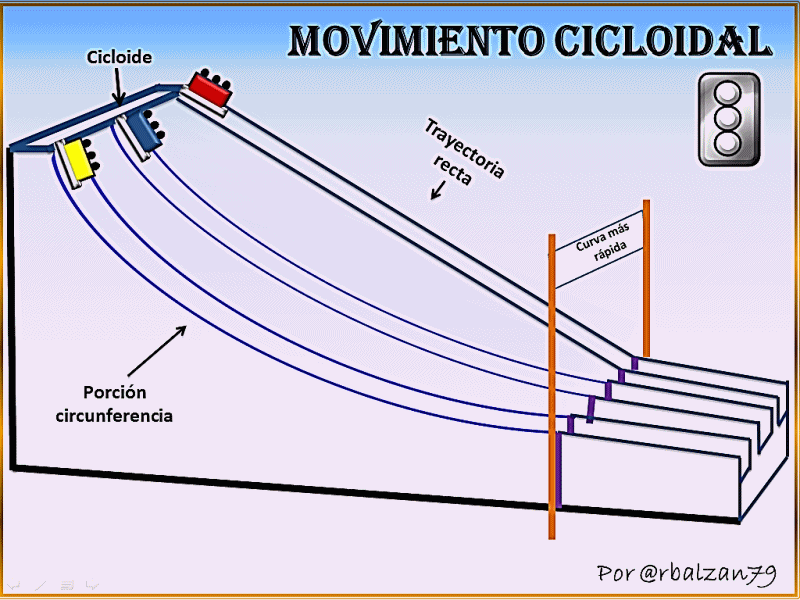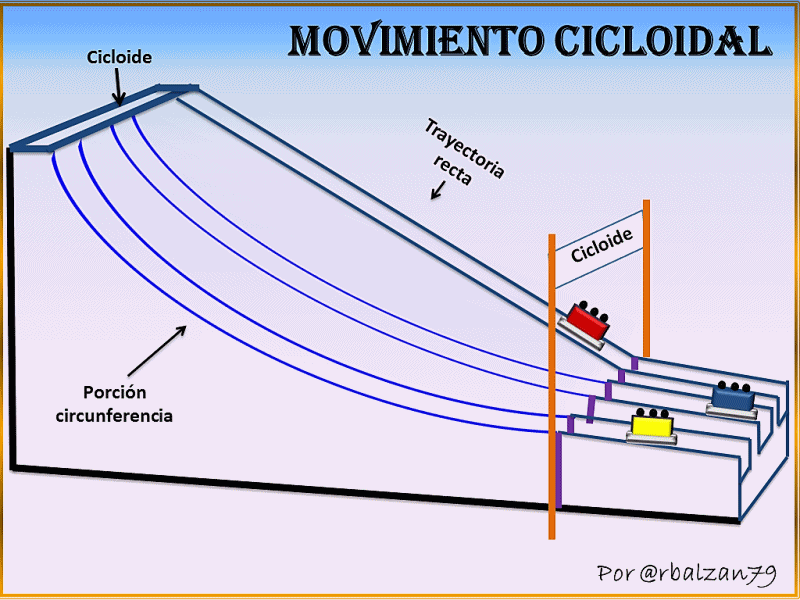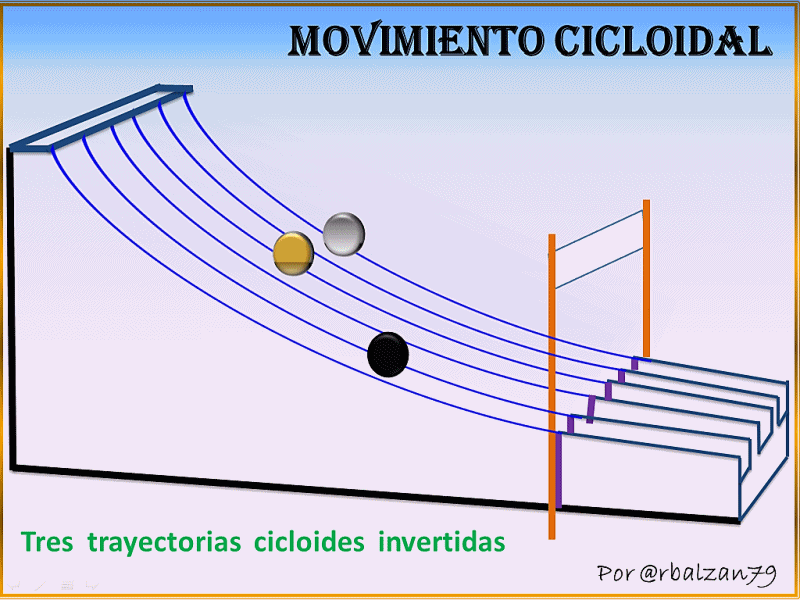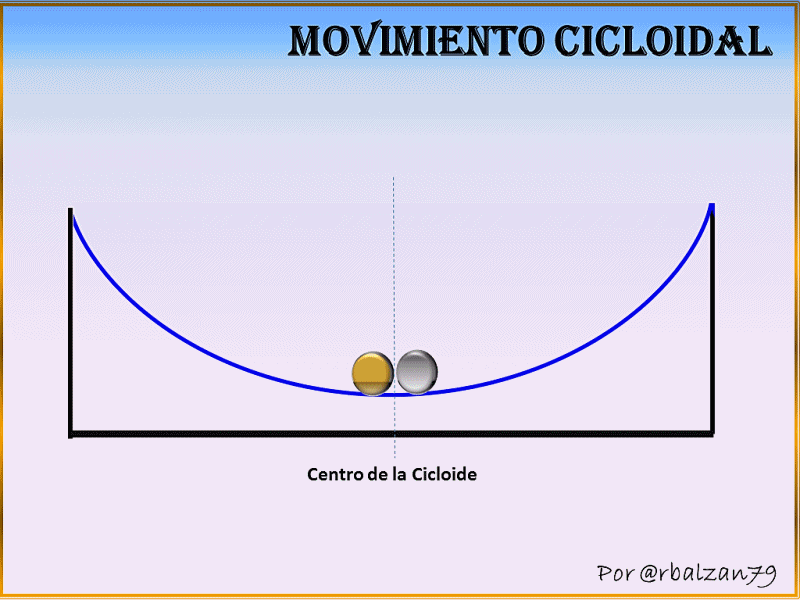
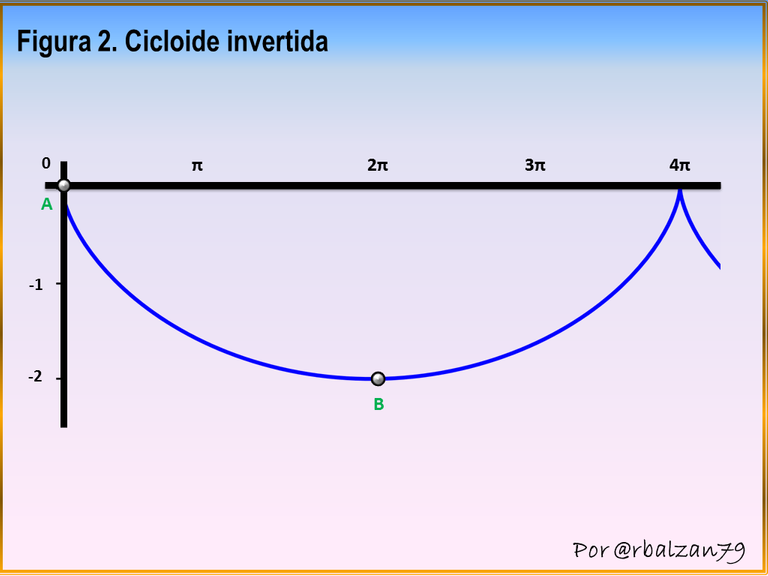
En esta oportunidad nos encontramos con una extraordinaria curva o figura la cual nos permite ir de un punto a otro en el menor tiempo posible bajo ciertas condiciones iniciales antes descritas con relación a la gravedad, impulso inicial y rozamiento, esta impresionante figura es la denominada cicloide invertida, dicha figura original podemos decir que es generada por un punto fijo anclado a una circunferencia la cual rota sin deslizarse sobre una línea recta como la representada por el eje de las abscisas (X) de un plano cartesiano, como podemos observar en la siguiente figura 1.

Ahora observaremos un gif animado con la finalidad de poder apreciar con mayor detalle el movimiento de la circunferencia junto al punto generador de la curva cicloide.

En el anterior gif notamos como se origina el lugar geométrico de una curva cicloide, figura que al invertirla encontramos la curva que en caída libre bajo ciertas condiciones iniciales de cero empuje, bajo la acción gravitacional y sin rozamiento un móvil puede recorrer tal espacio geométrico en menor tiempo que al transitar cualquier otras curvas incluso una recta, en la figura 2 mostraremos la cicloide invertida.
Impresionantes son las figuras utilizadas por la geometría analítica para lograr conectarse con el entendimiento de cualquier fenómeno presente en nuestro entorno como las que observamos en las anteriores figuras en donde una determinada partícula, cuerpo u objeto puede llevar a cabo un movimiento cicloidal.

# Movimiento Cicloidal
El movimiento cicloidal, fenómeno característico debido a la movilidad de alguna partícula, cuerpo u objeto (móvil) a través de la curva llamada cicloide invertida y la misma representa el lugar geométrico que describe un determinado punto (P) el cual se encuentra situado de manera constante (mientras describe dicha curva) en el borde de una circunferencia de radio (r) la cual gira o da vueltas sobre una línea recta sin resbalar o deslizarse en ella, esto lo realiza a una velocidad constante hasta que dicho punto (P) logre alcanzar la posición cuyas coordenadas sean de (2πR, 0) , es decir, en palabras más sencillas es cuando dicha circunferencia alcance a realizar una vuelta completa tomando en cuenta el punto (P) como referencia.
Para el análisis del movimiento cicloidal de alguna partícula, cuerpo u objeto debemos siempre tomar en cuenta las importantes propiedades antes mencionadas como la Braquistócrona y la Tautócrona ya que dichas cualidades ofrecen particulares e impresionantes características de movilidad a un determinado móvil el cual describe el lugar geométrico de una cicloide invertida.
Para la propiedad Braquistócrona recordemos el enunciado que realizara el matemático Johann Bernouilli el cual se enfocaba en dos puntos (A y B) situados en un mismo plano pero no en la misma recta vertical y a diferentes alturas, en donde se planteó la siguiente pregunta ¿Cuál sería aquel lugar geométrico que representaría la curva por la cual debería trasladarse un determinado móvil el cual encontrándose bajo la acción de la gravedad, sin rozamiento alguno durante su recorrido y que partiendo de un estado en reposo desde A hasta el punto B, dicho móvil requiera el menor tiempo posible?
Este planteamiento permitió dar origen al fenómeno que conocemos hoy como movimiento cicloidal debido a que el lugar geométrico de esta curva resultó ser la de la figura que actualmente denominamos cicloide invertida, y por tanto el movimiento que a través de ella se lleva a cabo lo conocemos como cicloidal, un claro ejemplo lo representa el gif animado al inicio de esta publicación ya en el mismo podemos observar tres trayectorias, es decir, recta, porción circular y cicloide invertida, resultando la curva cicloide invertida la de menor tiempo para ser recorrida, todo esto bajo las condiciones iniciales ya mencionadas ( caída libre, bajo la acción de la gravedad y sin rozamiento) para las tres trayectorias, de esta manera podemos afirmar entonces que el trayecto más corto no implica que sea el más rápido.
Para consolidar la idea anterior debemos tener presente desde el punto de vista de la cinemática, cuando analizamos la caída libre de una determinada bola (móvil) partiendo de un punto cualesquiera como A hacia otro punto como B y ambos puntos encontrándose en un mismo plano pero no en la misma línea vertical como lo hemos expresado con anterioridad, según la Ley de la conservación de la Energía, tenemos que en cada instante de la trayectoria seguida por dicha bola la suma de sus energías potenciales y cinética será constante.
Que podríamos decir sobre el tiempo implementado por la bola desde A hasta B ¿Es mismo es independiente de la trayectoria recorrida? Claramente sabemos que el espacio o lugar geométrico transitado desde A hasta B será mínimo si dicha figura es una línea recta, pero esto no garantiza que sea la trayectoria con el menor tiempo empleado, como lo pudieron demostrar los grandes personajes históricos antes descritos, en donde según las condiciones antes planteadas es evidente que el tiempo no es independiente de la trayectoria a seguir en la movilidad de una determinada bola u objeto.
Al referirnos a la otra propiedad, es decir, la tautócrona, podemos expresar que desde el punto de vista de movilidad es impresionante la característica aportada a un determinado móvil al recorrer una cicloide invertida, sobre todo al tiempo implementado por cualquier partícula, cuerpo u objeto, ya que como descubre Huygens cuando al dejar caer libremente un determinado móvil sin importar el punto de salida de este, el tiempo implementado será el mismo al punto de llegada, es decir, independientemente de la altura de donde se suelta o deja caer el móvil el tiempo invertido por dicho móvil será siempre el mismo al llegar al extremo final de la trayectoria de la cicloide invertida.

Los modelos matemáticos nos han brindado el abstracto lenguaje necesario para el acercamiento a nuestra naturaleza, es decir, lograr la mayor simplificación posible de nuestro entorno y reducir la enorme complejidad de nuestro majestuoso universo, representando un claro ejemplo de utilidad de estos modelos el estudio del fenómeno del movimiento realizado por la ciencia física a través de la cinemática con la ayuda de las matemáticas y su geometría analítica.
Para la determinación de las ecuación de un punto cualesquiera P(x,y) de un circunferencia que gira sobre una línea recta como el eje de las X de un plano cartesiano utilizaremos la figura 1, por lo tanto tenemos:

Por lo tanto, el ángulo conformado entre el segmento vertical el cual pasa por el centro de dicha circunferencia (C) y además perpendicular al eje de las X y con radio (r) se encuentra en los intervalos 0≤ β ≥ 2π, y cuando β = 0 tendremos que el punto (P) coincide con B.
Para las ecuaciones que determinan el vector velocidad podemos obtenerlas al derivar las formulaciones que determina el vector posición de un determinado punto (P) con respecto al tiempo por lo tanto tenemos:

En las anteriores ecuaciones 3 y 4 notamos que la primera derivada de una ecuación posición con respecto al tiempo representa la velocidad ya que la misma constituye un cambio de una determinada partícula, cuerpo u objeto que transita por una determinada trayectoria como la cicloide en este caso.

Continuamos con la identificación de los distintos fenómenos de movilidad presentes en nuestro entorno y los cuales como los otros fenómenos estudiados transitan por innumerables trayectorias que las hacen características a sus respectivos nombres como es el caso de la fabulosa trayectoria de la cicloide invertida y el movimiento que genera el cicloidal.
Esta impresionante curva muchos las denominaron la Helena de la geometría (Helena de Troya de la mitología griega) o de las curvas y pudiéramos decir que tal nombre fue otorgado por su belleza o simplemente por las polémicas que la mismo produjo durante su desarrollo, en sus inicio dicha curva representó una gran herramienta aportada por la geometría analítica para profundizar en muchos aspectos de las matemáticas ya que dicha herramienta les permitió poder estudiar y analizar importantes propiedades de diferentes curvas, tales como áreas debajo de ellas, volúmenes de sólidos los cuales estaban limitados por superficies curvas, permitiendo de esta manera poder abrir camino a una nuevo espacio de estudio como el cálculo infinitesimal.
La cicloide ese espacio geométrico generado por un determinado punto de una circunferencia que gira o da vueltas sobre una línea recta sin resbalar o deslizar a velocidad constante, durante su desarrollo o descubrimiento importantes científicos de nuestra historia como Johann Bernouilli, Jacob Bernouilli, L´Hospital, Leibniz y Sir Isaac Newton pudieron conocer y resaltar las impresionantes cualidades de dicha figura encontrándose propiedades increíbles como la Braquistócrona y la Tautócrona mediante una cicloide invertida.
Con la cicloide invertida pudimos notar que la misma representa el lugar o espacio geométrico más rápido para transitar desde un determinado punto de partida (A) hasta un punto de llegada (B) los cuales se pudiesen encontrar en un mismo plano pero no en la misma línea vertical y a diferentes alturas, tomando en cuenta ciertas condiciones iniciales para el móvil tales como dejarlo caer en caída libre (sin empuje), bajo los efecto de la acción gravitacional y sin ningún tipo de rozamiento durante todo el recorrido, lo cual el gif al principio de la publicación representa un ejemplo comparativo con el desplazamiento de un móvil tanto por un trayectoria cicloide como por una recta o porción de una circunferencia, resaltando de esta forma la propiedad Braquistócrona de la cicloide invertida.
Pero también pudimos observar la propiedad Tautócrona de dicha figura invertida ya que la misma permite un periodo de tiempo igual para un móvil que inicie el recorrido desde el extremo más alto de la curva como para aquel que inicia el recorrido más abajo que el primer móvil hasta llegar al final del recorrido e incluso al soltar dos móvil en sentido opuesto uno más arriba que el otro ambos se encontraran exactamente en el centro de la curva al mismo tiempo.
En conclusión si soltamos tres móviles en caída libre siguiendo trayectorias diferentes la curva cicloide invertida será recorrida en menor tiempo, si soltamos estos tres móviles a distintas alturas iniciales cada uno siguiendo una cicloide invertida tomarán el mismo tiempo en llegar al punto final de dicha curva, de igual manera si soltamos dos móviles en sentido opuesto y también a diferente altura siguiendo la trayectoria de una cicloide invertida ambos se encontraran exactamente en el centro de dicha curva.
Para concluir mis amigos lectores, los distintos fenómenos de movimiento sean de cualquier índole particular o compuestos (complejos) estarán por siempre con nosotros permitiéndonos y brindándonos una mayor estabilidad social y por supuesto gracias a ciencias como la cinemática y la geometría analítica podemos reafirmar que cada vez estamos más cerca de nuestro medio natural o entorno.
Hasta otra oportunidad mis apreciados lectores de steemit, en especial a los miembros de la gran comunidad de #STEM-Espanol, los cuales reciben el apoyo de otras tres grandes comunidades como los son #steemstem, #utopian-io y #curie, por lo cual recomiendo ampliamente formar parte de este hermoso proyecto, ya que resalta la valiosa labor de la academia y del campo científico, pero sobre todo, por el gran respecto, dedicación y ayuda para sus miembros.
Nota: Todas las imágenes fueron elaboradas usando las aplicaciones Paint, Power Point y el gif animado al principio de la publicación fue elaborado con la aplicación de PhotoScape y el gif animado, lugar geométrico de la cicloide fue desarrollado con la aplicación de GeoGebra.

[1] Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.
[2] Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.
[3] Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.
[4] Raymod A. Serway y John W. Jewett, Jr. Ed. Thomson. Física. Edición 1 y 3.
[5] Giancoli, D.C. Física, principios y aplicaciones, Reverté S.A. España, 1985.
[6] Casasco Juan Patricio, Valoni Andres, Romani Julieta. Cicloide. Universidad Favaloro. Julio 2001.
[7] Arriagada Sandoval Camila. Modelos Matemáticos. Universidad del BÍO-BÍO. Chillan, 2015.
[8] Prieto Santiago, Rodríguez, Silveira Ismael. Física General 1. Universidad de la República; Instituto de física, Facultad de ingeniería - UdelaR, 2007.
[9] Lafuente J. Geometría diferencial de curvas en el plano. Enero de 1998.
Gracias por su valioso apoyo, saludos a toda la comunidad de cervantes.
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @utopian-io.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness and utopian-io witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having added @steemstem as a beneficiary to your post. This granted you a stronger support from SteemSTEM.
Thanks for having used the steemstem.io app. You got a stronger support!
Thanks to the communities of @SteemSTEM, @utopian-io and @curie for the support received.
Congratulations @rbalzan79! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPVote for @Steemitboard as a witness to get one more award and increased upvotes!
Hi @rbalzan79!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thanks to the great community of @utopian-io for their valuable support. Greetings