El objetivo persistente de la matemática en nuestras vidas.
El transporte del conocimiento matemático después de una buena dosis de argumentación teórica.
La esencia pura y de naturaleza matemática más allá de cualquier hallazgo que la refuerce.
De seguro que esta visión tendrá un gran recibimiento por parte de una parte de la sociedad que valora las cualidades humanas basadas en la filosofía existencial de todo lo que sirve a la humanidad para su desarrollo, para nadie es un secreto que la matemática ha sido fuente de desarrollo para generar grandes inventos e ir paulatinamente en un crecimiento en lo que a tecnología y ciencia se refiere. Es por ello que verle otra cara distinta a la matemática resulta de gran valor, ya que en su análisis filosofal de seguro encontraremos otros argumentos no encontrados en su forma tradicional de entenderla y comprenderla en su naturaleza misma.
Si apartamos los asuntos de estudios que existen en la filosofía con los asuntos matemáticos, seguramente bajo una nueva visión más teórica podremos encontrar los vínculos exactos que conecten a la filosofía con la matemática en un solo bloque que genera una visión innovadora y revolucionaria. Resulta que estos vínculos en mi modo de pensar en las cosas que necesitan la uno de la otra, me hacen referirme en un sentido irreversible donde la filosofía al igual que muchas cosas de este mundo siempre van a necesitar de la matemática, y en contraparte todo el conocimiento tal y como lo hemos conocido a través de la historia de la humanidad siempre va a necesitar de la filosofía como la madre de todas las ciencias.
La forma en cómo investigan los matemáticos para trabajar y aportar cada vez más en esta grandiosa disciplina nos hace pensar en que realmente en vez de que se conjuguen elementos que la separen, existen cada vez más argumentos que las hacen complementarias una de la otra. Entendamos esta forma de trabajo de los matemáticos, cuando ellos se ocupan de los fundamentos básicos y en desarrollo de esta disciplina entran en un proceso de investigación fundamentada, ya que primordial es que se desarrollan y se sienten las bases o premisas en las que esta se sustenta.
Ahora vamos a su contraparte, que ocurre cuando los filósofos trabajan en el pensamiento que encierra el enigma de la filosofía oculta dentro de los saberes matemáticos, pudiéramos estar ante la presencia de un aporte filosófico dentro de las matemáticas como disciplina sobre la que quizás muy poco se discuta y analice. Todos estos posible enlaces que de por sí ya son existentes, nos llevaría y a la suprema interacción que pueda existir entre filósofos y matemáticos, esta interacción de seguro reforzará las bases existentes que estudian las cuestiones relativas a la naturaleza de las matemáticas.

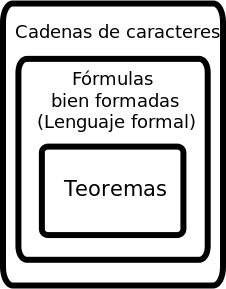
Recuerdo mis años de estudiante en la Universidad, al principio de mis estudios universitarios me llamo mucho la atención como la geometría Euclidiana contemplaba un conjunto de postulados teóricos, algunos más abstractos que otros, pero con una singularidad particular, y es que de este conjunto de postulados que sustentan la geometría Euclidiana solo los teoremas representan enunciados que pueden ser demostrados pero a partir de que se citen otros postulados que no requieren de demostraciones como es el caso de los axiomas de incidencia, en el que se consideran verdaderos sin requerir de demostración ya que en ellos se revela la naturaleza de la existencia misma basada en las fundamentaciones de la lógica matemática.
Hoy en día puedo reflexionar acerca de aquello que me impactó referente a esa abstracta argumentación teórica en la que se fundamentaban los cimientos de la Geometría Euclidiana, por lo que con propiedad puedo afirmar hoy en día que para poder entender algo más allá de una serie de cálculos matemáticos, tenemos que antes podernos nutrir de esa parte filosófica que encierra la matemática en todas sus formas, sean algebraicas, aritméticas, geométricas hasta alcanzar lo más profundos avances del cálculo infinitesimal.
¿Qué llamo la atención de los filósofos de la antigüedad en lo que concierne a la estructura y modelo de la matemática?
No son todos los aspectos que soportan a la matemática que fueron de interés para los filósofos de la antigüedad, pero sí algunos que se soportan en cuestiones que son netamente del razonamiento y pensamiento humano. Existe un camino, una vía de acceso que enamora y apasiona al filósofo a seguir los rastros de ciertos aspectos matemáticos como el dinamismo interno de la naturaleza del pensamiento matemático, entendiéndose así a esta forma dinámica intrínseca en cimientos matemáticos como la lógica, ahora bien y por qué interesa el estudio de la lógica a los filósofos, muy simple, tan solo por el hecho de que la lógica dentro de su estructura interna lleva implícito una forma simple, sobria y clara de aceptar la existencia de lo inexplicable.
Los filósofos arrastrados por esa inquietante forma de querer aclarar los misterios del conocimiento humano, han visto en el pensamiento matemático una forma ideal para poner a prueba sus hipótesis y teorías filosóficas. Sin embargo en este camino en el que la filosofía siempre busca de esa parte de la matemática lo que la pueda ayudar a fundamentar cada vez más sus teorías, se debe ir más lejos, por lo que puede llegar a plantear el hecho de que las matemáticas son algo más profundo y entendible que el simple fundamento del quehacer científico, por lo que las matemáticas representan un fuerte enlace de nutrición al conocimiento filosófico.
Ejercicios de autoanálisis y reflexión mediante interrogantes planteadas acerca de la vinculación de la matemática filosófica
1. ¿Cómo podemos reflexionar en el modo estructural de los objetos matemáticos desde un enfoque de la filosofía matemática?
El carácter y esencia de los teoremas dentro de la matemática nos ayuda a responder esta interrogante, ya que el objetivo filosófico dentro de la matemática está en poder demostrar todo lo que pregona, sin embargo también que valerse de ciertas premisas antagónicas a la demostración, tal es el caso de los axiomas, estos postulados se tienen que considerar verdad sin requerir de demostración ya que forman parte de la médula espinal de todo lo que se conoce.
2. ¿Cuál es la verdad matemática?
La verdad matemática encierra todo lo concerniente a la epistemología de la matemática, dentro de este rango de saberes se puede discutir sobre las necesidades humanas que llevaron a desarrollar el conocimiento matemático primitivo para ir pasando por distintos procesos evolutivos hasta llegar al conocimiento actual que hoy en día conocemos. La naturaleza humana juega un papel primordial en la verdad matemática, ya que uno de los proceso empíricos que presumimos siempre ha existido es el de la necesidad de contar.
3. ¿Existe alguna relación entre lo abstracto de la matemáticas y la realidad?
Realmente lo abstracto surge en sa imposibilidad existente de conseguir dar respuesta a ciertas cosas de la vida, por lo que aunque muy abstracto que parezcan ciertos postulados, siempre existirá una relación entre lo externo (universo material) y los fundamentos abstractos de la matemática. Lo que nos lleva a concluir cada vez más que la forma en la que se puede moldear lo abstracto dependerá del aporte que le brinde la filosofía a esta forma de ver la realidad matemática.
4. ¿Cómo es posible encontrar el vínculo existente para que ciertos elementos como el punto, la recta, el plano, infinito y el número puedan trascender más allá del ámbito simplemente matemático?
Al principio necesario era sentar las bases de un todo como un conjunto universal de elementos o premisas que iban a significar la base de la matemática moderna, pero no era sino con el aporte de grandes filósofos y matemáticos que se empezó a materializar todo este conocimiento matemático en aplicaciones que involucraría otras ciencias como la física, química y otras ramas de las ciencias naturales. Todavía en el campo de las aplicaciones resulta muy importante un enfoque filosófico para no perder el horizonte sobre ese pensamiento que nos lleva a reflexionar sobre esas necesidades básicas que nos llevan a seguir innovando, creando e inventando matemática, y para eso debemos filosofar sobre estos asuntos tan esenciales y base sobre todo el conocimiento tal y como lo conocemos en la actualidad.
Conclusiones y aportes
Si lográramos encerrar todo este proceso que vincula la matemática y la filosofía dentro de un conjunto de elementos que resulten necesario para la convergencia filosófica de la matemática, de seguro que tuviéramos que estudiar el análisis de los siguientes elementos:
Formalismo: para todos es bien sabido que cuando se trata de estudiar y comprender algún tópico matemático existe una estructura formal para dar a conocer algún postulado en forma de corolario, teorema o axioma, e incluso la forma en la que se va a demostrar determinado teorema lleva implícito un proceso formal. Esta forma formal quizás puede resultar de interés para ser adoptada por los estudios de la filosofía.
Proceso de deducción: Existe una forma idealmente formal que va llevándonos a una serie de pasos donde la deducción hacia otros puntos y formas nos ayuda a demostrar algún postulado, son símbolos como los de implica, simbología de conjuntos, el infinito y otros símbolos más que nos van ayudando a ese proceso de deducción, en lo referente al pensamiento humano y la filosofía misma también adopta una forma deducción para ir acomodando sus ideas y estructuras en la transmisión del conocimiento.
La intuición: este proceso ha ayudado mucho al avance del conocimiento matemático, podemos citar por ejemplo una forma de entender la teoría de Límite y continuidad de una función real, existen conceptos más abstractos, tal es el caso del concepto formal de límite, el cual involucra una serie de procesos deductivos bastantes complejos, no es hasta este punto donde la intuición nos ayuda a entender un concepto que a mi parecer es más innovador como es el caso de la intuitiva de límite de una función de variable real.

Existe otros elementos más que en conjunto ayudan a dar una formalidad de vinculación entre la filosofía y la matemática, lo otro importante es mencionar que la búsqueda constante de la filosofía encerrada en la matemática es la punta de lanza para desarrollar nuevos postulados más entendibles sin perder ese horizonte formal, deductivo e intuitivo que encierra el estudio y aplicación de la matemática en uno de los elementos más atractivos para la existencia y desarrollo humano.
Bibliografía consultada y recomendada
[1] Filosofía y Matemáticas. M de Guzmán.
Envíanos un mensaje en Discord 😍🤗❤
https://discord.gg/vzHFNd6
$trdo
!giphy wine
giphy is supported by witness untersatz!
Congratulations @pandaparker, you successfuly trended the post shared by @carlos84!
@carlos84 will receive 0.15880050 TRDO & @pandaparker will get 0.10586700 TRDO curation in 3 Days from Post Created Date!
"Call TRDO, Your Comment Worth Something!"
To view or trade TRDO go to steem-engine.com
Join TRDO Discord Channel or Join TRDO Web Site
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Te informamos que el PROYECTO ENTROPÍA ha creado un nuevo servicio, la Creación de cuentas nuevas de Steemit, para más información puedes visitar este enlace.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Gracias por el apoyo amigos de @entropia. Saludos
Gracias por el apoyo a @alexa.ciencias y al equipo de HispanoHablantes. Saludos
Congratulations @carlos84, your post successfully recieved 0.1588005 TRDO from below listed TRENDO callers:
To view or trade TRDO go to steem-engine.com
Join TRDO Discord Channel or Join TRDO Web Site
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider using the steemstem.io app and/or including @steemstem in the list of beneficiaries of this post. This could yield a stronger support from SteemSTEM.
Envíanos un mensaje en Discord 😍🤗❤
https://discord.gg/vzHFNd6