
Operaciones matemáticas limitadas
Cuando realizamos las cuentas numéricas en las operaciones matemáticas nos podemos encontrar con algunos pasos que no son tan sencillos de resolver si no contamos con los conocimientos sólidos en Los Fundamentos Matemáticos
Cada día vamos a encontrarnos frente a retos novedosos, nuevos problemas y cuando aparezcan debemos estar preparados para afrontarlos, identificando los elementos que lo componen y su relación con el tiempo de origen y rapidez para encontrar una solución, por más pequeño que sean los procedimientos a aplicar, siempre debemos tener una estrategia para comenzar a manejar el problema de la mejor manera. Me refiero al tema de enseñanza-aprendizaje con las bases matemáticas que nos permitan implementar un plan y mejorarlo con la práctica, y aquí les presentaré algunos ejemplos donde se deben considerar algunas restricciones o condiciones para que el resultado o solución hallada tenga algún sentido útil y pueda ser aplicado de manera concreta en un problema matemático.
Frecuentemente usamos las operaciones aritméticas (números y valores) y algebraicas (letras y cantidades) para trabajar los distintos tipos de funciones y en algunos casos se generaliza con la frase "X representa todos los valores", lo cual puede resultar inválido cuando existe una división entre 0, f(X) = 1/X , por lo que la restricción sería que X ≠ 0

Restricción para la División
Todos los problemas matemáticos tienen una solución, pero debemos analizarlo y proponer una respuesta basada en conocimientos científicos y no en la aplicación "mecánica" de una metodología que nos lleve a una incoherencia matemática. Veamos en el siguiente ejemplo que la notación para la División en el conjunto de los números reales (ℝ) no se cumple al 100%, existiendo al menos la siguiente restricción:
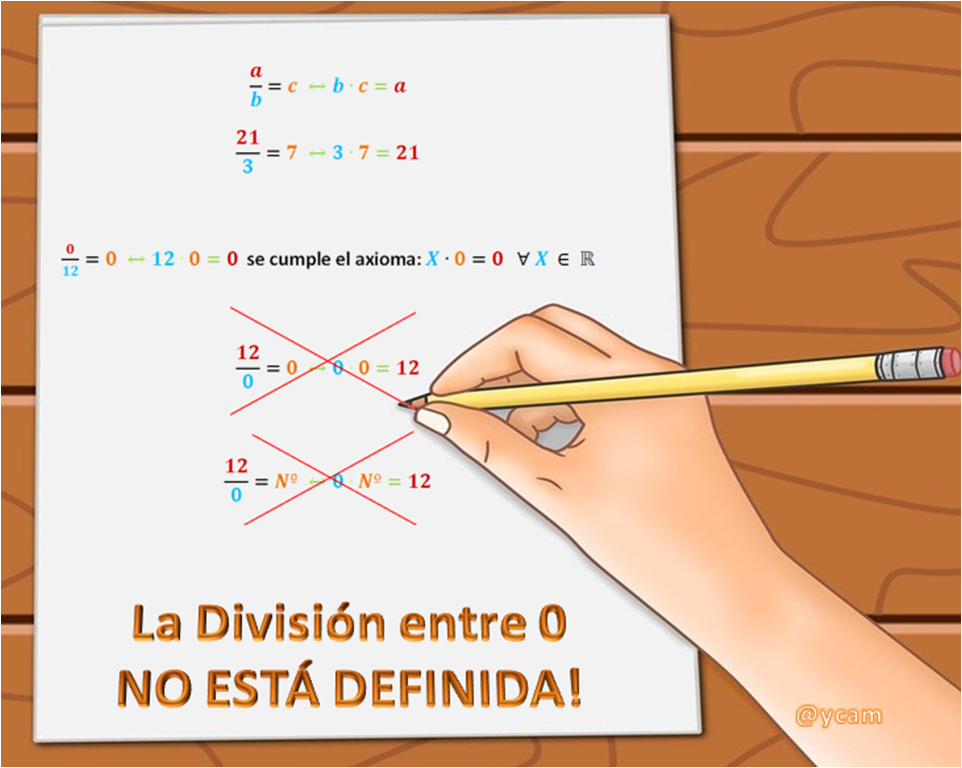
Esta restricción presentada en el axioma nos indica que el 0 no tiene inverso en la multiplicación y que la División se puede realizar siempre y cuando el "denominador" sea distinto de cero!
Como no está definida la División, podemos proceder a analizarla como una función f(X) = 1/X y estudiar su tendencia cuando nos aproximamos a 0

Funciones exponenciales
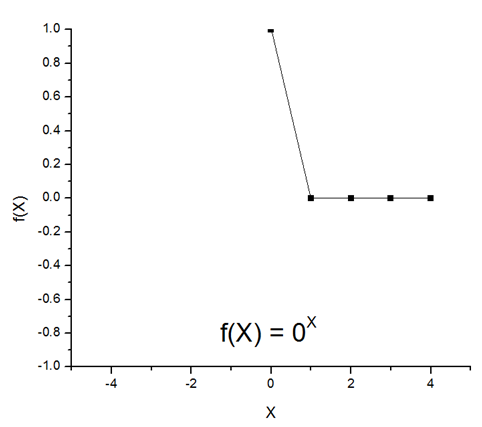
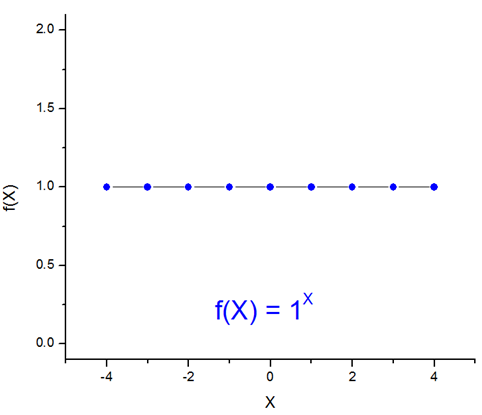
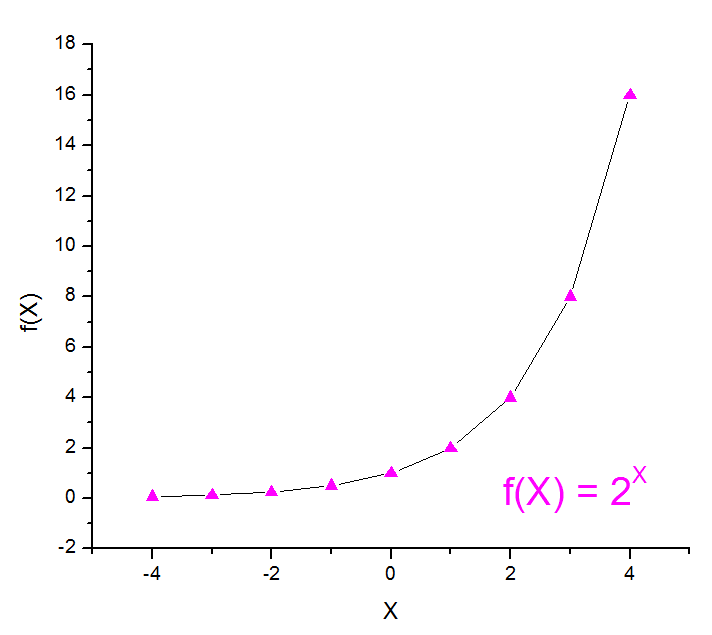
La función está restringida para valores de a > 0 y a ≠ 1
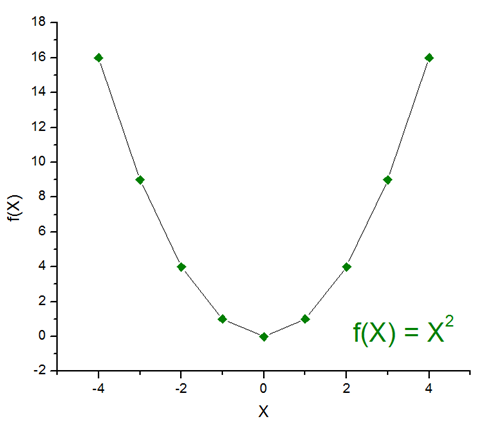
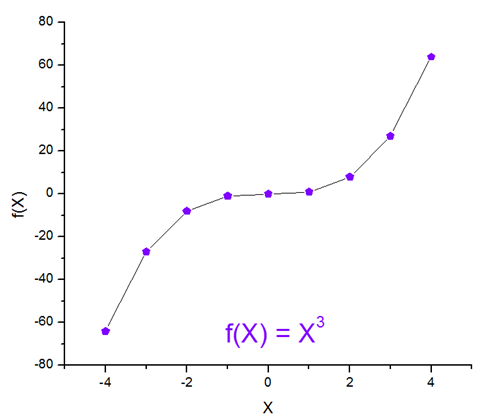
Para la función cuadrática, f(x) ≥ 0, siempre va a dar valores positivos, mientras que si el exponente es 3, tenemos alternadas las imágenes positivas y negativas, por lo que no tendría sometimiento a restricciones:
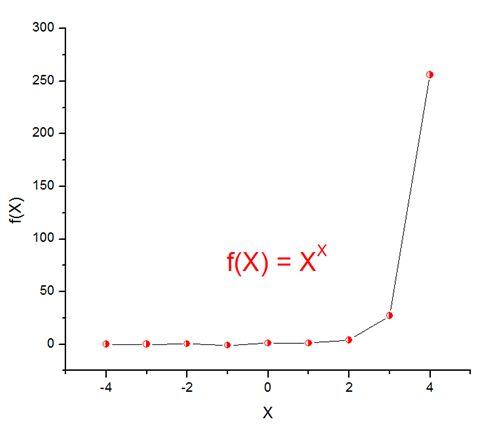
También podemos observar la tendencia de la función f(X) = XX a incrementarse a medida que aumenta X+ y alterna valores positivos y negativos para X < 0.
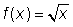 donde se debe cumplir que x ≥ 0, porque la raíz cuadrada de un número negativo no existe o se le llama imaginario!
La restricción de una potencia de una potencia, (an)m = an∙m, entonces debemos tener presente que a ≥ 0, porque si a es negativo (a < 0) y además aparece una raíz de índice par, entonces me remitiré al párrafo anterior y no se puede resolver.
donde se debe cumplir que x ≥ 0, porque la raíz cuadrada de un número negativo no existe o se le llama imaginario!
La restricción de una potencia de una potencia, (an)m = an∙m, entonces debemos tener presente que a ≥ 0, porque si a es negativo (a < 0) y además aparece una raíz de índice par, entonces me remitiré al párrafo anterior y no se puede resolver.
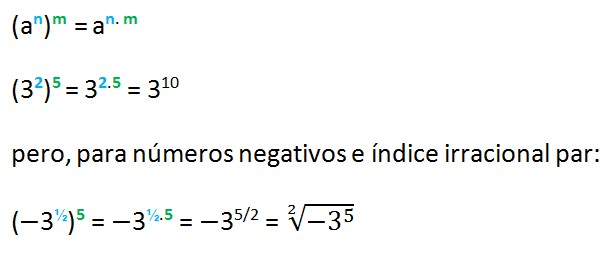
Apoyo bibliográfico y fuente de imágenes
Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
- Nota de discusión: No es posible dividir entre cero
- Imagen de Jorgeduardo: Profesora
- Imagen de Jorgeduardo: Profesora y pizarra
- Dibujo de Jorgeduardo: Papel sobre madera
- Wikipedia: Fundamentos de Matemáticas
- Video: Restricciones de funciones irracionales
Reflexión
A pesar de los problemas que se nos presenten y la dificultad que puedan aparentar, todo el conocimiento en Matemática será capas de superarlo con las herramientas y procedimientos adecuados

Me hiciste recordar mis clases de cálculo en la universidad. Que complicado puede ser entender límites al inicio y que bien lo has descrito aquí. Gracias por traer este tipo de conocimientos a la blockchain. Ojalá que sea muy bien apreciado por estudiantes alrededor del mundo.
Cálculo I y Cálculo II, no se olvidan tan fácil esas nociones matemáticas que producían un choque mental con las bases matemáticas que traíamos del colegio. Gracias por leerme!
Es así!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Congratulations @ycam! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
Your next target is to reach 10000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz: