Antes de desarrollar el tema a tratar vamos a hablar de algunas expresiones matemáticas con resultados que parecen exagerados.
Veamos por ejemplo, la expresión siguiente: 1/x y hagamos que el denominador x se haga cada más cercano a cero tanto por la derecha como por la izquierda.
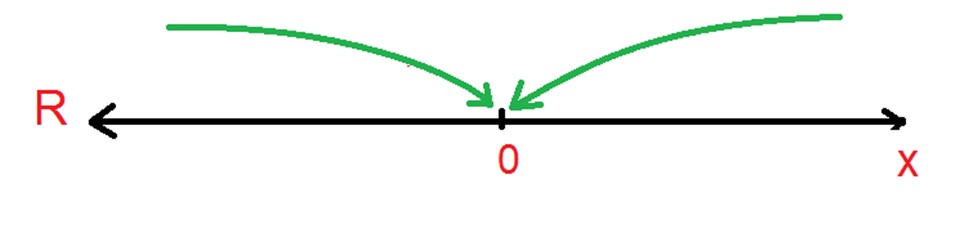
Haciendo una pequeña tabla nos vamos a dar cuenta de que cuando x se hace cercano a 0 por la derecha, esto es, a través de valores positivos, el resultado de 1/x se hace arbitrariamente grande, veamos en este cuadro, parte de los resultados:
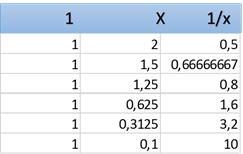
Si continuamos dándole valores a x cada vez más cercanos a 0 por la derecha, como por ejemplo: 0,01, 0,001, 0,0001, 0,00001…; estaríamos en proceso infinito durante el cual los valores de 1/x se harían cada vez más infinitamente grandes. Veamos algunos de esos valores completando la tabla anterior:
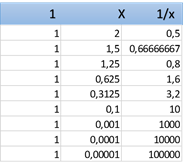
Pienso, que todos estaremos de acuerdo en afirmar que a medida que x decrece, es decir, se hace infinitamente pequeña, ocurre lo contrario con 1/x; se ve claramente, que en este proceso de decrecimiento de x, 1/x se hace infinitamente grande.
Ahora hagamos algo similar por la izquierda de 0, es decir que x se acercará a 0 a través de valores negativos.
Para observar el fenómeno usamos la misma tabla anterior, solo que cambiamos los signos de x, lo cual trae como consecuencia que los signos de 1/x también cambien; he aquí la tabla:
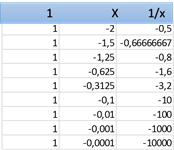
En este cuadro se observa que a medida que x se aproxima a 0 a través de valores negativos, 1/x decrece infinitamente.
Ahora bien, vamos a formalizar algunos conceptos.
Función Recíproca
La forma algebraica para definir la función recíproca es f(x)= 1/x, la cual se encuentra definida para todo número real x diferente de 0. Esto significa que su dominio se encuentra definido en R* (números reales diferentes de 0)
Estudiemos su gráfica:
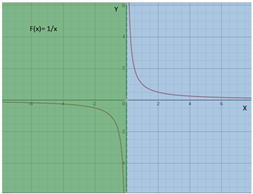
Nota: La gráfica fue generada por la calculadora gráfica Desmos. https://www.desmos.com/calculator?lang=es
Notemos que la gráfica está dividida en dos colores, verde y azul; el verde ocupa el área de la gráfica donde x<0, en este caso si nos orientamos en el sentido de izquierda a derecha acercándonos a 0 por su lado izquierdo, notaremos que la curva que define a la función se va acercando al semieje negativo Y, en el tercer cuadrante; al hacerse x cada vez más cercano a 0, la curva se hace más próxima al semieje negativo de Y, pero sin tocarlo, en este caso decimos que la curva es asintótica al eje Y.
Toda esta interpretación tiene una formalización verbal:
En este caso diremos que la Función Recíproca f(x)= 1/x decrece indefinidamente cuando x se aproxima a 0 a través de valores negativos, lo cual queda expresado simbólicamente así:
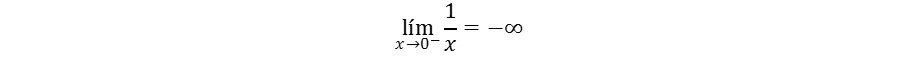
Similarmente, el lado azul de la gráfica corresponde a x>0, y haciendo un razonamiento similar al anterior se puede deducir que a medida que x se aproxima a 0 a través de valores positivos, f(x)= 1/x crece indefinidamente, en este caso diremos que el Límite de 1/x cuando x tiende a 0 por la derecha es + ∞.
Y escribimos:
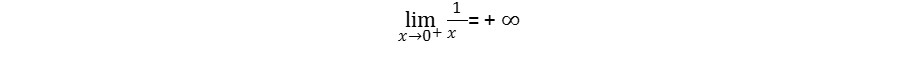
En este casos decimos que la recta x=0 es una asíntota vertical.
A continuacion un ejercicio donde podamos aplicar esta generalización.
Estudiemos el caso de f(x)= 1/(x-2)
El dominio de esta función es R-{2}, es decir todos los números reales a excepción de 2.
Veamos qué pasa con la función cuando x se aproxima a 2 tanto por la izquierda como por la derecha:

Para calcular estos límites nos valemos de la siguiente estrategia: tomamos un valor muy próximo a 2 tanto por la izquierda como por la derecha por ejemplo: por la izquierda podemos considerar x=1,9; y por la derecha x=2,1. Sustituimos estos valores en los límites 1 y 2, obteniendo lo siguiente:

La gráfica de esta función corresponde a la misma gráfica de la función reciproca trasladada dos unidades a la derecha, siendo la asíntota vertical la recta x=2.
Dejo la elaboración de la gráfica al lector.
Nota
Creé la imagen inicial la con la ayuda de Paint, los cuadros con excel y la gráfica matemática con la Calculadora Gráfica Desmos.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Thank you very much for your recognition.
Dear @analealsuarez, we need your help!
The Hivebuzz proposal already got an important support from the community. However, it lost its funding few days ago and only needs a few more HP to get funded again.
May we ask you to support it so our team can continue its work this year?
You can do it on Peakd, ecency,
https://peakd.com/me/proposals/199
Your support would be really helpful and you could make the difference! Thank you!