Recordemos que la función constante se define como función polinomica de grado 0, esto es: f(x)= ax0 donde a, es una constante (cualquier número real) y x0=1; esto significa que nuestra función queda simplificada a la siguiente forma:
f(x)=a, siendo su dominio .gif)
el conjunto de los números reales.
Es importante destacar que la gráfica de la función constante es una recta horizontal
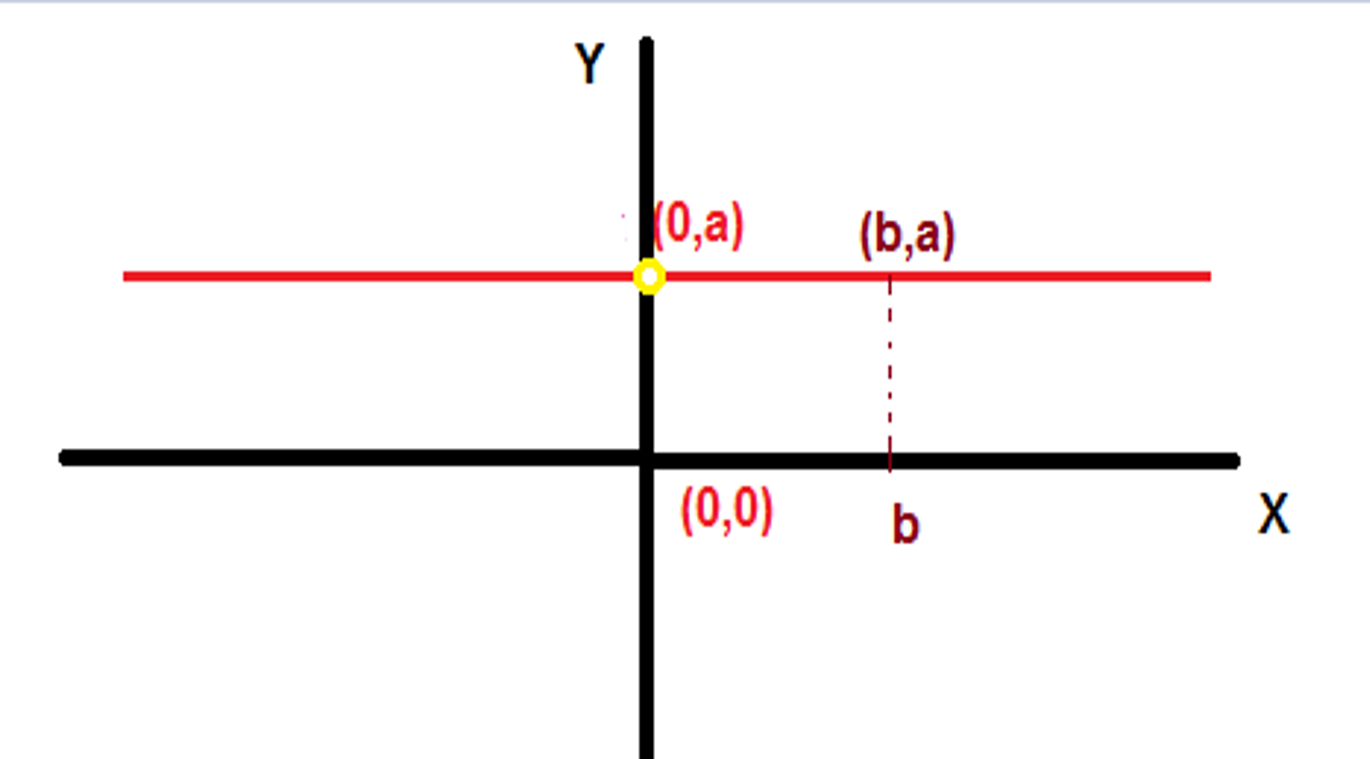
Debemos recordar que y=f(x), de acuerdo a la notación funcional.
Consecuentemente en este caso la recta tangente también es horizontal, de manera que su pendiente es 0 (toda recta horizontal tiene pendiente 0).
Recordemos (ver mi post anterior) que la derivada de una función en un punto dado viene siendo la pendiente de la recta tangente al gráfico de esa función en ese punto.
Esto es:
.gif)
Se deduce de acuerdo a lo anterior que la derivada de la función contante es 0 en cualquier punto.
Vamos a demostrarlo:
.gif)
De acuerdo a la definición de nuestra función f(x)=a, para todo x en su dominio, se concluye que:
.gif)
Y de igual manera:
.gif)
Por lo cual:
.gif)
De esta manera validamos lo que se dijo al comienzo y afirmamos que, en general, la derivada de una función constante es 0.
Veamos algunos ejemplos
Si:
f(x)= 1 entonces f´(x)=0
g(x)= 2/3 entonces g´(x)=0
h(x)=0, entonces h´(x)=0
▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄
Créditos
Usamos el Editor de Ecuaciones latex para editar las ecuaciones.
Paint para las gráficas
PawerPoint para editar las gráficas
El contenido es totalmente original.
Su post ha sido valorado por @ramonycajal
Congratulations your publication has been chosen among the best of the day.
KEEP CREATING GOOD CONTENT.