Comment envoyer une transaction Bitcoin à la main ?

Je me suis récemment mis en tête d'envoyer une transaction « à la main » pour me familiariser avec le protocole Bitcoin. Plutôt que d'utiliser un portefeuille logiciel qui cache tout le processus mis en place, je voulais écrire un programme minimaliste qui puisse créer et envoyer une transaction simple sur le réseau. La tâche s'est avérée plus difficile que prévue, car Bitcoin est plus complexe que ce que l'on s'imagine et permet de faire bien plus de choses que de simples paiements.

Les transactions contituent l'élément central de Bitcoin : le protocole est conçu pour qu'elles puissent être créées, propagées sur le réseau, validées et ajoutées à la chaîne de blocs. Ce n'est pas un hasard car ce qui donne de la valeur au bitcoin, c'est la possibilité de pouvoir le transférer le plus facilement possible. Sans transaction, Bitcoin n'existe plus car toutes les incitations qui le font fonctionner s'effondrent.

Cet article concerne les transactions sur le réseau Bitcoin Cash (BCH), ainsi que les transactions « classiques » sur le réseau Bitcoin (BTC). Par transactions classiques, j'entends les transactions originelles qui étaient les seules avant l'activation de SegWit le 24 août 2017. SegWit (abbréviation de Segregated Witness) est une évolution rétrocompatible du protocole Bitcoin (soft fork) qui modifie en profondeur la structure des transactions. Présenter les changements relatifs à cette mise à jour mériterait un article entier : d'où mon choix de ne présenter ici que les transactions classiques, qui restent heureusement valides sur le réseau BTC.

Ma description est volontairement très détaillée et s'adresse aux développeurs (et aux curieux) souhaitant comprendre Bitcoin plus en profondeur. Je vais d'abord décrire comment fonctionnent les transactions, avant d'expliquer ensuite comment en construire une et enfin de la propager sur le réseau.¹

Comment fonctionnent les transactions ?

On se fait intuitivement une vision assez simple des transactions Bitcoin. Une transaction peut être caractérisée à l'aide des informations suivantes :

Une adresse (« un compte ») d'envoi dont le solde en bitcoins est inférieur au montant à envoyer ;
Une adresse de réception ;
Un montant à envoyer ;
Des frais à payer au réseau.

De plus, pour qu'elle soit acceptée par le réseau, la transaction a besoin d'être signée électroniquement par la clé privée (« le mot de passe ») liée à l'adresse d'envoi.

Par exemple, disons qu'Alice, heureuse propriétaire de 16 milli-bitcoins (1 milli-bitcoin = 0.001 bitcoin), veuille envoyer 12 milli-bitcoins à Bob. Pour cela, elle n'a qu'à dire au réseau « Moi, Alice, envoie 12 milli-bitcoins à Bob. » en signant électroniquement cette déclaration à l'aide de sa clé privée. Les validateurs du réseau (les mineurs) vérifient bien qu'Alice détient bien assez de bitcoins et vérifient sa signature. Si tout est en ordre, ils inscrivent la transaction sur la chaîne de blocs, registre contenant toutes les transactions ayant jamais eu lieu. Après l'opération, Alice se retrouve avec 4 milli-bitcoins en sa possession, et Bob en possède 12.

Cependant, ce n'est que la surface du processus et la réalité est un petit peu plus complexe que cela comme nous allons le voir dans la suite.

Clé privée, clé publique et adresse

Pour comprendre les transactions, il est nécessaire savoir ce qu'est une clé privée, une clé publique et une adresse, et comment elles sont liées mathématiquement.

Comme je l'explique dans un article précédent, la clé privée est un nombre aléatoire compris entre 1 et 2²⁵⁶ (qui vaut environ 1.1579 × 10⁷⁷) : en générer une revient donc à choisir un nombre au hasard dans cet intervalle. Cette clé privée est une information censée rester secrète.

La clé publique est calculée à partir de la clé privée à l'aide de l'algorithme ECDSA (Elliptic Curve Digital Signature Algorithm), qui est aussi l'algorithme de signature des transactions. Cette opération est à sens unique : retrouver la clé privée à l'aide de la clé publique est virtuellement impossible, et c'est pour cela que la clé publique peut être divulguée sans risque.

Sauf cas exceptionnel (adresse multisignature par exemple), l'adresse Bitcoin est obtenue à partir de la clé publique : elle est le résultat du passage de la clé publique par les fonctions de hachage SHA256 et RIPEMD160. Ces fonctions sont également à sens unique et leur composée se note communément HASH160. Ainsi, chaque adresse de ce type (noté P2PKH pour Pay-to-Pubkey-Hash) est liée à une clé privée. De ce fait, seule la clé privée permet de dépenser les bitcoins présents à l'adresse qui lui correspond, car elle seule peut signer électroniquement une transaction provenant de cette adresse.

Pour être enregistrées et partagées, les clés privées et les adresses sont encodées en base 58 sous la forme de chaînes de caractères alphanumériques. Plus précisément, Bitcoin utilise l’encodage Base58Check qui ajoute une somme de contrôle (checksum) à la fin du nombre en lui-même pour permettre aux logiciels de détecter les erreurs de copie (typiquement une faute de frappe dans une adresse). Sur le réseau Bitcoin Cash, l'encodage en Base58Check pour les adresses est valide mais il arrive souvent que les adresses soient encodées dans un autre format appelé CashAddr qui est correspond à une représentation en base 32.

Sorties transactionnelles

Comme je l'ai dit les transactions représentent l'élément central de Bitcoin, à tel point que tout est construit autour d'elles. En effet, Bitcoin repose sur les sorties transactionnelles (transaction outputs), qui constituent les briques élémentaires du système. En fait, les bitcoins n'existent qu'en tant que sorties transactionnelles : un montant de bitcoins existe à une adresse, non pas parce que cette adresse est enregistrée dans la chaîne de blocs comme possédant ce montant, mais parce que ce montant est le résultat d'une transaction confirmée vers cette adresse. Même les bitcoins nouvellement créés par le minage sont des sorties transactionnelles : ils proviennent d'une transaction spéciale appelée coinbase qui est présente au début de chaque bloc miné.

En particulier, les bitcoins dépensables sont liés à ce qu'on appelle les sorties transactionnelles non dépensées ou UTXO (de l'anglais Unspent Transaction Output). Tout comme la chaîne de blocs, l'ensemble des UTXO (UTXO set) est conservé par tous les nœuds complets du réseau. Ceci permet de vérifier rapidement si tel ou tel montant de bitcoin est dépensable ou non.

La façon dont sont construites les transactions est fondée sur la gestion de ces UTXO. Une transaction consiste a déverrouiller un ou plusieurs UTXO (appelées alors entrées) et à verrouiller le montant total dans un ou plusieurs UTXO (appelées alors sorties). Un UTXO, de par sa nature de sortie transactionnelle, ne peut pas être partiellement dépensé : c'est pourquoi les portefeuilles renvoient normalement un certain montant vers l'une des adresses de l'utilisateur quand tous les bitcoins en sa possession ne sont pas dépensés (c'est ce qu'on appelle « rendre la monnaie »). Le schéma ci-dessous présente une transaction se déroulant entre deux personnes, Alice et Bob.

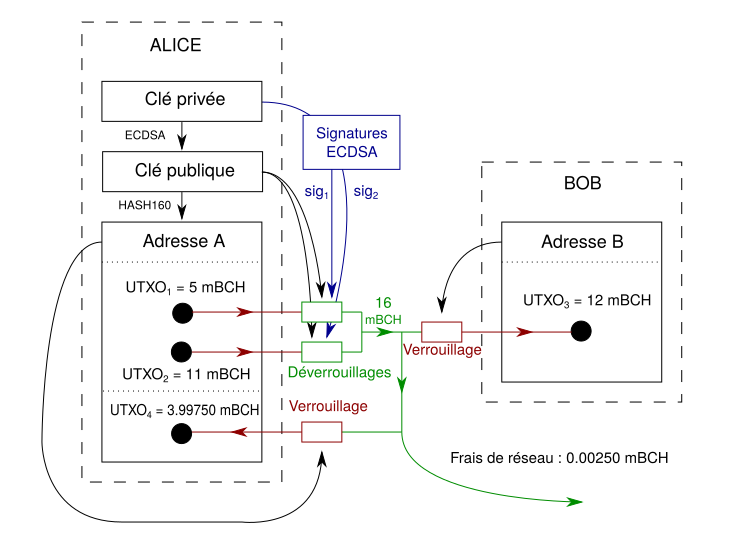
Dans cet exemple, Alice (adresse A) possède 16 milli-bitcoins et veut envoyer 12 milli-bitcoins à Bob (adresse B). Alice a précédemment reçu 2 paiements à son adresse : un de 5 milli-bitcoins et un de 11 milli-bitcoins. Puisque le montant à envoyer est de 12 milli-bitcoins, elle doit nécessairement utiliser les deux UTXO liés à ces paiements. Pour réaliser la transaction, elle procède de la manière suivante :

Elle déverrouille les deux UTXO précédents (1 et 2) en signant avec sa clé privée et en fournissant sa clé publique pour que les autres acteurs du réseau puissent vérifier sa signature.
Elle verrouille un UTXO (3) de 12 milli-bitcoins à l'adresse de Bob, qui sera le seul à pouvoir déverrouiller.
Elle se « rend la monnaie » en verrouillant un UTXO (4) de 3.99750 milli-bitcoins à sa propre adresse.
Le reste (le montant total des 2 entrées moins le montant total des 2 sorties) est payé comme frais de réseau aux mineurs : ici 0.00250 milli-bitcoins.

Des explorateurs de blocs permettent d'observer les transactions présentes sur la chaîne de blocs. On peut citer blockdozer.com pour BCH et blockchain.info pour BTC. Les transactions sont usuellement connues sur le réseau grâce à leur identifiant, qui est une chaîne de 64 caractères hexadécimaux (comme par exemple 78e9f36ba381c4cd7f2219d87bb1555134b9c9a4bfb44ae74ebb499244b9ef6a). Pour retrouver une transaction, on peut taper son identifiant dans la barre de recherche de l'explorateur. Ou bien on peut rechercher l'une des adresses impliquées dans la transaction et retrouver celle-ci dans l'historique de cette adresse.

Construire une transaction

La construction d'une transaction est basée sur ce concept d'UTXO. Chaque UTXO est caractérisé par l'identifiant de la transaction dont il est issu, ainsi que sa position dans cette transaction (index). Chaque UTXO possède également une valeur. Cependant, il faut savoir que la valeur d'un UTXO ne s'exprime pas en bitcoins, mais en satoshis. Le satoshi est la plus petite unité de mesure du système et vaut un cent-millionième de bitcoin (0.00000001 bitcoin). Il est nommé ainsi en hommage au créateur de Bitcoin, Satoshi Nakamoto.

Je prendrai l'exemple d'une transaction Bitcoin Cash tout au long de cet exposé, mais je préciserai si les choses se passent autrement sur le réseau BTC. En fait, j'ai envoyé la même transaction sur les deux réseaux, mais certains détails diffèrent inévitablement.

Ma transaction se veut minimale. Elle s'effectue entre deux adresses simples (c'est-à-dire de type P2PKH). L'ensemble du montant présent à la première adresse est entièrement dépensé. Les détails relatifs à ma transaction sont :

L'adresse d'envoi : 1LYiZn2J36VJ2nSnfpBEvKqktYPt7A2ckz (qui est aussi représentée sur le réseau BCH par qrtxn76ytspdnsj8hg5v4sny2mqv0favku8x6xqp5x).
La clé privée correspondant à cette adresse pour pouvoir signer la transaction : 5KZKPFt7ai4ytTpsR5ZBz5C9aALSYY715TXBcvzoDd9sKnPfcCf. Il va sans dire que, la clé privée étant révélée ici, tout montant envoyé à l'adresse ci-dessus sera sans doute dépensé immédiatement.
L'adresse de réception : 1GpSjtgw6fqfiZ6U5xxjbcUr4TWeCrrYj9 (qui est aussi représentée sur le réseau BCH par qzkc9mzhuruhvg4dmyh5ty2dwkx2vnn4u5kw7r64ad).
Les frais à payer pour la transaction. Ceux-ci sont proportionnels à la taille de la transaction. Leur taux est fixe pour le réseau BCH : 1 satoshi par octet. Cependant, les frais sur le réseau BTC doivent être calculés dynamiquement : comme les blocs sont régulièrement pleins, les frais dépendent de ce que les autres sont prêts à payer ; ce qui, en cas de forte demande, est susceptible d'exploser. Pour savoir quels frais payer, on peut se reporter au site bitcoinfees.earn.com qui donne en direct les informations nécessaires. Par chance, au moment où j'ai réalisé la transaction, les frais étaient au plus bas. La taille d'une transaction étant généralement de 225 octets, j'ai payé 250 satoshis de frais pour être un peu au-dessus de l'actuel taux minimal standard fixé à 1 sat/o. Cela représentait au moment de la transaction 0.002 € pour BCH et 0.017 € pour BTC.
Le montant à envoyer. J'ai envoyé le montant maximal à l'adresse de réception. J'avais 41 424 satoshis à dépenser auxquels j'ai soustrait les 250 satoshis de frais : ce qui me donnait 41 174 satoshis à envoyer.

Pour construire ma transaction, j'avais également besoin de connaître les informations concernant l'UTXO précédent :

L'identifiant de la transaction dont il est issu : 0b6e3e3506df02cd5726c924f427cdfca302293107d66dd54d739bba9ae47030 sur le réseau BCH et be1bfe88f844ba76f978306ec5a9fbf2ef0df9e42030e2067fb13b9d31b2f85c sur le réseau BTC.
Son index c'est-à-dire sa position dans cette transaction : ici 0 puisqu'il occupe la première position.
Sa valeur : 41 424 satoshis.

Structure générale de la transaction

Les données sont transmises sur le réseau sous la forme de flux d'octets. L'octet (appelé byte en anglais) est un ensemble de 8 bits d'information. Si les bits sont usuellement représentés par le système binaire (un bit vaut 0 ou 1), les octets sont quant à eux codés à l'aide du système hexadécimal (base 16). Celui-ci est en effet plus commode pour représenter les octets : un octet est symbolisé par 2 caractères au lieu de 8 dans le système binaire. Pour indiquer qu'on utilise le système hexadécimal, le préfixe 0x est souvent placé avant le nombre en question (0x9e par exemple, qui est égal à 10011011 en binaire et 158 en base 10).

Les flux d'octets peuvent être donnés dans le sens ordinaire (big-endian) ou dans le sens inverse (little-endian). Assez étrangement, Bitcoin utilise alternativement les deux conventions pour écrire les informations. Je préciserai dans chaque cas quel est l'ordre des octets.

Ma transaction se présente sous la forme brute suivante (j'ai volontairement mis des espaces entre chaque octet) :

01 00 00 00 01 30 70 e4 9a ba 9b 73 4d d5 6d d6 07 31 29 02 a3 fc cd 27 f4 24 c9 26 57 cd 02 df 06 35 3e 6e 0b 00 00 00 00 8a 47 30 44 02 20 0a a9 9d 80 c7 59 e5 ec 75 88 87 da 64 90 f0 60 17 47 67 51 62 80 06 f2 ab 5d 58 00 7b 97 89 9a 02 20 72 70 5d fe 33 1c d1 7a 82 0f 20 cc 51 89 b4 9f 72 11 84 1e 4b 3b 81 24 a1 ab 12 5d 84 84 9e 53 41 41 04 de d4 d6 4f 36 b6 6f 55 f4 c8 f5 3f e4 18 3c a4 fb 61 d3 c8 55 03 43 47 90 43 a4 89 68 73 a1 8a 77 69 4c c1 5f 47 5f 94 fe c6 39 65 0f fe 1c cf 0c 96 e9 4b 3f 92 fb ab 4b 50 ad 81 0d 17 78 15 fe ff ff ff 01 d6 a0 00 00 00 00 00 00 19 76 a9 14 ad 82 ec 57 e0 f9 76 22 ad d9 2f 45 91 4d 75 8c a6 4e 75 e5 88 ac 63 09 08 00

Dans la suite, je présenterai les détails de cette transaction dans des tableaux. Dans ces tableaux, on décrira chaque donnée tout en donnant son nom anglais, sa taille en octets, l'ordre dans lequel sont écrits les octets, et sa valeur en hexadécimal.

Une transaction se divise en quatre partiess :

Le numéro de version (version) ;
Les entrées (inputs) ;
Les sorties (outputs) ;
Le temps de verrouillage (locktime).

Ici, j'ai construit une transaction à une seule entrée et à une seule sortie, ce qui me simplifiait la tâche. Ma transaction était structurée de la façon suivante :

Nom	Taille	Ordre	Description	Valeur
version	4	Inverse	Numéro de version de la transaction. Ici égal à 1. Il existe des transactions de version 2.	01 00 00 00
input count	1	Ordinaire	Nombre d'entrées de la transaction. Ici une seule.	01
previous output txid	32	Inverse	Identifiant de la transaction dont est issu l'UTXO à dépenser.	30 70 e4 9a ba 9b 73 4d d5 6d d6 07 31 29 02 a3 fc cd 27 f4 24 c9 26 57 cd 02 df 06 35 3e 6e 0b
previous output index	4	Inverse	Position de l'UTXO à dépenser dans la transaction ci-dessus. La première position est 0.	00 00 00 00
size	1	Ordinaire	Taille du script de déverrouillage.	8a
unlocking script	138	Ordinaire	Script de déverrouillage aussi appelé scriptSig.	Voir plus bas.
sequence	4	Inverse	Numéro de séquence. Fixé à `0xffffffff - 1` pour autoriser le locktime.	fe ff ff ff
output count	1	Ordinaire	Nombre de sorties de la transaction. Ici une seule.	01
amount	8	Inverse	Montant envoyé en satoshis. Ici 41174 (`0xa0d6`).	d6 a0 00 00 00 00 00 00
size	1	Ordinaire	Taille du script de verrouillage.	19
locking script	19	Ordinaire	Script de verrouillage aussi appelé scriptPubkey.	Voir plus bas.
locktime	4	Inverse	Temps de verrouillage. Si strictement supérieur à 0 et inférieur à 500 millions : interprété comme hauteur de bloc ; si strictement supérieur à 500 millions : interprété comme horodatage de l'Ère Unix (nombre de secondes depuis le 1/1/1970 00:00 UTC). Ici la hauteur du dernier bloc miné : 526691 (`0x080963`).	63 09 08 00

Construction des scripts

Comme on l'a vu, une transaction consiste à déverrouiller un ou plusieurs UTXO en entrée pour en verrouiller un ou plusieurs en sortie. Pour ce faire, Bitcoin utilise des scripts spécifiques. Cela a été conçu de la sorte pour donner aux transactions un caractère programmable et pour permettre un large éventail d'actions.

Le langage de programmation de Bitcoin (appelé de façon peu originale Script) est un langage qui se base sur une pile (stack), tout comme les langages informatiques des années 1960. Ce langage se compose d'une centaine de codes opératoires (ou OP codes). Il permet entre autres de créer des adresses multisignatures, d'inscrire des données brutes sur la chaîne de bloc (OP_RETURN) ou de construire des « jetons colorés », c'est-à-dire des bitcoins spéciaux ayant des caractéristiques supplémentaires.

Ici nous avons deux scripts. Regardons de quoi ils sont constitués avant de voir comment ils sont exécutés. Le script de déverrouillage (historiquement appelé scriptSig) est composé de la signature et de la clé publique de celui qui signe la transaction. Il permet de déverrouiller l'UTXO précédent présent à l'adresse d'envoi. Il s'écrit sous la forme :

Nom	Description	Valeur
PUSHDATA 71	Pousse 71 (`0x47`) octets sur la pile.	47
signature	Signature sous forme sérialisée (DER) et type de signature.	30 44 02 20 0a a9 9d 80 c7 59 e5 ec 75 88 87 da 64 90 f0 60 17 47 67 51 62 80 06 f2 ab 5d 58 00 7b 97 89 9a 02 20 72 70 5d fe 33 1c d1 7a 82 0f 20 cc 51 89 b4 9f 72 11 84 1e 4b 3b 81 24 a1 ab 12 5d 84 84 9e 53 41
PUSHDATA 65	Pousse 65 (`0x41`) octets sur la pile.	41
pubkey	Clé publique sous forme sérialisée.	04 de d4 d6 4f 36 b6 6f 55 f4 c8 f5 3f e4 18 3c a4 fb 61 d3 c8 55 03 43 47 90 43 a4 89 68 73 a1 8a 77 69 4c c1 5f 47 5f 94 fe c6 39 65 0f fe 1c cf 0c 96 e9 4b 3f 92 fb ab 4b 50 ad 81 0d 17 78 15

Le script de verrouillage quant à lui permet de verrouiller l'UTXO suivant à l'adresse du récepteur de la transaction. Il est historiquement appelé scriptPubKey en référence aux adresses simples (P2PKH) dérivées directement de la clé publique. Il s'écrit sous la forme :

Nom	Description	Valeur
OP_DUP	Duplique l'objet en haut de la pile.	76
OP_HASH160	Calcule le hachage de l'objet par la composée des fonctions SHA256 et RIPEMD160.	a9
PUSHDATA 20	Pousse 20 (`0x14`) octets sur la pile.	14
address	Charge utile de l'adresse (public key hash).	ad 82 ec 57 e0 f9 76 22 ad d9 2f 45 91 4d 75 8c a6 4e 75 e5
OP_EQUALVERIFY	Rend la transaction invalide si les deux objets en haut de la pile ne dont pas égaux.	88
OP_CHECKSIG	Vérifie que la clé publique présente en haut de la pile correspond bien à la signature en dessous.	ac

Comment ces scripts fonctionnent-ils ? Considérons un exemple : prenons notre script de déverrouillage, et combinons-le avec le script de verrouillage du précédent UTXO, c'est-à-dire celui qui a été exécuté dans la transaction précédente et qui est lié à notre adresse. On obtient le script suivant :

47 signature 41 pubkey OP_DUP OP_HASH160 14 address OP_EQUALVERIFY OP_CHECKSIG

Comme précisé plus haut, ce script agit sur une pile au sommet de laquelle sont poussées les données (signature, clé publique, adresse). Ainsi, il est exécuté de la manière suivante :

Pile	Description du script
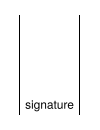	47 signature La signature (`0x47` = 71 octets) est poussée sur le haut de la pile.
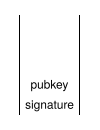	41 pubkey La clé publique (`0x41` = 65 octets) est poussée sur le haut de la pile.
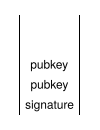	OP_DUP La clé publique est dupliquée.
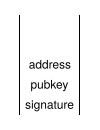	OP_HASH160 On calcule le HASH160 de la clé publique en haut de la pile, ce qui la transforme en adresse.
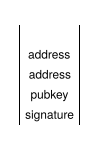	14 address L'adresse (`0x14` = 20 octets) est poussée sur le haut de la pile.
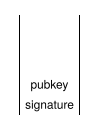	OP_EQUALVERIFY Les deux adresses sont comparées : si elles ne sont pas identiques le script est invalide ; si elles sont égales elles sont supprimées et le script poursuit son exécution.
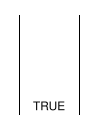	OP_CHECKSIG On vérifie que la signature correspond bien à la clé publique. Si c'est le cas, la valeur TRUE est poussée sur le haut de pile et le script est considéré comme valide.

Signature de la transaction

Le dernier élément dont j'avais besoin pour la construction de ma transaction était la signature. Puisque tous les UTXO en entrée doivent être déverrouillés, il est nécessaire de produire une signature pour chaque entrée de la transaction. Dans mon cas, je n'avais qu'une entrée : il n'y avait donc qu'une signature à créer.

Chaque signature possède un type (Signature Hash Type). Le type de la signature détermine quelles parties de la transaction elle doit signer. Le type par défaut, noté SIGHASH_ALL, signe toutes les entrées et toutes les sorties. Il est égal à 0x01 pour BTC et à 0x41 pour BCH. C'est celui que j'ai utilisé ici.

Pour pouvoir produire la signature, il faut construire en premier lieu ce qu'on appelle une préimage. Historiquement, il s'agit d'une transaction temporaire ayant la même structure qu'une transaction classique, à ceci près qu'il faut :

Remplacer les scripts de déverrouillage (scriptSig) par les scripts de verrouillage (scriptPubKey) des UTXO précédents correspondants ;
Rajouter à la transaction le type de signature (Signature Hash Type) codé sur 4 octets (en ordre inverse).

Cette préimage est utilisée pour les transactions classiques sur le réseau BTC.

Pour les transactions du réseau BCH, on contruit la préimage en suivant le standard défini par le BIP-143 décrit dans le tableau ci-dessous :

Nom	Taille	Ordre	Description	Valeur
version	4	Inverse	Numéro de version de la transaction. Ici égal à 1.	01 00 00 00
hash previous outputs	32	Ordinaire	Double SHA256 de la sérialisation des identifiants de transaction et des index de toutes les entrées de la transaction. Ici le double SHA256 de l'identifiant et de l'index de l'UTXO à dépenser.	c5 bc 71 18 d1 be a8 d9 46 0f 9a a0 d5 f6 10 83 d7 6f 75 6a 98 0e fa 91 69 ee 1d c8 20 2d 5f c3
hash sequences	32	Ordinaire	Double SHA256 de la sérialisation des numéros de séquence de toutes les entrées de la transaction. Ici le double SHA256 du numéro de séquence.	18 60 6b 35 0c d8 bf 56 52 66 bc 35 2f 0c ad dc f0 1e 8f a7 89 dd 8a 15 38 63 27 cf 8c ab e1 98
previous output txid	32	Inverse	Identifiant de la transaction de laquelle est issu l'UTXO à dépenser.	30 70 e4 9a ba 9b 73 4d d5 6d d6 07 31 29 02 a3 fc cd 27 f4 24 c9 26 57 cd 02 df 06 35 3e 6e 0b
previous output index	4	Inverse	Position de l'UTXO à dépenser dans la transaction ci-dessus. La première position est 0.	00 00 00 00
size		Ordinaire	Taille du script de verrouillage de UTXO à dépenser.	19
previous locking script	25	Ordinaire	Script de verrouillage de l'UTXO à dépenser.	76 a9 14 d6 69 fb 44 5c 02 d9 c2 47 ba 28 ca c2 64 56 c0 c7 a7 ac b7 88 ac
previous output value	8	Inverse	Valeur de l'UTXO à dépenser.	d0 a1 00 00 00 00 00 00
sequence	4	Inverse	Numéro de séquence. Fixé à `0xffffffff - 1` pour autoriser le locktime.	fe ff ff ff
hash outputs	32	Ordinaire	Double SHA256 de la sérialisation des montants et des scripts de verrouillage (tailles incluses) de toutes les sorties de la transaction. Ici on n'a qu'une seule sortie.	81 76 61 01 b8 4e 2d f2 50 88 2b da b0 0d e6 c8 08 39 26 77 44 42 77 9e 79 a6 c1 4c 21 2d 01 ae
locktime	4	Inverse	Temps de verrouillage.	63 09 08 00
hashtype	4	Inverse	Type de signature.	41 00 00 00

Une fois la préimage construite, on peut calculer la signature. Il s'agit de signer le double SHA256 de la préimage avec la clé privée à l'aide de l'algorithme ECDSA. La signature résultante est composée de deux nombres : R et S. Pour des raisons de sécurité², les nœuds du réseau ne relaient que les signatures à petite valeur de S. La signature est sérialisée selon le standard d'encodage international appelé Distinguished Encoding Rules (DER). À celle-ci, il faut ajouter le type de signature encodé sur 1 octet. Dans notre cas on obtient :

Nom	Description	Valeur
sequence	Indique le début d'une séquence DER.	30
size	Taille de la séquence	44
integer	Annonce un entier.	02
size	Taille de l'entier R.	20
R		0a a9 9d 80 c7 59 e5 ec 75 88 87 da 64 90 f0 60 17 47 67 51 62 80 06 f2 ab 5d 58 00 7b 97 89 9a
integer	Annonce un entier.	02
size	Taille de l'entier S.	20
S		72 70 5d fe 33 1c d1 7a 82 0f 20 cc 51 89 b4 9f 72 11 84 1e 4b 3b 81 24 a1 ab 12 5d 84 84 9e 53
hashtype	Type de signature.	41

Identifiant de la transaction

Enfin il me restait à calculer l'identifiant de ma transaction pour pouvoir la retrouver sur la chaîne de blocs. L'identifiant d'une transaction est obtenu en calculant le double SHA256 de la transaction brute (forme hexadécimale) puis en inversant l'ordre des octets. Pour ma transaction Bitcoin Cash, j'ai obtenu :

b259e3b577af3ed68fac38e71e39bcfee6ad2080cbee753394690afa2a5dc69d

Communiquer avec le réseau pour envoyer une transaction

Il était possible de passer par un tiers pour diffuser ma transaction (blockdozer.com pour BCH, blockchain.info pour BTC). Cependant je tenais à me connecter directement au réseau et communiquer avec lui pour la propager de la façon la plus authentique possible.

Connexion au réseau

Le réseau Bitcoin est un réseau pair-à-pair appartenant au réseau Internet et utilisant donc les protocoles TCP/IP pour fonctionner. Les membres du réseau sont appelés des nœuds. Les nœuds sont identifiés par leur adresse IP (IP pour Internet Protocol). Bitcoin utilise pour cela les adresses IPv6 (adresses de version 6). Pour les nœuds possédant des adresses IPv4 (adresses de version 4 tout récemment épuisées), il est nécessaire de les écrire comme des adresses IPv6 : par exemple, l'adresse IPv4 127.0.0.1 devient 00000000000000000000ffff7f000001 en IPv6. Le numéro de port est lui laissé par défaut à 8333.

Pour trouver un nœud auquel me connecter, je me suis servi d'une liste en ligne des nœuds actifs du réseau, donnant leur adresse IP et leur numéro de port. Il s'agissait de CashNodes pour BCH et Bitnodes pour BTC.

Pour me connecter à un nœud et lui envoyer des messages, j'ai utilisé le paquet socket de Python. La connexion se faisait de la manière suivante :

import socket
sock = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
host = # [adresse ip du nœud]
port = # [numéro de port du nœud]
sock.connect((host,port))

L'envoi et la réception de messages utilisaient les fonctions sock.send et sock.recv³.

Structure générale d'un message

Les messages envoyés sur le réseau sont structurés d'une manière précise. Tout d'abord, un message n'est pas envoyé sous forme brute ; il est précédé d'un en-tête spécifique. On présente ci-dessous comment tout message doit être structuré. On donne ici l'exemple du message de version.

Nom	Taille	Ordre	Description	Valeur (message de version)
magic	4	Inverse	Numéro magique du réseau. BTC : `0xd9b4bef9`. BCH : `0xe8f3e1e3`.	e3 e1 f3 e8
command	12	Ordinaire	Représentation ASCII du type de message suivie d'octets nuls par complétion.	76 65 72 73 69 6f 6e 00 00 00 00 00
size	4	Inverse	Taille de la charge utile : 86 (`0x56`) octets.	56 00 00 00
checksum	4	Ordinaire	Somme de contrôle : 4 premiers octets du double SHA256 de la charge utile.	3d b1 2a 3b
payload	86	Ordinaire	Charge utile : il s'agit du message en lui-même.	Voir ci-dessous.

Message de version (version)

Le message de version existe pour que nous envoyions des informations sur notre nœud (émetteur) au nœud auquel nous nous connectons (récepteur). Pour communiquer, deux nœuds doivent avoir échangé leurs messages de version. Le protocole est plutôt permissif : c'est pourquoi j'ai laissé beaucoup de paramètres par défaut. Le message de version s'organise de la manière suivante :

Nom	Taille	Ordre	Description	Valeur
version	4	Inverse	Numéro de version du protocole. Le dernier en date : 70 015 (`0x1117f`).	7f 11 01 00
services	8	Inverse	Services fournis par le nœud émetteur. Laissés par défaut à zéro.	00 00 00 00 00 00 00 00
timestamp	8	Inverse	Horodatage de l'Ère Unix (nombre de secondes depuis le 1/1/1970 00:00 UTC).	2b c7 d9 5a 00 00 00 00
addr_recv services	8	Inverse	Services fournis par le nœud récepteur.	01 00 00 00 00 00 00 00
addr_recv ip	16	Ordinaire	Adresse IPv6 du nœud récepteur vue par le nœud émetteur. Laissée par défaut à 127.0.0.1.	00 00 00 00 00 00 00 00 00 00 ff ff 7f 00 00 01
addr_recv port	2	Ordinaire	Numéro de port du nœud récepteur vu par le nœud émetteur. Laissé par défaut à 8333 (`0x208d`).	20 8d
addr_trans services	8	Inverse	Services fournis par le nœud émetteur. Doit être identique au champ services décrit plus haut.	00 00 00 00 00 00 00 00
addr_trans ip	16	Ordinaire	Adresse IPv6 du nœud émetteur. Laissée par défaut à 127.0.0.1.	00 00 00 00 00 00 00 00 00 00 ff ff 7f 00 00 01
addr_trans port	2	Ordinaire	Numéro de port du nœud émetteur. Laissé par défaut à 8333 (`0x208d`).	20 8d
nonce	8	Inverse	Nombre aléatoire généré à chaque message de version.	5b 6c 75 b4 27 13 91 ee
size	1	Ordinaire	Taille de user agent.	00
user agent	0	Inverse	Spécifie le type de logiciel utilisé pour faire fonctionner le nœud (BIP-14). Anciennement connu comme subversion.
start height	4	Inverse	Hauteur du dernier bloc miné connu par le nœud. Ici : 526691 (`0x080963`)	63 09 08 00
relay	1	Ordinaire	Égal à 1 si le nœud propage les transactions, 0 sinon.	00

Message de reconnaissance de version (verack)

En retour de mon message de version, j'ai reçu le message de version de l'autre nœud, ainsi qu'un message de reconnaissance de version (appelé verack pour version acknowledgment). Il s'agit d'un message contenant la commande verack (76 65 72 61 63 6b 00 00 00 00 00 00 00 00 00 00) et dont la charge utile est vide (sa somme de contrôle est donc toujours égale à 5d f6 e0 e2).

Message de transaction (tx)

Enfin, la dernière étape était d'envoyer mon message de transaction. Le charge utile du message correspond à la transaction brute que l'on a construite dans la partie précédente : 01 00 00 00 01 30 70 e4 ... L'en-tête de mon message était composé de :

La commande tx : 74 78 00 00 00 00 00 00 00 00 00 00.
La taille de la transaction brute, égale à 223 (0xdf) octets : df 00 00 00.
La somme de contrôle de la transaction brute : 9d c6 5d 2a.

Quand une transaction est envoyée sur le réseau, les nœuds complets qui la relaient la transfèrent dans une base de données appelée mempool qui regroupe l'ensemble des transactions non confirmées. Elle passe par trois états différents :

La transaction est d'abord vérifiée (0-conf, quelques secondes) : elle est diffusée et identifiée comme valide (fonds disponibles, pas de double-dépense, etc.) par les différents nœuds du réseau. Sur le réseau BCH, on considère que la transaction est sûre pour des petits montants dès ce stade. Sur le réseau BTC, ce n'est plus le cas.
Puis la transaction est confirmée (1-conf, 10 minutes en moyenne) : elle est inclue dans un bloc qui est validé par un mineur. Il y a encore (théoriquement) un risque de double-dépense, même si la probabilité est très, très faible.
La transaction est enfin irréversible (6-conf, 60 minutes en moyenne) : en plus du bloc contenant la transaction, 5 blocs supplémentaires sont minés. Le fait que le bloc soit enfoui dans la chaîne de blocs rend impossible toute modification : pour altérer ce bloc il faudrait d'abord modifier les 5 autres blocs. Les plateformes d'échange attendent souvent ce stade avant de laisser leurs usagers utiliser leurs fonds.

Une fois mes deux transactions envoyées, j'ai été vérifier à l'aide d'explorateurs de blocs qu'elles avaient bien été propagées et confirmées. Et en effet, c'était le cas. Ma transaction sur le réseau BCH avait été incluse dans le bloc 526 692, bloc miné le 20/04/2018 à 10:58 UTC. La transaction sur le réseau BTC, quant à elle, avait été incluse dans le bloc 519 124, bloc miné le 20/04/2018 à 14:24 UTC. Ma tâche était accomplie.

Pour conclure, je dirai que l'expérience a été très enrichissante. Me lancer ce défi m'a permis de comprendre plus en profondeur le protocole Bitcoin. Car après tout, même si l'on a étudié quelque chose théoriquement, il n'y pas de meilleur moyen d'apprendre que d'essayer de mettre en pratique la chose à laquelle on s'intéresse.

Merci d'avoir lu cet article.

Notes

1. Je me suis fortement inspiré d'un article de Ken Shirriff qui a eu la même démarche que moi.
2. Voir Enforcing Low S Values to Eliminate a Bitcoin Network Attack. Pour être plus précis, S doit être compris entre 1 et G/2, où G désigne l'ordre de la courbe elliptique secp256k1.
3. Pour plus de détails, j'ai publié le code que j'ai utilisé sur GitHub.

Crédit illustration : Pixabay (geralt)