▶️ Watch on 3Speak - Odysee - BitChute - Rumble - Telegram - YouTube - PDF Notes - Hive Notes - Summary - Sections playlist - Vector Functions playlist
In this video, I go over further into vector functions and this time do a deep dive into the arc length and curvature of a space curve. The arc length for a space curve is calculated in much the same way as for normal plane curves, by approximating the curve with polygons and taking the limit as they approach infinity, but we now have to include the z component. The curvature of a function is defined as the magnitude or length of the derivative of the unit tangent vector in terms of the arc length. The curvature describes how curved or "smooth" a space curve is. I also go over normal, binormal vectors, as well as the TNB frame, normal & osculating planes, and much more, so buckle up!
#math #vectors #calculus #arclength #curvature
Timestamps
- Intro – 0:00
- Calculus Book reference – 0:57
- Calculus book chapter – 1:17
- Topics to cover – 1:50
- Arc Length – 3:02
- Example 1: Arc Length of Circular Helix: https://www.geogebra.org/3d/gbvmtdug – 17:19
- Parameterizations and Arc Length Function – 24:55
- Example 2: Arc Length Function of a Helix – 38:05
- Curvature – 43:50
- Definition of Curvature – 49:36
- Example 3: Curvature of a Circle is 1/radius – 57:46
- Theorem: Curvature Cross Product Formula – 1:10:02
- Example 4: Curvature of a Twisted Cubic – 1:29:26
- Curvature of a Plane Curve y = f(x) – 1:39:46
- Example 5: Curvature of a Parabola: https://www.desmos.com/calculator/xfmwdwircp – 1:52:48
- The Normal and Binormal Vectors – 2:02:25
- Example 6: Unit Normal and Binormal Vectors of a Circular Helix: https://www.geogebra.org/3d/wyr5mysb – 2:09:42
- TNB Frame: Normal and Osculating Planes – 2:30:44
- Example 7: Normal and Osculating Plane of the Circular Helix – 2:33:41
- Osculating Circle – 2:52:25
- Example 8: Osculating Circle of a Parabola: https://www.desmos.com/calculator/tzb5bjsxkl – 2:53:54
- Summary of T, N, B, and κ Formulas: 3:06:08
- Outro – 3:10:28
View Video Notes Below!
Become a MES Super Fan - Donate - Subscribe via email - MES merchandise
Reuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically.
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books: "Where Did the Towers Go?" by Dr. Judy Wood
Join my forums: Hive community - Reddit - Discord
Follow along my epic video series: MES Science - MES Experiments - Anti-Gravity (MES Duality) - Free Energy - PG
NOTE 1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial- Download and read video notes.
- Read notes on the Hive blockchain $HIVE
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations: Increase video speed - Increase video audio - Text to speech (Android app) – Archive webpages
Calculus Book Reference
Note that I mainly follow along the book:
- Calculus: Early Transcendentals 7th Edition by James Stewart: Link
- I used the following solution manual for this chapter: Link
- Note: In some earlier videos I used the 6th edition.
Calculus Book Chapter
The Hive notes and sections playlist for each video of this chapter are listed below:
- Vector Functions and Space Curves - ▶️
- Derivatives and Integrals of Vector Functions - ▶️
- Arc Length and Curvature - ▶️ (THIS VIDEO)
- Motion in Space: Velocity and Acceleration
- Applied Project: Kepler's Laws
- Review
- Concept Check
- True-False Quiz
- Problems Plus
This links are also on MES Links: https://mes.fm/links
Topics to Cover
Note that the timestamps will be included in the video description for each topic listed below.
- Arc Length
- Example 1: Arc Length of Circular Helix
- Parameterizations and Arc Length Function
- Example 2: Arc Length Function of a Helix
- Curvature
- Definition of Curvature
- Example 3: Curvature of a Circle is 1/radius
- Theorem: Curvature Cross Product Formula
- Example 4: Curvature of a Twisted Cubic
- Curvature of a Plane Curve y = f(x)
- Example 5: Curvature of a Parabola
- The Normal and Binormal Vectors
- Example 6: Unit Normal and Binormal Vectors of a Circular Helix
- TNB Frame: Normal and Osculating Planes
- Example 7: Normal and Osculating Plane of the Circular Helix
- Osculating Circle
- Example 8: Osculating Circle of a Parabola
- Summary of T, N, B, and κ Formulas
Arc Length and Curvature
Arc Length
In my earlier video, we defined the length of a plane curve with parametric equations x = f(t), y = g(t), a ≤ t ≤ b, as the limit of lengths of inscribed polygons and, for the case where f' and g' are continuous, we arrived at the formula:
First recall my video on arc length of a curve on y = f(x).
Now recall my later video on arc length in parametric equations.
The length of a space curve is defined in exactly the same way (see figure below).
Suppose that the curve has the vector equation r(t) = < f(t), g(t), h(t) > , a ≤ t ≤ b, or, equivalently, the parametric equations x = f(t), y = g(t), z = h(t), where f', g', and h' are continuous.
If the curve is traversed exactly once as t increases from a to b, then it can be shown that its length is:
Notice that both of the arc length formulas above can be put into the more compact
Form:
because, for plane curves r(t) = f(t) i + g(t) j,:
and for space curves r(t) = f(t) i + g(t) j + h(t) k,
Recall the distance formula in 3D (and 2D):
Example 1: Arc Length of Circular Helix
Find the length of the arc of the circular helix with vector equation
r(t) = cos t i + sin t j + t k
from the point (1, 0, 0) to the point (1, 0, 2π).
Solution:
The arc from (1, 0, 0) to (1, 0, 2π) is described by the parameter interval 0 ≤ t ≤ 2π and so, from the compact arc length formula, we have:
Note that 2 * sqrt(2) * pi = 8.88576587631673 ≈ 8.89
The figure below shows the arc of the helix whose length is computed in Example 1.
For reference, here is the helix in the GeoGebra 3D graphing calculator:
https://www.geogebra.org/3d/gbvmtdug
Parameterizations and Arc Length Function
A single curve C can be represented by more than one vector function.
For instance, the twisted cubic:
could also be represented by the function:
where the connection between the parameters t and u is given by t = eu.
We say that the above equations are parametrizations of the curve C.
If we were to use the compact arc length equation to compute the length of C using the above two equations, we would get the same answer.
In general, it can be shown that when the compact equation is used to compute arc length, the answer is independent of the parametrization that is used.
Now we suppose that C is a curve given by a vector function
where r' is continuous and C is traversed exactly once as t increases from a to b.
We define its arc length function s by:
Thus s(t) is the length of the part of C between r(a) and r(t). (See figure below).
If we differentiate both sides of the above equation using Part 1 of the Fundamental Theorem of Calculus, we obtain:
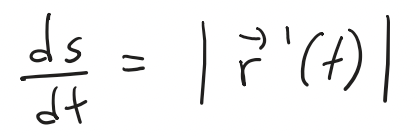
Recall my earlier videos on Part 1 and Part 2 of the Fundamental Theorem of Calculus.
It is often useful to parametrize a curve with respect to arc length because arc length arises naturally from the shape of the curve and does not depend on a particular coordinate system.
If a curve r(t) is already given in terms of a parameter t and s(t) is the arc length function given by the above equation for s(t), then we may be able to solve for t as a function of s:
t = t(s)
Then the curve can be reparametrized in terms of s for t:
r = r(t(s))
Thus, if s = 3 for instance, r(t(3)) is the position vector of the point 3 units of length along the curve from its starting point.
Example 2: Arc Length Function of a Helix
Reparametrize the helix r(t) = cos t i + sin t j + t k with respect to arc length measured from (1, 0, 0) in the direction of increasing t.
Solution:
The initial point (1, 0, 0) corresponds to the parameter value t = 0.
Recall from Example 1 the arc length of the helix:
Thus the required reparameterization is obtained by substituting for t:
Curvature
A parametrization r(t) is called smooth on an interval I if r' is continuous and r'(t) ≠ 0 on I.
A curve is called smooth if it has a smooth parametrization.
A smooth curve has no sharp corners or cusps; when the tangent vector turns, it does so continuously.
If C is a smooth curve defined by the vector function r, recall that the unit tangent vector T(t) is given by
and indicates the direction of the curve.
Recall my earlier video on unit tangent vectors.
From the figure below you can see that T(t) changes direction very slowly when C is fairly straight, but it changes direction more quickly when C bends or twists more sharply.
Unit tangent vectors at equally spaced points on C
The curvature of C at a given point is a measure of how quickly the curve changes direction at that point.
Specifically, we define it to be the magnitude of the rate of change of the unit tangent vector with respect to arc length.
We use arc length so that the curvature will be independent of the parametrization.
Definition of Curvature
The curvature of a curve is:
where T is the unit tangent vector.
Note that κ is the Greek letter Kappa, and not just a normal k.
The curvature is easier to compute if it is expressed in terms of the parameter t instead of s, so we use the Chain Rule to write:
Recall from my earlier video for the Chain Rule for vector functions.
Example 3: Curvature of a Circle is 1/radius
Show that the curvature of a circle of radius a is 1/a.
Solution:
We can take the circle to have center the origin, and then a parametrization is:
The result of Example 3 shows that small circles have large curvature and large circles have small curvature, in accordance with our intuition.
We can see directly from the definition of curvature that the curvature of a straight line is always 0 because the tangent vector is constant.
Although the curvature formula above can be used in all cases to compute the curvature, the formula given by the following theorem is often more convenient to apply.
Theorem: Curvature Cross Product Formula
The curvature of the curve given by the vector function r is:
Proof
Recall my earlier video for the Product Rule for vector functions.
Recall also from my earlier video showing that a x a = 0.
Using the fact that T x T = 0, we have:
Now |T(t)| = 1 for all t, so T and T' are orthogonal by my earlier video.
Also recall my earlier video on the length of the cross product.
Thus, by the length of the cross product theorem, we have:
Example 4: Curvature of a Twisted Cubic
Find the curvature of the twisted cubic r(t) = <t, t2, t3> at a general point and at (0, 0,0).
Solution:
We first compute the required ingredients:
At the origin, the curvature is 2.
Curvature of a Plane Curve y = f(x)
For the special case of a plane curve with equation y = f(x), we choose x as the parameter and write:
Recall my earlier video on standard basis vectors:
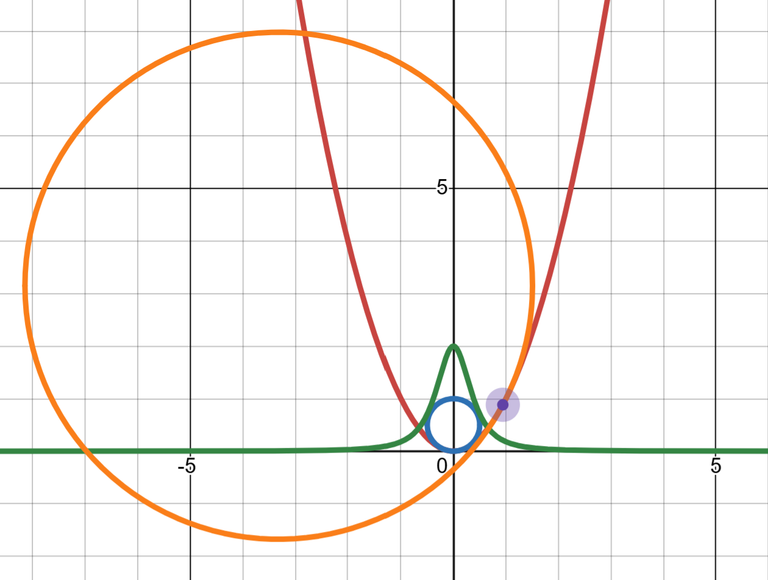
Example 5: Curvature of a Parabola
Find the curvature of the parabola y = x2 at the points (0, 0), (1, 1), and (2, 4).
Solution:
The curvature at (0, 0) is κ(0) = 2.
At (1, 1) it is κ(1) = 2/53/2 = 2/(5^(3/2)) = 0.1789 ≈ 0.18.
At (2, 4) it is κ(2) = 2/173/2 = 2/(17^(3/2)) = 0.0285 ≈ 0.03.
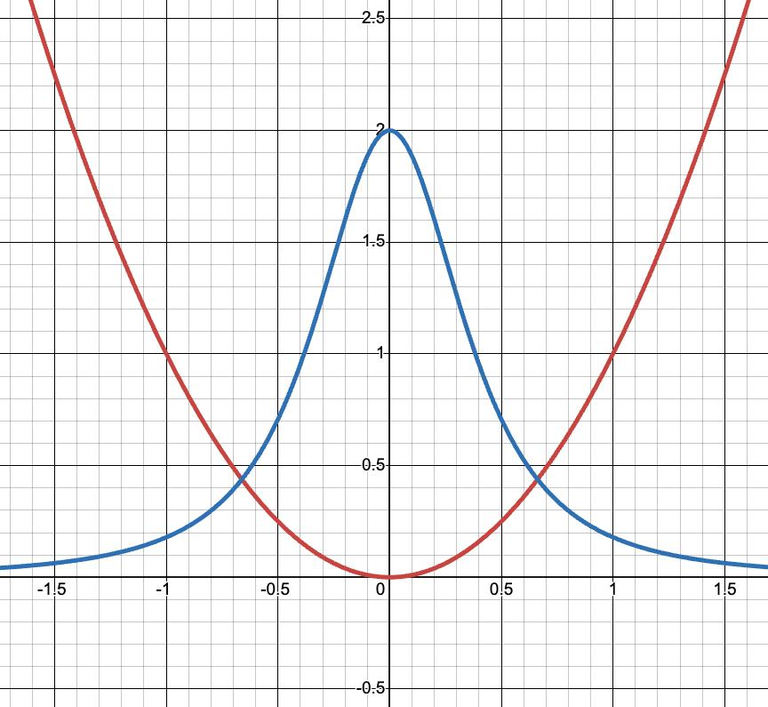
Observe from the expression for κ(x) or the graph of κ in the figure below that κ(x) → 0 as x → ± ∞.
This corresponds to the fact that the parabola appears to become flatter as x → ± ∞.
The parabola y = x2 and its curvature function.
Graphing in Desmos 2D graphing calculator, we have:
https://www.desmos.com/calculator/xfmwdwircp
The Normal and Binormal Vectors
At a given point on a smooth space curve r(t), there are many vectors that are orthogonal to the unit tangent vector T(t).
We single out one by observing that, because |T(t)| = 1 for all t, we have T(t) ⋅ T'(t) = 0 by my earlier video shown earlier, so T'(t) is orthogonal to T(t).
Note that T'(t) is itself not a unit vector.
But at any point where κ ≠ 0 we can define the principle unit normal vector N(t) (or simply unit normal) as:
The vector B(t) = T(t) x N(t) is called the binormal vector.
It is perpendicular to both T and N and is also a unit vector, see figure below.
You can think of the normal vector as indicating the direction in which the curve is turning at each point.
Example 6: Unit Normal and Binormal Vectors of a Circular Helix
Find the unit normal and binormal vectors for the circular helix:
r(t) = cos t i + sin t j + t k
Solution: We first compute the ingredients needed for the unit normal vector:
This shows that the normal vector at any point on the helix is horizontal and points toward the z-axis.
The binormal vector is:
The figure below illustrates Example 6 by showing the vectors T, N, and B at two locations on the helix.
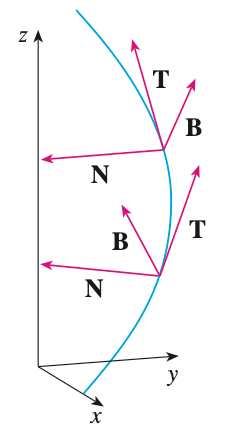
Here is a graph of the helix along with its unit tangent, unit normal, and binormal vectors in GeoGebra.
https://www.geogebra.org/3d/wyr5mysb
TNB Frame: Normal and Osculating Planes
In general, the vectors T, N, and B, starting at the various points on a curve, form a set of orthogonal vectors, called the TNB frame, that moves along the curve as t varies.
This TNB frame plays an important role in the branch of mathematics known as differential geometry and in its applications to the motion of spacecraft.
The plane determined by the normal and binormal vectors N and B at a point on a curve C is called the normal plane of C at P.
It consists of all lines that are orthogonal to the tangent vector T.
The plane determined by the vectors T and N and is called the osculating plane of C at P.
The name comes from the Latin osculum, meaning “kiss.”
It is the plane that comes closest to containing the part of the curve near P.
For a plane curve, the osculating plane is simply the plane that contains the curve.
Example 7: Normal and Osculating Plane of the Circular Helix
Find the equations of the normal plane and osculating plane of the helix in Example 6 at the point P(0, 1, π/2).
r(t) = cos t i + sin t j + t k
Solution:
The normal plane at P has normal vector r'(π/2) = <-1, 0, 1>, since:
Recall my earlier video on the equation of a plane from the normal vector:
Thus an equation of the normal plane at P is:
The osculating plane at P contains the vectors T and N, so its normal vector is T x N = B.
From Example 6 we have:
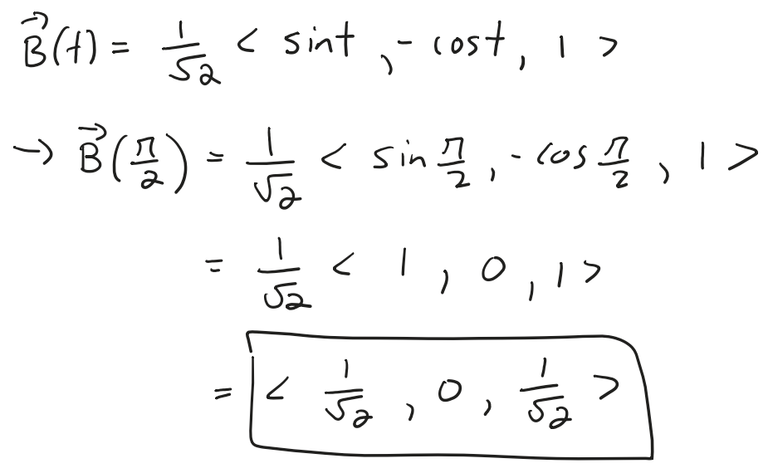
A simpler normal vector is <1, 0, 1>, so an equation of the osculating plane is:
The figure below shows the helix and osculating plane in Example 7.
For reference, here is the graph using GeoGebra:
https://www.geogebra.org/3d/wyr5mysb
Osculating Circle
The circle that lies in the osculating plane of C at P, has the same tangent as C at P, lies on the concave side of C (toward which N points), and has radius ρ = 1/κ (the reciprocal of the curvature, see Example 3) is called the osculating circle (or the circle of curvature) of C at P.
It is the circle that best describes how C behaves near P; it shares the same tangent, normal, and curvature at P.
Example 8: Osculating Circle of a Parabola
Find and graph the osculating circle of the parabola y = x2 at the origin.
Solution:
From Example 5, the curvature of the parabola at the origin is κ(0) = 2.
So, as per Example 3, the radius of the osculating circle at the origin is 1/κ = 1/2 and its center is (0, 1/2).
Its equation is therefore:
Recall from my earlier video on the equation of a circle.
For the graph in the figure below, we use parametric equations of this circle:
For reference, here is the graph using Desmos, including showing how the osculating circle changes as a point moves along the curve.
Note that I used Grok AI to obtain the general osculating circle equation.
https://www.desmos.com/calculator/tzb5bjsxkl
Summary of T, N, B, and κ Formulas
We summarize here the formulas for unit tangent, unit normal and binormal vectors, and curvature.
You can check out this post and your own profile on the map. Be part of the Worldmappin Community and join our Discord Channel to get in touch with other travelers, ask questions or just be updated on our latest features.
Congratulations!
✅ Good job. Your post has been appreciated and has received support from CHESS BROTHERS ♔ 💪
♟ We invite you to use our hashtag #chessbrothers and learn more about us.
♟♟ You can also reach us on our Discord server and promote your posts there.
♟♟♟ Consider joining our curation trail so we work as a team and you get rewards automatically.
♞♟ Check out our @chessbrotherspro account to learn about the curation process carried out daily by our team.
🏅 If you want to earn profits with your HP delegation and support our project, we invite you to join the Master Investor plan. Here you can learn how to do it.
Kindly
The CHESS BROTHERS team
This post has been shared on Reddit by @uwelang through the HivePosh initiative.
Glad you brought this up. this topic is a game-changer 👀