In this video I go over the natural exponential function y = ex and define it strictly from looking at the inverse of the natural logarithmic function y = ln(x). The natural exponential function is one of the most widely used and important function in all of mathematics so it is important to understand the definition of it.
Watch Video On:
- DTube: https://d.tube/#!/v/mes/wz4b4tjsk3b
- BitChute: https://www.bitchute.com/video/CcPnEoatbeSu/
- YouTube: https://youtu.be/vGsOA2eqkig
Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIg4QqF_gaw8_b_k3vCw?e=2s2TqK
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donateReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord chat room: https://mes.fm/chatroom
Check out my Reddit and Voat math forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
-- Try 4X+ speed by browser extensions or modifying source code.
-- Browser extension recommendation: https://mes.fm/videospeed-extension
-- See my tutorial to learn more: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
NOTE #2: If video volume is too low at any part of the video:
- Download this browser extension recommendation: https://mes.fm/volume-extension
The Natural Exponential Function y = ex
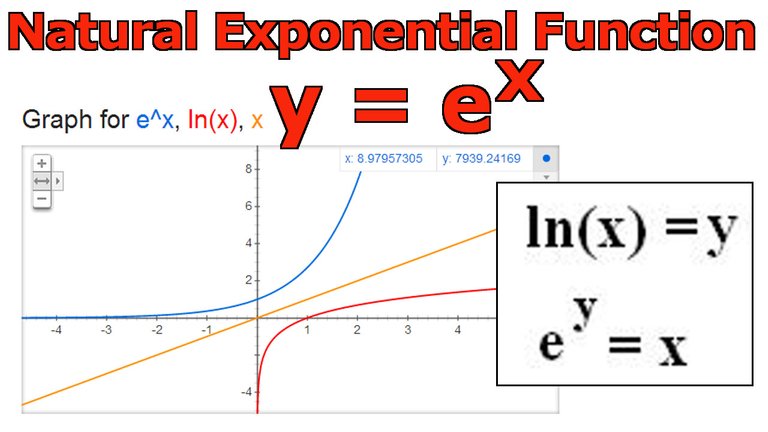
The natural exponential function y = ex derived from the natural logarithm function y = ln(x)

ln(x) is an increasing function thus it is a one-to-one function (i.e. each y-value has only 1 x-value)
Thus it has an inverse function (i.e. can switch or “invert” all data points from (x, y) to (y, x).
Let exp be the inverse of y = ln(x), in other words:

Recall the cancellation formulas:


Recall also the log law: If r is a rational number:

Taking into account all the above requirements for the inverse of ln(x), it leads us to define (even if x is irrational).

The natural exponential function, ex, is very important because it is used throughout calculus, engineering, etc.
