In this post, I had originally just wanted to share the following 2012 presentation on Quasicrystals by the theoretical physicist Paul Steinhardt. But after writing up the definitions and terms as context for the presentation, this post grew to include much more. From impossible tilings, impossible crystals, to ultimately impossible optical properties, the history of quasicrystals has been a history of the "impossible". However, these "impossible" properties may be more accurately labeled as "classified", as will be discussed further in this post.
Here is the great presentation on quasicrystals by Paul Steinhardt that was the driving force behind this post.
YouTube video: https://youtu.be/a0wo_yAh0Ps
Title: Paul Steinhardt on Impossible Crystals
Date: 22 June 2012
IMPORTANT NOTE: For some strange reason, the video is only allowed in Canada. So, I have downloaded the video and you can watch via my OneDrive link: https://1drv.ms/v/s!As32ynv0LoaIiY0I5xzfmlemCQgcmw?e=DD2RHn
Definition of terms
To give context to the presentation, here is a quick rundown of some of the terms involved.
- A quasicrystal or "quasiperiodic crystal" is a structure that is ordered but not periodic.
- Ordered = presence of symmetry.
- Periodic = repeating pattern.
- Quasicrystals display quasiperiodicity, which is irregular periodicity.
- A quasicrystalline pattern can continuously fill all available space (referred to as tiling), but it lacks translational symmetry.
- Translation is moving from one place to another without rotation.
- Tiling or tessellation is the covering of a surface (often called a plane) using 1+ geometric shapes (called tiles) with no overlaps or gaps.
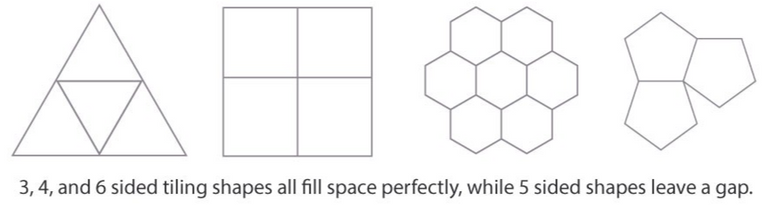
- Only 3 shapes can form 2D tilings with identical periodic tiles, translational symmetry, identical sides, AND the same interior angles: Equilateral triangles, squares, and hexagons.
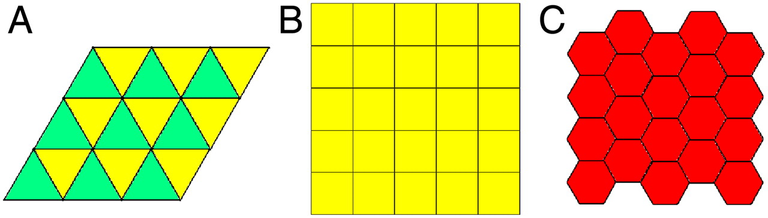
- Rotational symmetry is when a shape looks the same after a partial turn.
- If the rotation angle is 2π/n, then it is said to be n-fold.
- Note that 2π in radians is equivalent to 360 in degrees, that is 2π is a full rotation of a circle.
- This means that a rotational angle 2π/n will eventually return back to the starting position after n turns.
- An n-sided regular polygon (equal sides and share a common center) are n-fold.
- If the rotation angle is 2π/n, then it is said to be n-fold.
- According to the crystallographic restriction theorem, any single rotational shape that tiles the plane must have either 2-fold, 3-fold, 4-fold, or 6-fold symmetry.
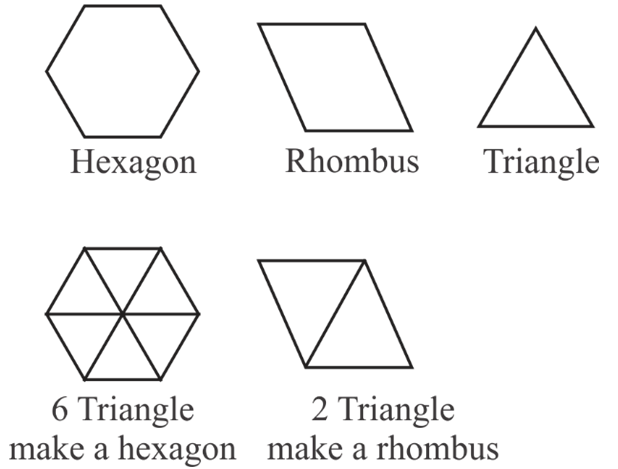
- Note that a rhombus and a rectangle both have 2-fold symmetry and can tile the plane.
- A rhombus can be viewed as comprising 2 equilateral triangles.
- A rectangle can be viewed as comprising 2+ squares.
- Note that a rhombus and a rectangle both have 2-fold symmetry and can tile the plane.
- The problem arises when trying to tile the plane with "forbidden" fold-symmetry, such as 5-fold symmetry.
- For example, a pentagon can't tile the plane because it always forms a gap that doesn't match it's internal angles.
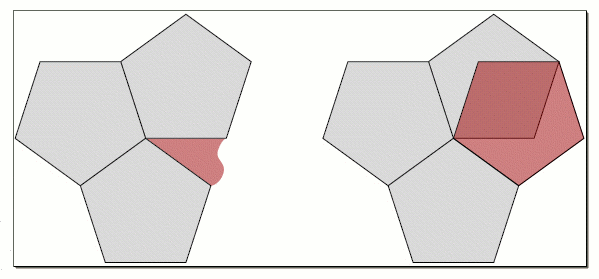
- The limited geometry of periodic tiling has given rise to aperiodic tiling.
- Aperiodic tiling is a non-periodic tiling (that doesn't have a repeating pattern) but also an additional property that it doesn't contain any arbitrarily large periodic regions.
- Aperiodic means that shifting the tiling by any finite distance, without rotation, cannot produce the same tiling.
- These are formed by using a specific set of tiles (called prototiles) and constructed using a specific set of rules.
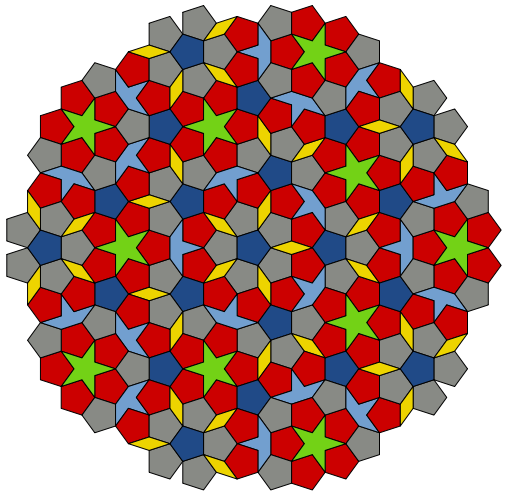
- The Penrose tilings are the best-known examples of aperiodic tilings.
- These are named after Roger Penrose, who investigated them in the 1970s.
- Penrose tilings have a 5-fold rotational symmetry and a reflection symmetry (have a mirror image across an axis).
- The original Penrose tiling was made up of the following prototiles:
- Pentagon
- Pentagram: a 5-pointed "star".
- "Boat": roughly 3/5 of a star.
- "Diamond": a thin rhombus
- The tiling construction involves "matching rules" that specify how tiles meet each other.
- The pentagon tiles involve 3 different matching rules, hence treating these as separate prototiles gives a set of 6 prototiles overall.
- Penrose further refined the above tiling to instead use just 2 tilings.
- The main rule for constructing the tiling is to match up the inscribed curves such that they are always continuous (including forming a closed circle).
- The possible tile connections are shown below:
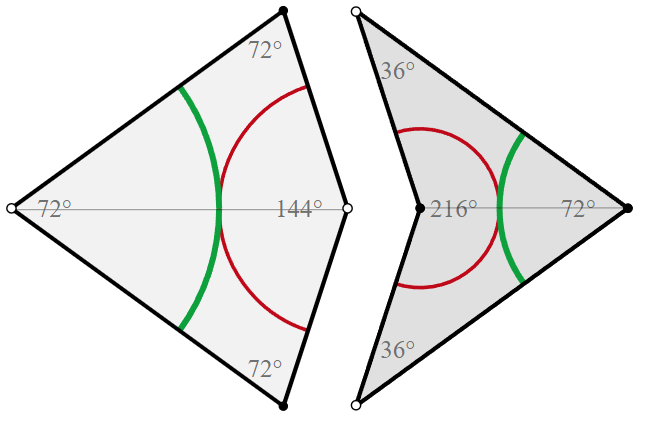
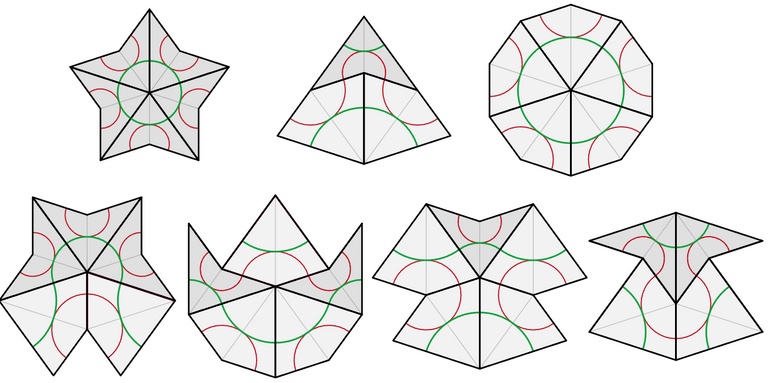

- The aperiodic tiling patterns had previously been thought to be impossible both mathematically and in nature.
- For more information, see the following paper:
- URL: https://www.physics.princeton.edu/~steinh/Lincei.pdf
- Title: Quasicrystals: a brief history of the impossible
- Author: Paul J. Steinhardt
- Published: 15 September 2012
- Once they were confirmed to exist mathematically, there was a hunt to see if these patterns existed in nature.
- The 2D mathematical tilings can be expanded to the 3D world (and to even higher dimensions).
- For more information, see the following paper:
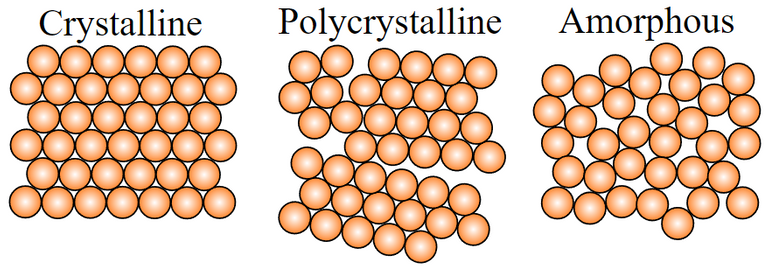
- Natural crystals have long been thought to only exist as either highly periodic structures or highly disordered (amorphous or glassy) structures.

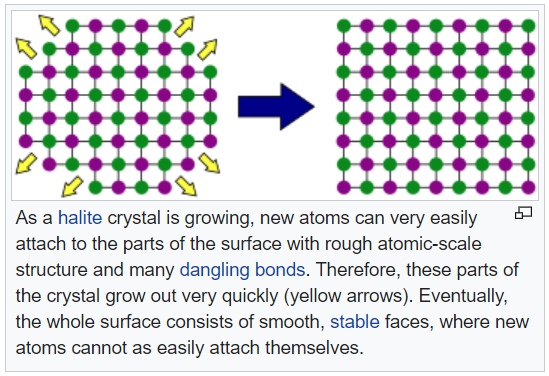
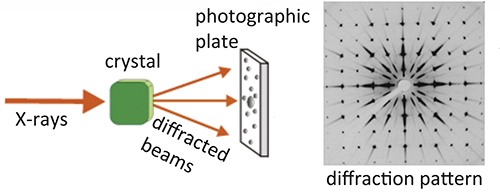
- The structure of a crystal can be deduced by X-ray or electron diffraction, which involves shining X-rays at the crystal and capturing the resulting diffracted patterns.
- Learn more here: https://www.xtal.iqfr.csic.es/Cristalografia/parte_02-en.html
- This is essentially seeing the crystal's shadow.

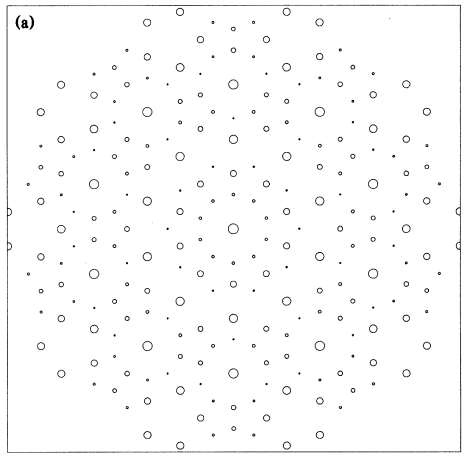
- In 1984, Dov Levine and Paul Steinhardt modeled the expected X-Ray diffraction pattern for a crystal with a symmetric but aperiodic pattern, i.e. a quasicrystal.
- URL: https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.53.2477
- Title: Quasicrystals: A New Class of Ordered Structures
- Authors: Dov Levine and Paul Joseph Steinhardt
- Published 24 December 1984
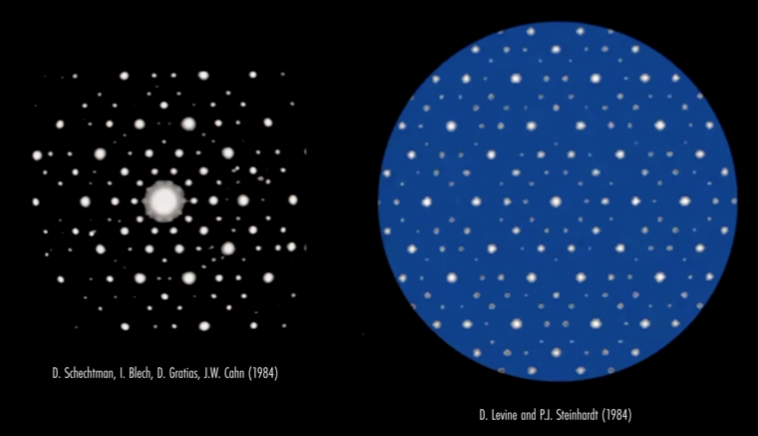
- In that same year, Dan Shechtman and his team published a paper detailing the structure of a rapidly cooled alluminum alloy forming the same quasicrystal electron diffraction gradient.
- URL: https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.53.1951
- Title: Metallic Phase with Long-Range Orientational Order and No Translational Symmetry
- Authors: D. Shechtman, I. Blech, D. Gratias, J.W. Cahn.
- Date Published: 12 November 1984


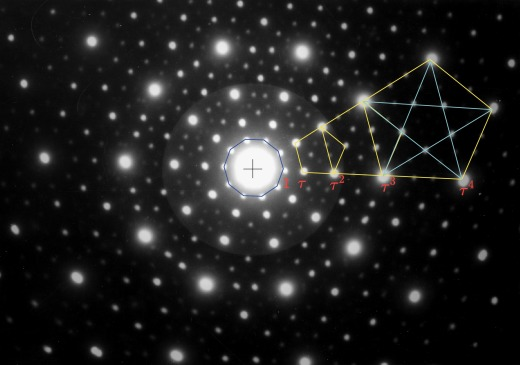
- The pentagonal symmetry can be seen in the diffraction pattern, taken from the following paper:
- URL: https://www.sciencedirect.com/science/article/pii/S1631070519300386
- Title: Discovery of quasicrystals: The early days
- Authors: Denis Gratias and Marianne Quiquandon
- Published: 23 May 2019
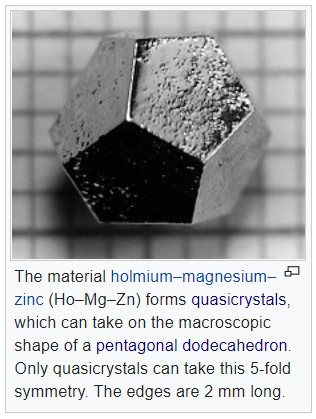
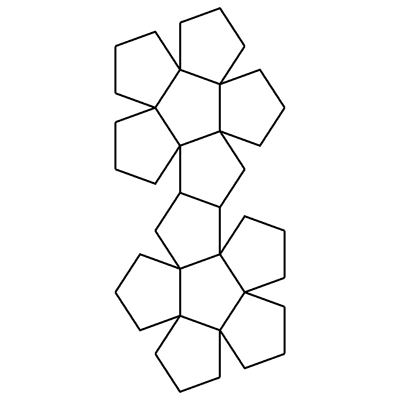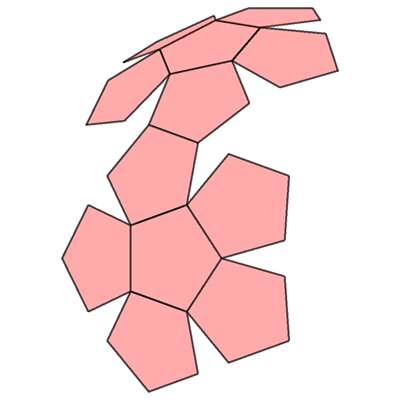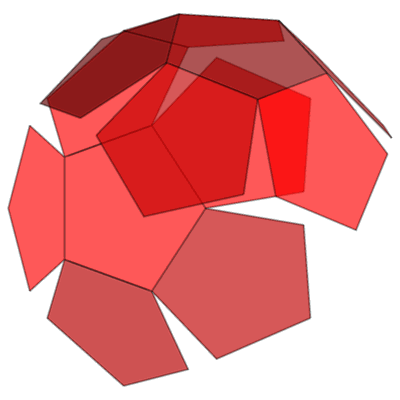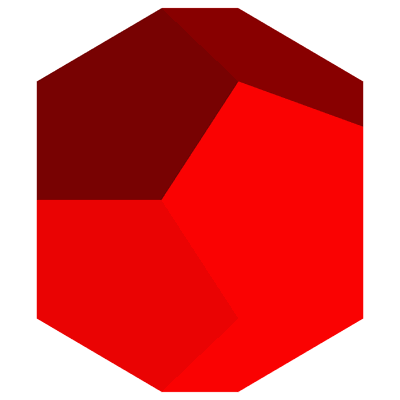
- A typical example of a quasicrystal is the alloy of holmium-magnesium-zinc (Ho-Mg-Zn) which can take up the macroscopic shape of a pentagonal dodecahedron.
- A regular or pentagonal dodecahedron has 12 regular pentagonal faces.


Recent video about Veritasium
Here is another great video going over the history and construction of a aperiodic tilings, as well as the many golden ratios present.
- URL: https://youtu.be/48sCx-wBs34
- Title: The Infinite Pattern That Never Repeats
- Published: 20 September 2020
1998 UFO Whistle Blower Edgar Fouché
Quasicrystals have potential applications in hardening steel, heat insulation, LEDs, hardening plastics, and even new materials that convert heat to electricity. But beyond even these applications is the high likelihood of advanced "classified" applications.
To grasp this, consider the (public) timeline of quasicrystal history.
- 1982: Dan Shechtman first observed quasicrystal structures using electron diffraction.
- 1983: Paul Steinhardt first demonstrated a mathematical concept of quasicrystals in a patent disclosure.
- 1984: Dan Shechtman published his findings on quasicrystal structures.
- 1984: Paul Steinhardt published his complete mathematical theory on quasicrystals and modeled the expected diffraction patterns.
- 1982 to 1987: Dan Shechtman was mocked for his quasicrystal claims, even being called a "quasi-scientist".
- 1987: First X-ray diffraction of a quasicrystal was produced.
- Note that X-ray diffraction requires much larger crystals than does electron diffraction.
- 1992: Definition of a crystal changed.
- Pre-1992: A crystal is a solid composed of atoms arranged in a periodic pattern in 3 dimensions.
- 1992: A crystal is a solid having an essentially discrete diffraction diagram, and an aperiodic crystal is any crystal that doesn't have a 3D periodic lattice.
- 1994: Linus Pauling, 2-time Nobel Laureate and the biggest critic of quasicrystals, dies at the age 1993.
- Even until his death, Linus argued that quasicrystals don't exist in nature, but are rather just smaller parts of bigger periodic crystals.
- 2009: The first natural quasicrystals were discovered.
- 2011: Dan Shechtman wins the Nobel Prize in Chemistry for his work on Quasicrystals.
- Dan's Nobel prize presentation and lecture can be seen here: https://www.nobelprize.org/prizes/chemistry/2011/shechtman/lecture/
- His lecture Power Point slides can be downloaded here: https://www.nobelprize.org/uploads/2018/06/shechtman-lecture_slides.pdf
Thus, to summarize: quasicrystals were mathematically and physically discovered in the early 1980s, rejected until the late 1980s, found in nature in the late 2000s, and obtained Nobel Prize recognition in the early 2010s.
This now brings us to a man by the name of Edgar Rothschild Fouché.

Edgar Fouché joined the US Air Force in 1967 and was selected for the Pararescue field, which involves recovery and medical treatment of personnel in humanitarian and combat environments. After an injury, he was retrained as an electronics and cryptographic specialist. His growing skillset allowed him to obtain a top secret cryptography clearance. After which he worked for about 20 years in the US military and another decade working for defense contractors across many levels of the military.
In the mid-1970s he worked at the top secret Nevada Test Site, otherwise known as Area 51. It was at this time that he worked directly with advanced digital technologies well ahead of what the public was aware to be possible.
In the early 1990s, along with a few close friends he worked with, decided that they were going to disclose to the public of the advanced technology that the US government has been holding back under the guise of "classified" technology.
In 1998, he made his first public presentation disclosing his life and work. In that same year he also co-written and published a book called "Alien Rapture - The Chosen"; which is a fictionalized disclosure of his life with names / places obscured to avoid legal ramifications.

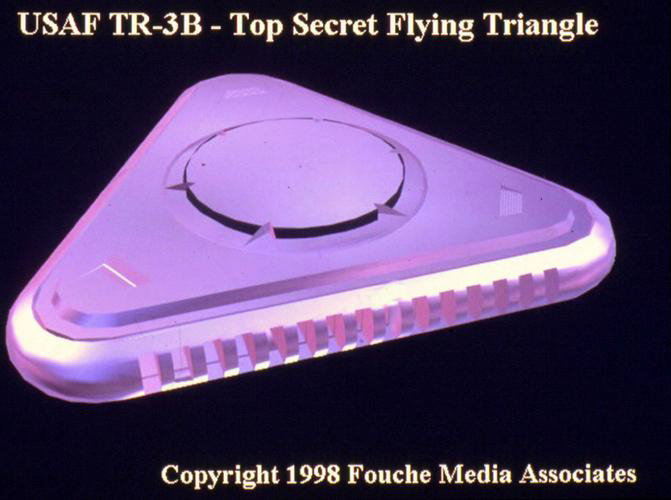
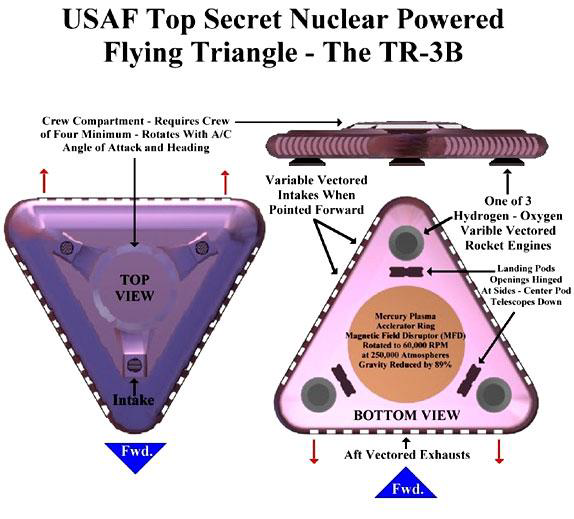
In Edgar's presentation and book, he stated that we worked with and was given knowledge of advanced propulsion, electromagnetic, and computing technologies. Of particular interest is that he specifically mentioned hearing the phrase "quasicrystals" being used in 1979 as a coating on the famous TR-3B triangular anti-gravitic space craft. This is several years before the publicly acknowledged discovery of quasicrystals. Even Edgar's 1998 disclosure presentation was during a time when quasicrystals were not (publicly) well understood.
This disclosure raises a lot of questions, not just about how far classified technology has gotten today, but what "classified reality" may actually be...

Links and sources relating to Edgar Fouché
The links to Edgar's life, work, and death are listed below.
- Obituary: https://www.masonfuneralhome.net/obituary/4251987
- Born: 22 February 1948
- Died: 11 May 2017
- Note that his name is written as "Edgar Albert Fouché" and no mention is made of his top secret disclosures.
- IMDb profile: https://www.imdb.com/name/nm8053473/bio
- Andrew Johnson's book:** Finding the Secret Space Programme: https://www.checktheevidence.com/wordpress/2018/05/31/book-finding-the-secret-space-programme/
- Ed's 1998 book: Alien Rapture: https://www.amazon.ca/Alien-Rapture-Rothschild-Steiger-Paperback/dp/B00YRBZ8TQ
- Expopaedia profile: https://www.exopaedia.org/Fouche%2C+Edgar
- Edgar Fouché interview series with Andrew Johnson: https://www.youtube.com/playlist?list=PLX_9c2xy6YwHPdlFs15KtpTPm2CzSzc72
- Archive of his now-outdated website FoucheMedia.com: http://web.archive.org/web/19990220030136/http://www.fouchemedia.com/
- FOIA documents confirm Ed's life details: https://www.checktheevidence.com/wordpress/2015/01/13/edgar-fouche-documents-released-in-foia-show-the-same-type-of-record-as-he-provided-himself/
- Ed's 1998 Full Presentation video:
- Presentation notes: https://checktheevidencecom.ipage.com/checktheevidence.com/pdf/Edgar%20Fouche%20-%201998%20Presentation%20to%20IUFOC.pdf
- Specific clip about quasicrystals:
- Wolf Clan Media's article: 9/11 Optical Illusions: https://wolfclanmedia-research.blogspot.com/2017/12/optical-illusions-on-911.html
- Hive blockchain version: https://peakd.com/hive-113182/@mes/911-optical-illusions-hive-113182
- Wolf Clan Media interview with Andrew Johnson:
- National Institute of Standards and Technology (NIST) profile: https://www.nist.gov/nist-and-nobel/dan-shechtman/person-behind-nobel-prize-dan-shechtman
More Images of the TR-3B Flying Triangle
For future reference, I have included a collection of the images of the TR-3B found in Edgar Fouché's presentation lecture notes.






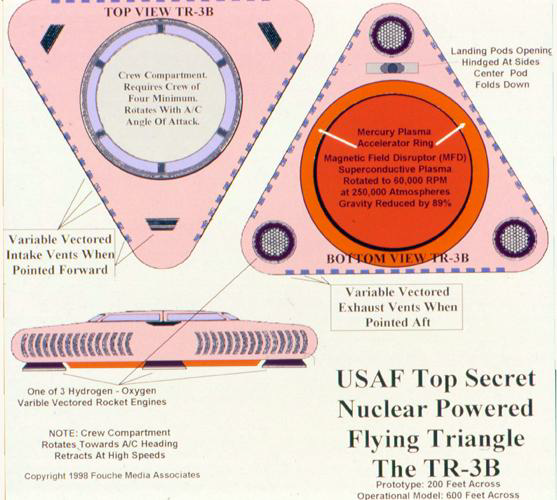

Optical Cloaking with Quasicrystals and Metamaterials
Edgar Fouché had stated that quasicrystals were used in the outer skin of the TR-3B. This brings our attention to a 2015 paper by Svetlana Boriskina on the potential use of quasicrystals in optical cloaking, in other words, invisibility technology.
URL: https://www.researchgate.net/publication/279886421_Quasicrystals_Making_invisible_materials
PDF: https://arxiv.org/ftp/arxiv/papers/1604/1604.08124.pdf
Title: Quasicrystals: Making invisible materials
Author: Svetlana V. Boriskina
Published: 30 June 2015
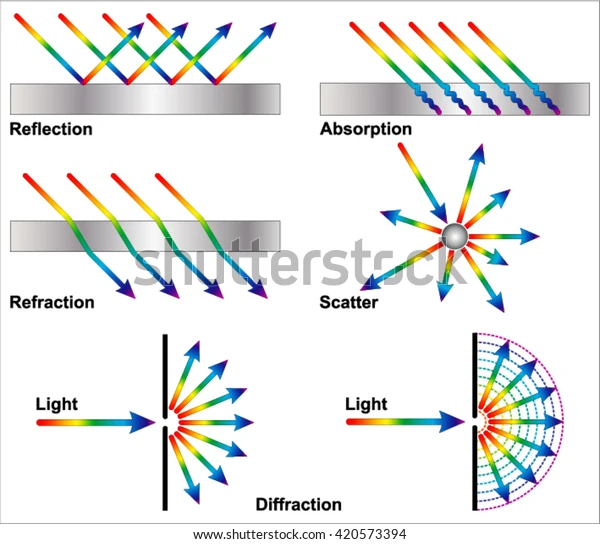
The basis of optical cloaking involves the properties of refraction. Firstly, note the difference between refraction, diffraction, and other types of light phenomena.
- Refraction is the change in the angle of light through a material due to the change in the speed of light in the material.
- Reflection is light reflecting back at the same angle, like a mirror.
- Absorption is light getting absorbed into the material.
- Scattering is light getting absorbed a material before emitting other light in all directions.
- Diffraction is the bending of light around an object or through an opening.
An animation of refraction is shown below.

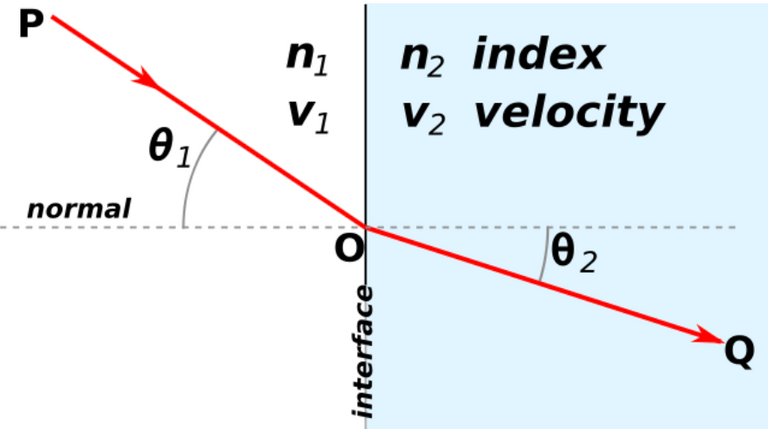

The refractive index, n, is given by the formula:
n = c / v
where:
- c = speed of light in a vacuum.
- v = phase velocity of light in the material.
- The phase velocity is the speed of the crests of the wave.
- This may be different than the group velocity, which is the speed at which a pulse of light moves.
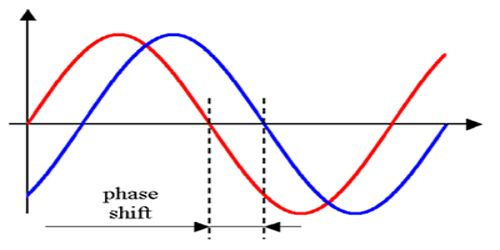
Note that the "phase" of a wave is an arbitrary starting point of the cycle of a wave. This becomes important when dealing with multiple waves, since 2 of the exact same waves can still differ by phase.
Natural materials have only been shown to have "positive" refraction, which is a deflection of light that is ultimately still in the forward direction. Man-made materials with a "negative" refraction angle have recently been shown to be possible. In general, man-made materials that display properties not found in nature are called metamaterials.
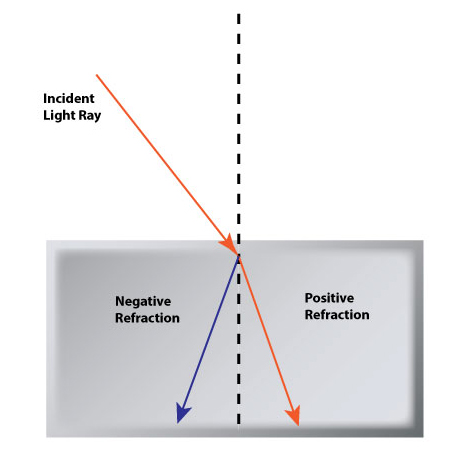
Light bends the "wrong" way in negative refraction.

Simulated image of a negative-index refraction (right)
Negative-index metamaterials (NIM) are made possible by designing microstructures smaller than the wavelength of the incident light, allowing for bizarre effects.
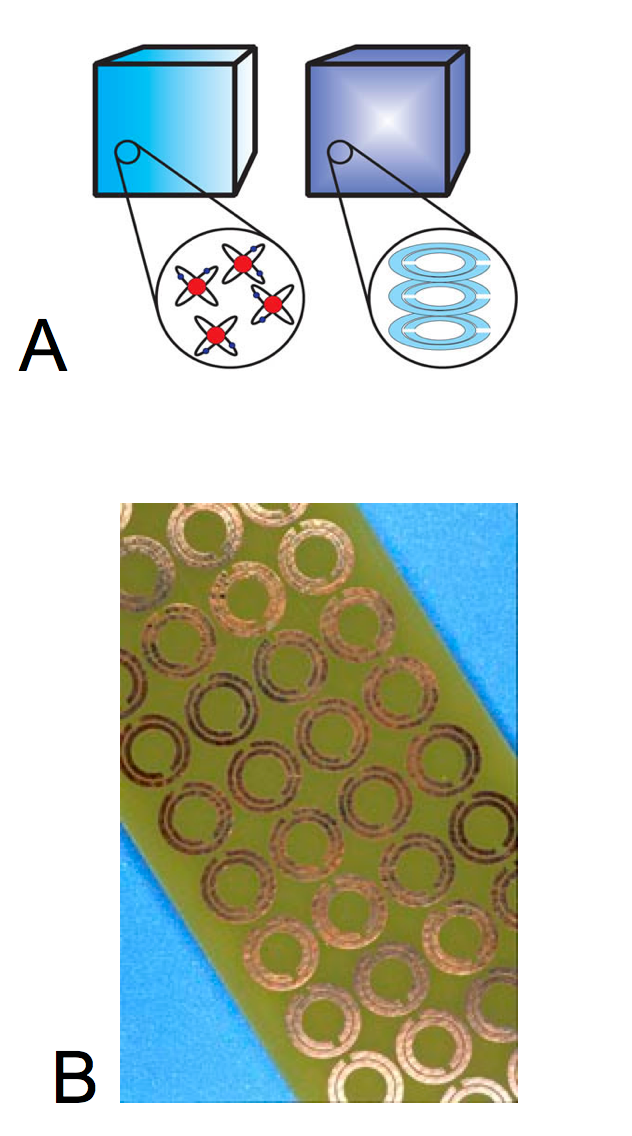

Now, going back to the formula for the refractive index, n = c/v. If the wavelength of the wave in the medium is increased to become very large, near infinity, then the phase velocity goes to infinity as well. This means that the index n approaches 0 since we are dividing c / ( near infinity). What we get in this case is a metamaterial with a "zero-index" of refraction. Effectively, this means light gets stretched across the medium, until it exits just as it entered.

Compare the different behavior of light traveling from 2 materials with their corresponding refractive-indices.
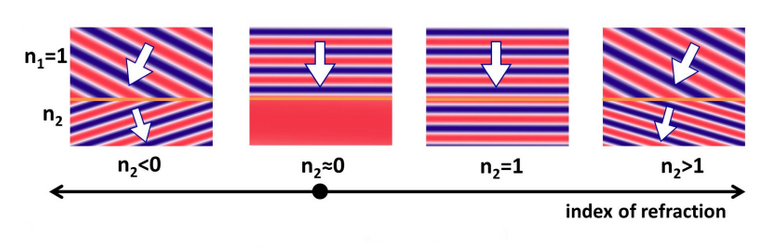
With a zero-index metamaterial, it is theoretically possible to direct light at an angle without typical deflection and distortion.
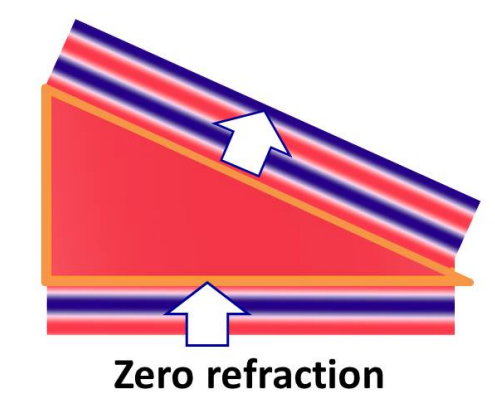
This raises the possibility of a literal invisibility shield, which stretches light around an object until it exits the other end, thus cloaking the object inside.
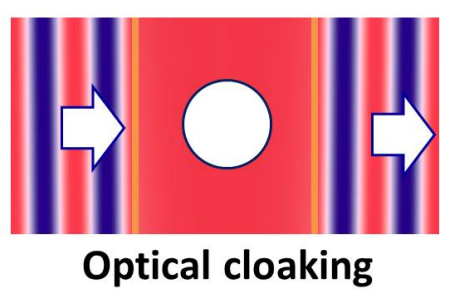
Let's summarize again: Edgar Fouché said in 1998 that he overheard that quasicrystals were being used on the skin of an anti-gravity TR-3B spacecraft in the 1970s and earlier. Quasicrystals were publicly disclosed in the early 1980s, ridiculed until the early 1990s, and in the 2010s the possibility of optical cloaking was being proposed.
If I put on my tinfoil hat, which I am a proud wearer, I think it is likely that quasicrystals had some invisibility applications on the TR-3B, and other classified technology...
For reference, I have include links to several sources which I used in the writeup of this metamaterial section.
Wiki: https://en.wikipedia.org/wiki/Negative-index_metamaterial
Title: Negative-index metamaterial
URL: https://faculty.washington.edu/goussiou/486_W15/Harvey_NIM.pdf
Title: Negative-Index Metamaterials
Author: Sarah Harvey
Published: 9 February 2014
Video: https://youtu.be/KPKGVkYLtfE
Title: How Light Behaves When The Refractive Index Vanishes - CLEO 2020 Science and Technology Tutorial
Author: Robert Boyd
Published: 4 June 2020
Video: https://youtu.be/ogNKrQCH1Kk
Title: The Schrödinger lecture 2012 - Metamaterials: new horizons in electromagnetism
Author: Sir John Pendry
Published: 9 November 2012
Lecture promotion: https://www.imperial.ac.uk/events/110202/metamaterials-new-horizons-in-electromagnetism/
2003 Grant application: https://gow.epsrc.ukri.org/NGBOViewGrant.aspx?GrantRef=GR/S49537/01
URL: https://physicsworld.com/a/silicon-waveguide-shows-zero-refractive-index/
Title: Silicon waveguide shows zero refractive index
Author: Edwin Cartlidge
Published: 25 October 2017
!1UP
You have received a 1UP from @luizeba!
@stem-curatorAnd they will bring !PIZZA 🍕
Learn more about our delegation service to earn daily rewards. Join the family on Discord.