OR: Lies, Damned Lies, Statistics, Data Science & Rankings?
Initially, the reason why I was posting this primarily in a gaming venue was because, in many of our games, rankings are critical not only to bragging rights -- but to hundreds of dollars of monthly rewards. Yet, it is frequently true that rankings (and rewards) are heavily swayed by factors other than player skill (and, of course, the unavoidable vagaries of Lady Luck). The best example of this is Splinterlands bot-friendly top 50 before the dual fix of 1) not rounding win scores below 10 up to 10 and 2) not doubling scores for winning streaks, a player has reached Champion I.
It was only as I was writing this article, however, that I realized that if this fix had been applied globally, it would have totally prevented the bot flood problem and the exodus of a lot of value from Splinterlands. While I was previously convinced that the Collection Power is ABSOLUTELY NECESSARY for Splinterlands, I really should have titled the article Why a Bot Flood Fix is ABSOLUTELY NECESSARY for Splinterlands. Given this much simpler fix (or a second even simpler and less invasive one that I detail near the bottom of the post), I would now argue that implementing collection power instead would be a huge mistake given its numerous drawbacks (programming/implementation time, making many players unhappy, giving even more of an impression of being pay-to-play, no guarantee that it will actually work, etc.) and no real advantages.

I'm actually going to go through the thought processes that led to these conclusions (rather than just summarizing only the salient ones) because a) there were a lot of interesting points along the way; b) I want to make a number of points about bad data science; c) as I continue to enhance it, I'm still coming up with good Splinterlands ideas (like two different solutions that are better than collection power) and d) I'd hate to throw all my awesome writing away 😜). People who aren't interested in all this *cough*great stuff*cough* can just jump to the Splinterlands logo near the bottom for the conclusions and a call to action. Note that, despite the possibly scary reference to data science, this article does NOT require any knowledge of statistics past what a bell curve (such as the one theoretically used for school grades) looks like -- just common sense.
This all started when I ran across a really great 2017 Towards Data Science Medium article entitled Napoleon was the Best General Ever, and the Math Proves it with the subtitle Ranking Every* General in the History of Warfare. It is chock full of interesting facts and history -- even if I would call the "math" by which the conclusion was reached abysmally incorrect. If you're at all interested, you should go and read it -- and see if you can come up with what I disagree with -- before you continue.
The author goes to a lot of work to collect battle data from Wikipedia to produce the following, seemingly slam-dunk chart:
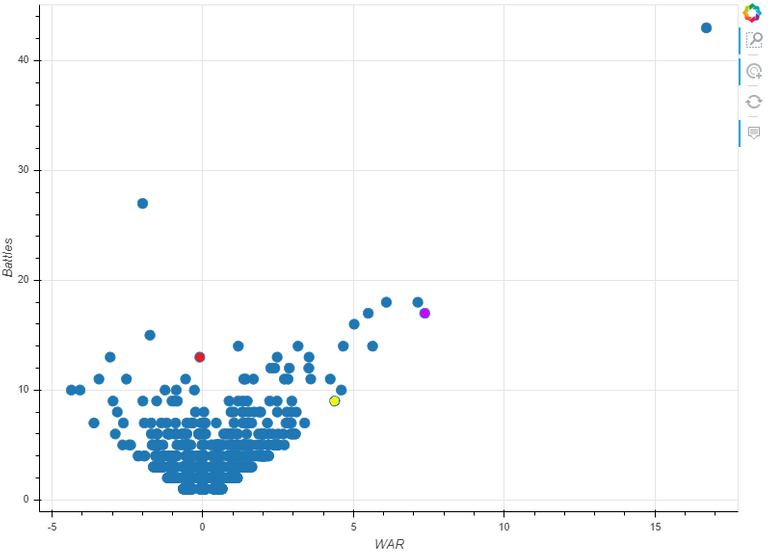
The dot in the upper-right is, obviously, Napoleon with Washington, Caesar and Alexander the Great represented by the red, blue and yellow dots respectively. The second highest dot towards the left is Robert E. Lee. An interactive visualization allows you to hover over any of the dots and view the general's name, number of battles, score and score per battle.
If you haven't already figured out the flaw in the article's data analysis, take some time to look at both what the graph shows and what you expect to see. You might also want to ignore the outliers of Napoleon and Lee (hint: who are over-represented in the battle data set). See if you can spot regularities and logically expected results like generals with better scores have more battles -- because who would continue to use a bad general (assuming that he survived)? Also note what do you not see, like randomness or the bell curve of a normal distribution. And do you really believe that Napoleon's skill was as far removed above that of Caesar and Alexander the Great as the chart indicates?
Good visualizations tell great stories even without needing to look at all the numbers behind them. The first thing to note is that the bottom of the data point cloud can be defined by two lines with that converge at 0, -0.5 (due to how the individual battle scores are calculated against an average "replacement" general). Since our data set has a reasonable amount of data points, these lines demarcate the best and worst possible performance scores for generals. Now, do you see the problem here?
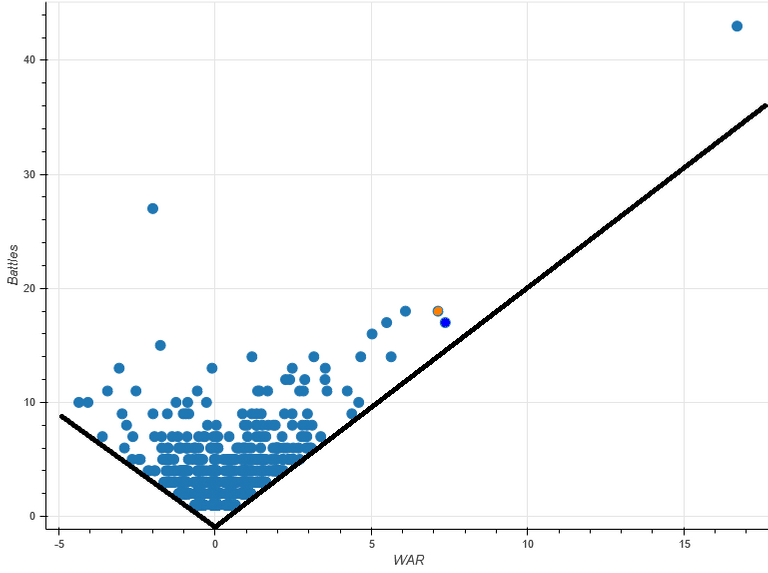
The best/worst possible scores are entirely dependent upon the number of battles fought. This grossly exaggerates the positive or negative score of a generals with a large number of battles. Lee made mistakes like Pickett's Charge but, overall, he was a better than average general with a worse than average army -- not in the bottom 20% as his score would indicate. Similarly, Napoleon's score is insanely high even though, percentage-wise, he is actually further from the best possible score line than several other generals -- including his ultimate nemesis, Arthur Wellesley, the First Duke of Wellington (the orange dot just above and to the left of Caesar's blue).
Looking at the method by which the score is calculated explains this result perfectly. A general's score is simply the sum of all of his individual battle scores. Why the analyst (I refuse to call him a data scientist) chose this metric can probably be laid at the door of it proving his initial belief (i.e. confirmation bias). Clearly, a much more rational metric would be a general's average battle score (subject to a certain minimum number of battles).
ELO scores would have been even better -- if there had been a sufficient number of battles between generals and they weren't separated into groups based upon time period. Also, of course, assuming that the change in ranking isn't modified to mess with the average of all rankings by . . . oh . . . say . . . rounding low scores up to 10 and doubling the change if the general is on a winning streak. Normal ELO scores don't change the average ranking of all ranked individuals -- and thus, don't lead to score inflation due to number of wins (as is the case with Napoleon). In contrast, The Splinterlands ELO modifications increases all rankings so radically that player's ranks need to be automatically dropped 25% or more at the end of each 15-day season.
I assume that everyone recognizes Augustus Caesar. Iosif Vladimirovich Gurko's claim to fame was due to his spearheading of the Russian invasion in the Turkish war in the latter half of 1877. According to Wikipedia, Korean Admiral Yi Over the course of his career, Admiral Yi fought in at least 23 recorded naval engagements in the late 1500s, most where he was outnumbered and lacked necessary supplies. His most famous victory occurred at the Battle of Myeongnyang, where despite being outnumbered 133 warships to 13, he managed to disable or destroy 31 of the 133 Japanese warships without losing a single ship of his own.
Astute readers will have noticed that the scores of those with fewer battles are now higher ranked than those with more battles. This is due to selection bias (in the data and thus not the analyst's fault -- except that than he should have recognized it and called it out in his analysis). Individual battle scores were modified according to how difficult an average "replacement" general would have found it to win. This meant that glorious underdog victories would generally add substantially to a general's score while a win with overwhelming odds on your side would add little to a general's score and could easily lower his average.
The selection bias comes about due to the fact that glorious underdog victories are far more likely to be remembered than run-of-the-mill overwhelming victories. For example, note that fact that Wikipedia says that Admiral Yi fought in at least 23 recorded battles -- yet only 5 appear inthis dataset. Adjusting for this fact puts Napoleon right back in the running for best general with the margin of error allowing any of the top 3 to arguably be the winner as well.
Another serious shortcoming in the analysis is that it doesn't take into account if the enemy general is substantially better than average. For example, many of Lee's repeat opponents have Average Battle Scores far above the mean -- particularly his most common match-up, Ulysses S. Grant. If Lee had average foes, it is highly likely that his score would have been positive rather than negative.
There is also the problem of intangibles and other factors that can have a significant impact on the battle, such as morale as well as quality and condition of troops. It is much easier for a well-supplied general currently on winning side with rested high-quality veteran troops (or even elite mercenaries like Swiss pikemen) than for a general whose troops (or peasant levies) are reeling from repeated losses, poor supplies and constant turn-over. On the other hand, for many more recent battles, this type of information is available to a major extent and it could have been factored in.

So, let's get back to Splinterlands since I've probably gone on for far too long; however, the above does thoroughly demonstrate the problems that arise when people do simplistic or partial analyses and proclaim "the Math Proves it". It also demonstrates the pitfalls of chosing to disdain tried and true methods (and average score is pretty obvious) in favor of developing "brilliant" new methods and expecting that these untried, untested solutions will always be an improvement and problem-free. Not to mention, that it's common and really bad to see someone provide a great visualization and somehow not notice when it clearly shows that their analysis has problems -- or when their method has known and acknowledged problems and they don't analyze them, determine their true source and correctly solve them.
Now, it is not always easy to track down the source of a problem. Indeed, many programmers often avoid he effort and apply fixes or "kludges" that correct the known appearances of problems rather than the actual source of those problems. And, almost invariably, this intellectual laziness comes back to bite them as the problem continues to manifest in unanticipated ways (unanticipated because they have no clue of what the problem is to anticipate from) or because their kludges generate problems of their own. It is also well known that kludges invariably involve more, and most often substandard and repetitive, code which turns into technical debt and a nightmare for maintenance and future improvement.


Splinterlands demonstrates exactly these problems. The modifications to ELO that the Splinterlands team made are entirely to blame for the bot flood. Worse, even after realizing that these modifications were problematical (when they removed them to solve the problem of subpar bots who could steal top 50 spots by playing far more games than human players could or would match), they chose not to apply the solution globally -- presumably because they didn't check to see if it was causing other problems elsewhere (such as the bot flood). Instead, once it was obvious that the bot flood had to be fixed, they quickly decided to implement the more expensive and disadvantageous collection power fix.
Now, again, I'll emphasize that the source of problems aren't always easy to track down. I didn't realize that the ELO modifications were the source of the bot flood until I was writing this article. On the other hand, I wasn't involved in designing the Champion I/top 50 fix and thereby had the disadvantages of a modified ELO repeatedly beaten into my skull. If had been involved, I certainly would have looked at where I wasn't implementing the fix to see if it was causing problems there (it's just what good systems engineers do as a matter of course).

So let's look at the ELO modifications in the same way that we analyzed the Best General argument above. It is extremely obvious (and acknowledged) that rankings almost constantly rise in Splinterlands. Indeed, as mentioned above, the Splinterlands ELO modifications increases all rankings so radically that player's ranks need to be automatically dropped 25% or more at the end of each 15-day season. Now, I must acknowledge that always advancing is positive reinforcement which could be desired -- but I would also argue that it actually quickly turns hollow. The real goal is reaching higher levels as your skill improves, not mindlessly advancing because you've played more games (and then regularly being set back so that you can advance again).
Standard ELO does NOT increase the score of the winner by more than it decreases the score of the loser. Thus, the average ranking of all players doesn't constantly increase with the number of games played. And, most importantly, bots (and poor players) can't reach ridiculous levels because "a rising tide lifts all boats"
Before Splinterlands implemented its Champion I fixes, there were many more bots in the top 50 due to the fact that increased rankings were guaranteed by a greater number of wins. If the bot wasn't advancing, it was driving up the rankings of its competitors until it could advance. And this was entirely despite the fact that the bot's win percentage was 100% consistently significantly below that of comparably ranked players (or, statistically, there was far more covariance between number of games and ranking than there should have been). A good simple graph would have made this obvious (and even told you how many games a player had to play for a given win percentage to get to a desired ranking). And, I'll certainly commend the Splinterlands for recognizing and applying the correct fix.
Now, it must be noted that the bot flood problem wasn't quite as obvious at this point -- but it had been noticed. Why the team didn't immediately recognize that globally applying the ELO modification removal would have fixed that problem as well is beyond me. There is also the fact that recently solving a problem with a similar cause should have brought the same fix to mind when the bot flood problem did become urgent.

So, once the source of the problem is clear, we stand a chance of finding a good solution rather than a kludge. The obvious solution is to just remove the ELO modifications globally. This does, however, have side effects which do dramatically alter the ranking tempo of the game (the previously mentioned cycle of always advancing and then being dropped) in a way that may not be desired (but which I believe to be beneficial rather than detrimental).
But there is actually a second factor causing the problem whose solution causes much fewer such visible effects. The problem really isn't that rankings as constantly rising within seasons but that they are rising across seasons as well (until you hit the unmodified ELO wall at Champion I). If the real problem is that the cross-season average ranking is constantly rising, can't it just be fixed by ensuring that the seasonal reset always returns it to the same desired base level? At the end of the season, it would be trivial to calculate the average ranking and reduce everyone by the same factor necessary to return the average ranking to its desired value.
Both of these solutions have their relative pros and cons (the latter of which can frequently be prevented or ameliorated). If Splinterlands reverts to a straight ELO, ratings wouldn't have to be reset at the end of each season -- but then seasonal rewards would need to be made contingent upon a player playing at least a certain number of games). As an untried solution, relying solely on changing the seasonal reset may not be enough to completely solve the problem.
Fortunately, there is another incredibly minor set of changes that would be an improvement to both solutions and would be great preparation for when there are many more players in Splinterlands. Splinterlands already calculates and displays the exact position/placement of every player in the top 100. Why not do that for everyone? You could even base league and tournaments on Top X or Top X% rather than set rankings. This would easily allow all sorts of other simple adjustments as Splinterlands grows.
So . . . what am I missing this time? Are there any other concerns left? Or should we all speak up and try to get the Splinterlands team to reverse course? Please respond in the comments below.

It was only as I was writing this article, however, that I realized that if this fix had been applied globally, it would have totally prevented the bot flood problem and the exodus of a lot of value from Splinterlands. While I was previously convinced that the Collection Power is ABSOLUTELY NECESSARY for Splinterlands, I really should have titled the article Why a Bot Flood Fix is ABSOLUTELY NECESSARY for Splinterlands. Given this much simpler fix (or a second even simpler and less invasive one that I detail near the bottom of the post), I would now argue that implementing collection power instead would be a huge mistake given its numerous drawbacks (programming/implementation time, making many players unhappy, giving even more of an impression of being pay-to-play, no guarantee that it will actually work, etc.) and no real advantages.

I'm actually going to go through the thought processes that led to these conclusions (rather than just summarizing only the salient ones) because a) there were a lot of interesting points along the way; b) I want to make a number of points about bad data science; c) as I continue to enhance it, I'm still coming up with good Splinterlands ideas (like two different solutions that are better than collection power) and d) I'd hate to throw all my awesome writing away 😜). People who aren't interested in all this *cough*great stuff*cough* can just jump to the Splinterlands logo near the bottom for the conclusions and a call to action. Note that, despite the possibly scary reference to data science, this article does NOT require any knowledge of statistics past what a bell curve (such as the one theoretically used for school grades) looks like -- just common sense.
This all started when I ran across a really great 2017 Towards Data Science Medium article entitled Napoleon was the Best General Ever, and the Math Proves it with the subtitle Ranking Every* General in the History of Warfare. It is chock full of interesting facts and history -- even if I would call the "math" by which the conclusion was reached abysmally incorrect. If you're at all interested, you should go and read it -- and see if you can come up with what I disagree with -- before you continue.
The author goes to a lot of work to collect battle data from Wikipedia to produce the following, seemingly slam-dunk chart:

The dot in the upper-right is, obviously, Napoleon with Washington, Caesar and Alexander the Great represented by the red, blue and yellow dots respectively. The second highest dot towards the left is Robert E. Lee. An interactive visualization allows you to hover over any of the dots and view the general's name, number of battles, score and score per battle.
If you haven't already figured out the flaw in the article's data analysis, take some time to look at both what the graph shows and what you expect to see. You might also want to ignore the outliers of Napoleon and Lee (hint: who are over-represented in the battle data set). See if you can spot regularities and logically expected results like generals with better scores have more battles -- because who would continue to use a bad general (assuming that he survived)? Also note what do you not see, like randomness or the bell curve of a normal distribution. And do you really believe that Napoleon's skill was as far removed above that of Caesar and Alexander the Great as the chart indicates?
Good visualizations tell great stories even without needing to look at all the numbers behind them. The first thing to note is that the bottom of the data point cloud can be defined by two lines with that converge at 0, -0.5 (due to how the individual battle scores are calculated against an average "replacement" general). Since our data set has a reasonable amount of data points, these lines demarcate the best and worst possible performance scores for generals. Now, do you see the problem here?

The best/worst possible scores are entirely dependent upon the number of battles fought. This grossly exaggerates the positive or negative score of a generals with a large number of battles. Lee made mistakes like Pickett's Charge but, overall, he was a better than average general with a worse than average army -- not in the bottom 20% as his score would indicate. Similarly, Napoleon's score is insanely high even though, percentage-wise, he is actually further from the best possible score line than several other generals -- including his ultimate nemesis, Arthur Wellesley, the First Duke of Wellington (the orange dot just above and to the left of Caesar's blue).
Looking at the method by which the score is calculated explains this result perfectly. A general's score is simply the sum of all of his individual battle scores. Why the analyst (I refuse to call him a data scientist) chose this metric can probably be laid at the door of it proving his initial belief (i.e. confirmation bias). Clearly, a much more rational metric would be a general's average battle score (subject to a certain minimum number of battles).
ELO scores would have been even better -- if there had been a sufficient number of battles between generals and they weren't separated into groups based upon time period. Also, of course, assuming that the change in ranking isn't modified to mess with the average of all rankings by . . . oh . . . say . . . rounding low scores up to 10 and doubling the change if the general is on a winning streak. Normal ELO scores don't change the average ranking of all ranked individuals -- and thus, don't lead to score inflation due to number of wins (as is the case with Napoleon). In contrast, The Splinterlands ELO modifications increases all rankings so radically that player's ranks need to be automatically dropped 25% or more at the end of each 15-day season.
Returning to our generals, by the average battle score metric, Napoleon still performs very well -- but he is, by no means, the "Best General Ever". Indeed, he doesn't even make the top 5, even if the field is limited to generals with 9 or more battles..
| Name | # of Battles | Total Score | Average Score/Battle |
|---|---|---|---|
| Alexander the Great | 9 | 4.376 | 0.486 |
| Georgy Zhukov | 10 | 4.596 | 0.460 |
| Julius Caesar | 17 | 7.365 | 0.433 |
| Khalid ibn al-Walid | 14 | 5.633 | 0.402 |
| Arthur Wellesley, 1st Duke of Wellington | 18 | 7.133 | 0.396 |
| Napoleon Bonaparte | 43 | 16.703 | 0.388 |
| Oda Nobunaga | 11 | 4.229 | 0.384 |
| Name | # of Battles | Total Score | Average Score/Battle |
|---|---|---|---|
| Augustus Caesar | 7 | 3.38 | 0.483 |
| Iosif Vladimirovich Gurko | 6 | 3.078 | 0.513 |
| Admiral Yi Sun-sin | 5 | 2.706 | 0.541 |
I assume that everyone recognizes Augustus Caesar. Iosif Vladimirovich Gurko's claim to fame was due to his spearheading of the Russian invasion in the Turkish war in the latter half of 1877. According to Wikipedia, Korean Admiral Yi Over the course of his career, Admiral Yi fought in at least 23 recorded naval engagements in the late 1500s, most where he was outnumbered and lacked necessary supplies. His most famous victory occurred at the Battle of Myeongnyang, where despite being outnumbered 133 warships to 13, he managed to disable or destroy 31 of the 133 Japanese warships without losing a single ship of his own.
Astute readers will have noticed that the scores of those with fewer battles are now higher ranked than those with more battles. This is due to selection bias (in the data and thus not the analyst's fault -- except that than he should have recognized it and called it out in his analysis). Individual battle scores were modified according to how difficult an average "replacement" general would have found it to win. This meant that glorious underdog victories would generally add substantially to a general's score while a win with overwhelming odds on your side would add little to a general's score and could easily lower his average.
The selection bias comes about due to the fact that glorious underdog victories are far more likely to be remembered than run-of-the-mill overwhelming victories. For example, note that fact that Wikipedia says that Admiral Yi fought in at least 23 recorded battles -- yet only 5 appear inthis dataset. Adjusting for this fact puts Napoleon right back in the running for best general with the margin of error allowing any of the top 3 to arguably be the winner as well.
| Name | # of Battles | Total Score | Average Score/Battle |
|---|---|---|---|
| Ulysses S. Grant | 16 | 5.023 | 0.314 |
| Robert E.Lee | 27 | -1.994 | -0.073 |
There is also the problem of intangibles and other factors that can have a significant impact on the battle, such as morale as well as quality and condition of troops. It is much easier for a well-supplied general currently on winning side with rested high-quality veteran troops (or even elite mercenaries like Swiss pikemen) than for a general whose troops (or peasant levies) are reeling from repeated losses, poor supplies and constant turn-over. On the other hand, for many more recent battles, this type of information is available to a major extent and it could have been factored in.

So, let's get back to Splinterlands since I've probably gone on for far too long; however, the above does thoroughly demonstrate the problems that arise when people do simplistic or partial analyses and proclaim "the Math Proves it". It also demonstrates the pitfalls of chosing to disdain tried and true methods (and average score is pretty obvious) in favor of developing "brilliant" new methods and expecting that these untried, untested solutions will always be an improvement and problem-free. Not to mention, that it's common and really bad to see someone provide a great visualization and somehow not notice when it clearly shows that their analysis has problems -- or when their method has known and acknowledged problems and they don't analyze them, determine their true source and correctly solve them.
Now, it is not always easy to track down the source of a problem. Indeed, many programmers often avoid he effort and apply fixes or "kludges" that correct the known appearances of problems rather than the actual source of those problems. And, almost invariably, this intellectual laziness comes back to bite them as the problem continues to manifest in unanticipated ways (unanticipated because they have no clue of what the problem is to anticipate from) or because their kludges generate problems of their own. It is also well known that kludges invariably involve more, and most often substandard and repetitive, code which turns into technical debt and a nightmare for maintenance and future improvement.

WHICH EVENTUALLY BUT VIRTUALLY ALWAYS LEADS TO

Splinterlands demonstrates exactly these problems. The modifications to ELO that the Splinterlands team made are entirely to blame for the bot flood. Worse, even after realizing that these modifications were problematical (when they removed them to solve the problem of subpar bots who could steal top 50 spots by playing far more games than human players could or would match), they chose not to apply the solution globally -- presumably because they didn't check to see if it was causing other problems elsewhere (such as the bot flood). Instead, once it was obvious that the bot flood had to be fixed, they quickly decided to implement the more expensive and disadvantageous collection power fix.
Now, again, I'll emphasize that the source of problems aren't always easy to track down. I didn't realize that the ELO modifications were the source of the bot flood until I was writing this article. On the other hand, I wasn't involved in designing the Champion I/top 50 fix and thereby had the disadvantages of a modified ELO repeatedly beaten into my skull. If had been involved, I certainly would have looked at where I wasn't implementing the fix to see if it was causing problems there (it's just what good systems engineers do as a matter of course).

So let's look at the ELO modifications in the same way that we analyzed the Best General argument above. It is extremely obvious (and acknowledged) that rankings almost constantly rise in Splinterlands. Indeed, as mentioned above, the Splinterlands ELO modifications increases all rankings so radically that player's ranks need to be automatically dropped 25% or more at the end of each 15-day season. Now, I must acknowledge that always advancing is positive reinforcement which could be desired -- but I would also argue that it actually quickly turns hollow. The real goal is reaching higher levels as your skill improves, not mindlessly advancing because you've played more games (and then regularly being set back so that you can advance again).
Standard ELO does NOT increase the score of the winner by more than it decreases the score of the loser. Thus, the average ranking of all players doesn't constantly increase with the number of games played. And, most importantly, bots (and poor players) can't reach ridiculous levels because "a rising tide lifts all boats"
Before Splinterlands implemented its Champion I fixes, there were many more bots in the top 50 due to the fact that increased rankings were guaranteed by a greater number of wins. If the bot wasn't advancing, it was driving up the rankings of its competitors until it could advance. And this was entirely despite the fact that the bot's win percentage was 100% consistently significantly below that of comparably ranked players (or, statistically, there was far more covariance between number of games and ranking than there should have been). A good simple graph would have made this obvious (and even told you how many games a player had to play for a given win percentage to get to a desired ranking). And, I'll certainly commend the Splinterlands for recognizing and applying the correct fix.
Now, it must be noted that the bot flood problem wasn't quite as obvious at this point -- but it had been noticed. Why the team didn't immediately recognize that globally applying the ELO modification removal would have fixed that problem as well is beyond me. There is also the fact that recently solving a problem with a similar cause should have brought the same fix to mind when the bot flood problem did become urgent.

So, once the source of the problem is clear, we stand a chance of finding a good solution rather than a kludge. The obvious solution is to just remove the ELO modifications globally. This does, however, have side effects which do dramatically alter the ranking tempo of the game (the previously mentioned cycle of always advancing and then being dropped) in a way that may not be desired (but which I believe to be beneficial rather than detrimental).
But there is actually a second factor causing the problem whose solution causes much fewer such visible effects. The problem really isn't that rankings as constantly rising within seasons but that they are rising across seasons as well (until you hit the unmodified ELO wall at Champion I). If the real problem is that the cross-season average ranking is constantly rising, can't it just be fixed by ensuring that the seasonal reset always returns it to the same desired base level? At the end of the season, it would be trivial to calculate the average ranking and reduce everyone by the same factor necessary to return the average ranking to its desired value.
Both of these solutions have their relative pros and cons (the latter of which can frequently be prevented or ameliorated). If Splinterlands reverts to a straight ELO, ratings wouldn't have to be reset at the end of each season -- but then seasonal rewards would need to be made contingent upon a player playing at least a certain number of games). As an untried solution, relying solely on changing the seasonal reset may not be enough to completely solve the problem.
Fortunately, there is another incredibly minor set of changes that would be an improvement to both solutions and would be great preparation for when there are many more players in Splinterlands. Splinterlands already calculates and displays the exact position/placement of every player in the top 100. Why not do that for everyone? You could even base league and tournaments on Top X or Top X% rather than set rankings. This would easily allow all sorts of other simple adjustments as Splinterlands grows.
So . . . what am I missing this time? Are there any other concerns left? Or should we all speak up and try to get the Splinterlands team to reverse course? Please respond in the comments below.

Certainly has a lot to do with it at least.
Real true ELO is harsh and can be painful to many users... i think they tried to soften it's blow WHILE making up for not having real leagues. Which led to their bastardized system of elo that created a new set of problems some of which you described
I'm not sure most users are willing to see real ELO be used and ready to see their scores drop as much as they could. But hopefully after there are real leagues we try it.
Oh and so far I'm still a fan of collection scores but it really needs the real leagues thing so i think this in between time is gonna be a bit uncomfortable.
Yeah. I'm not sure how you soften the blow without opening the door for inflation.
But what about the second solution. All that is really needed is a minor adjustment to the end of season reset . . . .
Did I err in making ELO the first solution so no one pays attention to the second?
ELO has been tried, tested and rings true for many years now, so it's always a viable solution, regardless of the format of a ranking system. The only problem that ELO has is that it needs many players involved in order to self-correct as designed. Making an ELO ranking system within a game with (apparently) a big number of bots involved is problematic, as it will highlight the real players' skills more than what they are in reality (assuming the bots are bots and play sub-optimal in comparison with real people in games that have a randomness element to them).
My 2 cents on the apparent discussion.
Yes, too many bad bots will push not-bad players a bit higher -- but that isn't a huge problem unless the ranking system also has an upward trend.
Also, yes, the bots are bots -- but some of them are programmed well enough that they are legitimately in the top 50 (even though there is also an obnoxiously huge number that play terribly and have only first level decks to boot -- which don't require much skill anyways).
The reason why a pure ELO would be problematic for Splinterlands is because a game of Splinterlands is not pure skill. Card collections (the pay to win component) is important and there is also a heavy dose of randomness.
If Splinterlands was a game where everyone had access to the same cards. And then once both players submitted a team, the computer did one million simulations to decide who which team would win on average. In that scenario, then I agree a pure ELO system would make sense.
But there are lots of cases where the winner of a game is 50/50. And situations where one player chose the much stronger team but due to bad luck (like lots of misses), they end of losing. Chess doesn't have to deal with such scenarios.
Your arguments don't support your thesis - they are entirely disjoint and orthogonal except for the fact that ELO is best known for pure skill games. Yes, Splinterlands has luck as well as skill. But why does that make straight ELO bad? Same question about unequal card pools? And how do the two modifications that the team slapped on top of ELO compensate for whatever was bad about ELO?
And what about the second suggestion? All that is really needed is a minor adjustment to the end of season reset . . . .
Did I err in making ELO the first solution so no one pays attention to the second?