
[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Graphs 2.
As always, I highly suggest checking out the previous part before this one...
So, without further ado, let's get straight into it!
Graph Representation
There are two main ways of representing graphs:
- adjacency matrix
- adjacency lists
Let's get into each one separately...
Adjacency Matrix
If G is a graph with n vertices, then the adjacency matrix is an n x n matrix A, where each element aij is defined as:
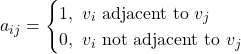
As such if there's an edge between vertices vi and vj there will be a 1 in the corresponding row-column pair of the matrix. Similarly, when there's no edge there will be a 0.
In the case of a directed graph the number of 1's equals the number of edges.
For multigraphs the 1 is replaced by the number of edges between the respective vertices.
Adjacency Lists
If G is a graph with n vertices then the corresponding n adjacency lists, one for each vertex, contain the vertices each vertex is adjacent to.
Such a representation can be used for both directed and undirected graphs, but not for multigraphs.
Example
Let's consider the following directed graph:
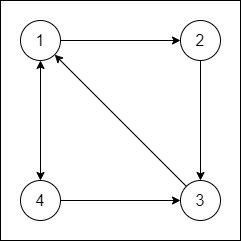
The corresponding adjacency matrix is:
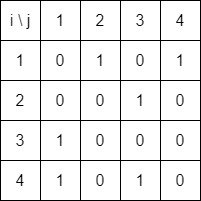
whilst the respective adjacency lists are:
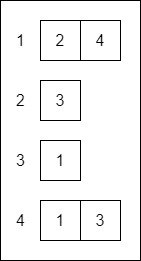
Graph Types and Properties
In addition to the types and properties mentioned last time, there are even more which are worth mentioning.
Isomorphic Graphs
Graphs are isomorphic if they are the same. Isomorphism is thus the analogy of equality in the context of graphs.
Of course, due to their nature it's possible to visualize graphs in various ways, different names in the vertices etc. So, graphs are basically isomorphic when it's possible to relate all edges 1-to-1.
For graphs G1 and G2 an isomorphism is basically a bijection f between the respective vertex sets V1 and V2, such that when (a, b) is an edge in G1 if and only if (f(a), f(b)) is an edge in G2.
For example the following graphs are isomorphic:
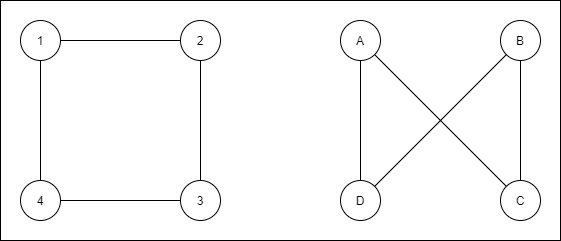
because vertices B and C are basically 3 and 2 respectively.
Subgraphs
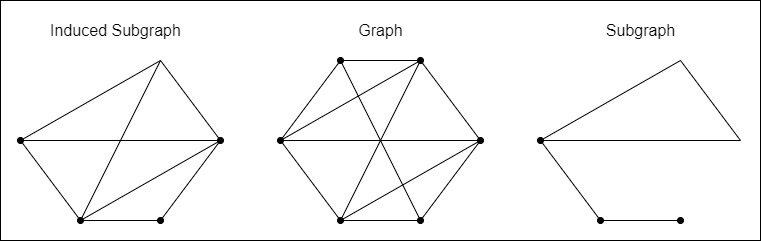
A subgraph of a graph consists of a subset of the vertices and edges of the "parent" graph. Therefore, if G = (V, E) and G' = (V', E') is a subgraph then V' ⊆ V and E' ⊆ E.
One special case is the induced subgraph, where every edge of E whose vertices are still in V' is an edge in E'. So, in order to create an induced subgraph some vertices and only their adjacent edges are removed.
Lastly, when removing only edges but keeping the original vertices of G, then the subgraph is a so called spanning subgraph.
For example:
Bipartite Graphs
A graph G whose vertices can be partitioned into two subsets V1 and V2, so that each edge connects a vertex from V1 to a vertex of V2 is known as a bipartite graph.
For example:
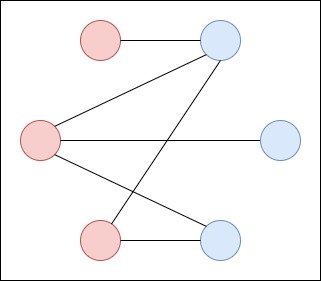
If each vertex of V1 is connected with an edge to each vertex of V2 then the graph is a complete bipartite graph.
Regular Graphs
A graph G is regular or more specifically K-regular if all vertices have the same degree K.
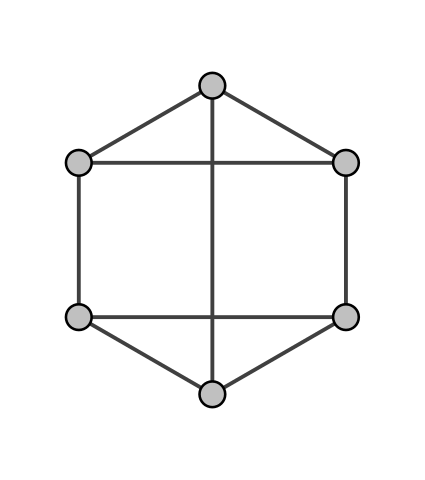
[Image 2]
Planar Graphs
Graphs that can be "drawn" on a flat plane with no edges crossing are called planar graphs.
For such graphs it's possible to define the concept of faces, where faces are basically the regions bound by edges and containing no edges on the interior.
Such graphs, also satisfy Euler's Formula:
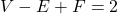
where V is the number of vertices, F the number of faces and E the number of edges.
For example:

[Image 3]
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
Images
- https://commons.wikimedia.org/wiki/File:Graph_example_(Graph_theory).png
- https://commons.wikimedia.org/wiki/File:3-regular_graph.svg
- https://commons.wikimedia.org/wiki/File:Point_location1.png
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
- Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
- Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
- Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
- Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
- Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
- Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
- Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
- Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
- Sequences and Recurrence Relations → Sequences (Terms, Definition, Arithmetic, Geometric), Recurrence Relations
- Probability → Probability Theory, Probability, Theorems, Example
- Conditional Probability → Conditional Probability, Law of Total Probability, Bayes' Theorem, Full-On Example
- Graphs → Graph Theory, Graphs (Vertices, Types, Handshake Lemma)
Final words | Next up
And this is actually it for today's post!
Next time we will continue on with Paths and Circuits...
See ya!

Keep on drifting!
Posted with STEMGeeks
Great Post!
!1UP
Would you please tell me how to post on stemgeeks and how to join community. We have any application where we can post and it'll upload on stemgeeks.
The frontend website for Stemgeeks is: https://stemgeeks.net/
You have received a 1UP from @luizeba!
@stem-curatorAnd they will bring !PIZZA 🍕
Learn more about our delegation service to earn daily rewards. Join the family on Discord.