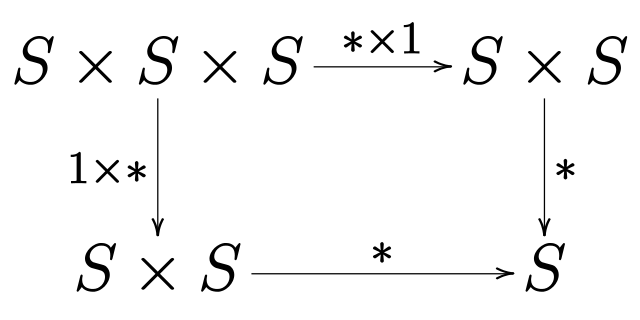
[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Group-like Structures. This is part 2, you can find part 1 here.
So, without further ado, let's get straight into it!
Magma
Easing the requirements of the definition of groups to the point that only the closure property has to be satisfied, yields an algebraic structure known as a Magma. A magma is thus a non-empty set together with a binary operation that satisfies closure (basically any function).
A magma clearly has way to few properties (only one), so let's add one additional property to come up with other structures...
Associative Magma (or Semigroup)
A magma that also satisfies associativity is basically a semigroup.
Unital Magma
A magma that satisfies identity is called an Unital magma.
Quasigroup
A magma which satisfies invertibility (or division), which basically means that division is always possible between any pair of elements is called a Quasigroup. A quasigroup doesn't have to be associative, nor does it have to include an identity element.
Loop
Adding an identity element to a Quasigroup yields a structure known as a Loop, which satisfies closure, identity and division.
Groupoid
A groupoid is commonly defined as a structure that doesn't satisfy closure but satisfies all other properties of a group (associativity, identity and invertibility). A groupoid basically easies the requirement of the binary operation, so that it doesn't have to be defined for all elements in the set.
Semigroupoid
A semigroupoid is a structure that satisfies only associativity.
Small category
A small category is a structure that satisfies associativity and has an identity element.
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- https://mathworld.wolfram.com/Group.html
- https://en.wikipedia.org/wiki/Group_(mathematics)
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
- Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
- Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
- Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
- Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
- Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
- Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
- Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
- Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
- Sequences and Recurrence Relations → Sequences (Terms, Definition, Arithmetic, Geometric), Recurrence Relations
- Probability → Probability Theory, Probability, Theorems, Example
- Conditional Probability → Conditional Probability, Law of Total Probability, Bayes' Theorem, Full-On Example
- Graphs → Graph Theory, Graphs (Vertices, Types, Handshake Lemma)
- Graphs 2 → Graph Representation (Adjacency Matrix and Lists), Graph Types and Properties (Isomorphic, Subgraphs, Bipartite, Regular, Planar)
- Paths and Circuits → Paths, Circuits, Euler, Hamilton
- Trees → Trees (Rooted, General and Binary), Tree Traversal, Spanning Trees
- Common Graph Problems → Shortest Path Problem, Graph Connectivity, Travelling Salesman Problem, Minimum Spanning Tree, Maximum Network Flow, Graph Coloring
- Binary Operations → Binary Operations (n-ary, Table Representation), Properties
- Groups → Groups (Properties, Theorems, Finite and Infinite, Abelian, Cyclic, Product, Homo-, Iso- and Auto-morphism)
- Group-like Structures (part 1) → Subgroups, Semigroups, Monoids
Final words | Next up
And this is actually it for today's post!
Next time we will cover Rings...
See ya!

Keep on drifting!
Posted with STEMGeeks
Thanks for sharing your maths knowledge here on Hive! During COVID Lockdown, we all learned how important distance learning is, and content like yours helped everyone across the globe!
!1UP
You have received a 1UP from @luizeba!
@stem-curatorAnd they will bring !PIZZA 🍕
Learn more about our delegation service to earn daily rewards. Join the family on Discord.