[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Groups.
So, without further ado, let's get straight into it!
Groups
Groups are algebraic structures studied by the branch of mathematics known as Group Theory. A group (G, *) is defined as a non-empty set G of elements together with a binary operation (also called group operation) on that set, which satisfies the following 4 properties:
- Closure : x * y ∈ G for all x, y ∈ G.
- Associativity : (x * y) * z = x * (y * z) for all x, y, z ∈ G.
- Identity : for any x ∈ G there exists an identity element e ∈ G so that e * x = x * e = x.
- Inverse : For any x ∈ G there exists the inverse of x, y ∈ G so that x * y = e = y * x.
The first property is commonly implied by defining the binary operation as a function, and so the number of properties is often 3 instead of 4.
Group Theorems
The properties or features of groups yield additional theorems.
First of all, the identity element is unique. It's easy to prove this. Choosing e and e' to be two identities in G results in ae = a and ae' = a. And so e = e', and there is only one identity element.
In a similar manner, there is also only one inverse for each element, meaning that the inverses are unique. Additionally, the inverse of the inverse equals the original element.
Due to associativity and identity, the left and right cancellation laws are also satisfied. This allows for simplifications, where the same quantity is removed on both the left-hand side and right-hand side.
Finite and Infinite Groups
Groups can be finite and infinite. A group (G, *) is a finite group when G is a finite set. Similarly, a group is an infinite group when G is a infinite set. The set of integers together with the addition operation form a valid infinite group.
Group Order
For a finite group, the group order is the number of elements it consists of. This is commonly denoted by |G|.
For example, a group of order 1 consists only of the identity element e. This special group is known as a trivial group. Similarly, a group of order 3 consists of the identity element and two other elements.
Abelian Groups
Groups which also satisfy the commutativity property (a * b = b * a) are known as Abelian Groups.
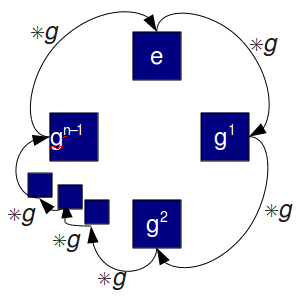
Cyclic Groups
Another common group type is the so called Cyclic Group. In such a group each element can be written in the form xn for some integer n and generator x.
Product of Groups
Groups can be multiplied in order to create more groups. This is commonly done through a direct product. For groups G and H it can be defined as:
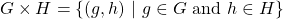
The corresponding group operation is:

Homomorphism
A group homomorphism is a mapping function f : G → H, which preserves the group operation, even when the binary operations of G and H are different. In other words, the identity property and group operation are still satisfied.
Isomorphism
For a homomorphism there might also exist the inverse mapping, known as a isomorphism. In such a case, the two groups are isomorphic and so basically the same.
Automorphism
Mapping from one group to another group where the set is the same but the binary operation is different, results in a mapping known as an automorphism.
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- https://brilliant.org/wiki/group-theory-introduction/
- https://mathworld.wolfram.com/Group.html
- https://en.wikipedia.org/wiki/Group_(mathematics)
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
- Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
- Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
- Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
- Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
- Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
- Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
- Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
- Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
- Sequences and Recurrence Relations → Sequences (Terms, Definition, Arithmetic, Geometric), Recurrence Relations
- Probability → Probability Theory, Probability, Theorems, Example
- Conditional Probability → Conditional Probability, Law of Total Probability, Bayes' Theorem, Full-On Example
- Graphs → Graph Theory, Graphs (Vertices, Types, Handshake Lemma)
- Graphs 2 → Graph Representation (Adjacency Matrix and Lists), Graph Types and Properties (Isomorphic, Subgraphs, Bipartite, Regular, Planar)
- Paths and Circuits → Paths, Circuits, Euler, Hamilton
- Trees → Trees (Rooted, General and Binary), Tree Traversal, Spanning Trees
- Common Graph Problems → Shortest Path Problem, Graph Connectivity, Travelling Salesman Problem, Minimum Spanning Tree, Maximum Network Flow, Graph Coloring
- Binary Operations → Binary Operations (n-ary, Table Representation), Properties
Final words | Next up
And this is actually it for today's post!
Next time we will continue on with more on Group Theory...
See ya!

Keep on drifting!
Posted with STEMGeeks