[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Paths and Circuits.
I highly suggest checking out the previous parts of the series before this one, or at least the previous two which are related to graphs...
So, without further ado, let's get straight into it!
Paths and Circuits
Starting off from a specific vertex of a graph it's possible to move along the edges. The series of edges that is traced or sequence of respective adjacent vertices is known as a walk. Discussing this topic of course only makes sense in the context of connected graphs.
There are various special types of paths that can be traced during a walk:
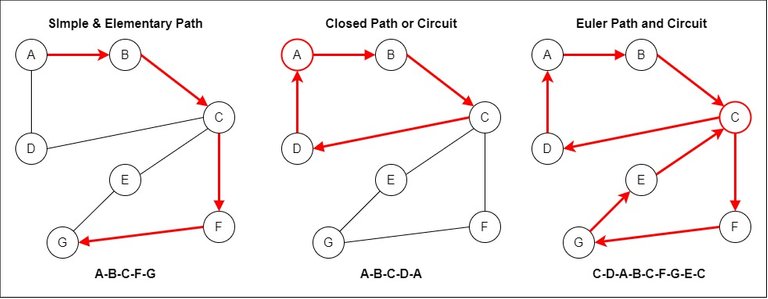
- Simple Path : no edge is repeated
- Elementary Path : no vertex is repeated
- Circuit or Closed Path : start and end at the same vertex
- Euler path : every edge exactly once
- Euler circuit : Euler path that starts and ends at the same vertex
- Hamilton path : every vertex exactly once
- Hamiltonian circuit : Hamilton path that starts and ends at the same vertex
For example, consider the following graph:
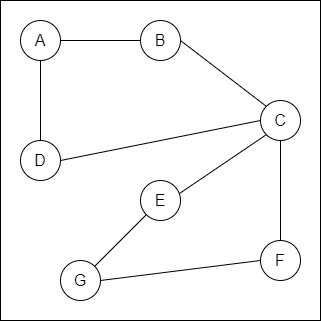
Some valid paths are the following:
Euler Paths and Circuits
In the case of the Euler paths and circuits it's easy to check if there's one:
A graph has an Euler circuit when all vertices are of even degree.
A graph has an Euler path when at most two vertices are of odd degree.
Let's not forget to mention that graphs with Euler (or Eulerian) paths are known as Euler (or Eulerian) graphs.
Hamiltonian Paths and Circuits
In the case of Hamiltonian paths and circuits there are no such rules. The problem is even difficult for computers to solve as it is considered NP-complete...
For example, a valid Hamiltonian Path is the following:
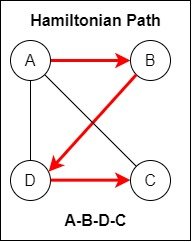
Of course, this graph has more Hamiltonian paths and circuits...
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
- Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
- Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
- Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
- Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
- Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
- Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
- Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
- Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
- Sequences and Recurrence Relations → Sequences (Terms, Definition, Arithmetic, Geometric), Recurrence Relations
- Probability → Probability Theory, Probability, Theorems, Example
- Conditional Probability → Conditional Probability, Law of Total Probability, Bayes' Theorem, Full-On Example
- Graphs → Graph Theory, Graphs (Vertices, Types, Handshake Lemma)
- Graphs 2 → Graph Representation (Adjacency Matrix and Lists), Graph Types and Properties (Isomorphic, Subgraphs, Bipartite, Regular, Planar)
Final words | Next up
And this is actually it for today's post!
Next time we will continue on with Trees...
See ya!

Keep on drifting!
Posted with STEMGeeks
Great Post!
!1UP
You're doing a really good job. Your posts inspire me😊