[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Trees.
So, without further ado, let's get straight into it!
Trees
Approaching graphs is easier when focusing on specific types of them. In the previous parts various types of graphs were discussed, but of course there are even more.
One such type are the so called trees. Trees are basically acyclic connected graphs, which means that they are connected graphs containing no cycles. If the graph is not connected then it can be a forest (multiple trees). A forest is basically an acyclic graph. Of course any connected forest is a tree.
Trees are useful in many applications as they satisfy the following properties:
- There is only one path between each pair of vertices
- The number of edges is one less than the number of vertices (e = v - 1)
Rooted Trees
Trees don't have any clear order as is, but it's common to specify a root vertex with only outgoing edges. Such trees are known as Rooted Trees.
In the context of rooted trees, vertices are given special names. When two vertices are adjacent then one of them is known as the parent and the other as the child of the parent. The one closer to the root is the parent. That way, all non-root vertices will have exactly one parent. Vertices with the same parent are siblings.
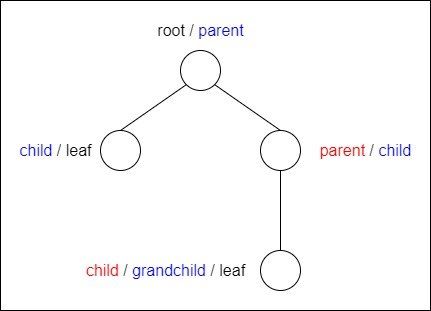
This logic extends further, meaning that the child of a child vertex is a grandchild etc. In general, vertices with a path to an ancestor vertex are its descendants. So, all vertices of a tree are descendants of the root. Last but not least, vertices with no children are known as leaves.
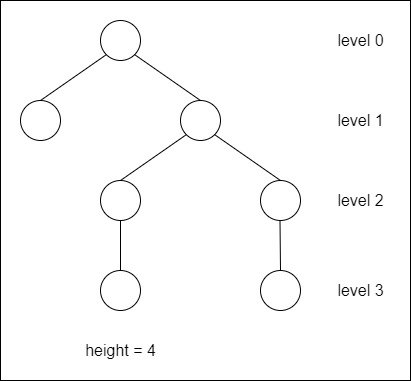
The vertices of a tree also have levels. The root has a level of zero. The children of the root have a level of one. This logic extends, meaning that each child has a level more than its parent.
The maximum number of vertices in a branch is known as the depth or height of a tree. The depth of the root vertex is defined as one, and so the depth is greater then the maximum level of the tree.
General and Binary Trees
General trees can have any number of children. On the other hand, in binary trees each vertex can only have up to 2 children. This limitation makes such trees very useful in lots of computer science applications.
A binary tree can always be split into two subtrees: the left subtree and the right subtree, which have the left child (and right child respectively) of some vertex as a root.
Tree Traversal
Binary Trees can be traversed using three methods:
- pre-order traversal
- post-order traversal
- in-order traversal
All of these are recursive processes. The main difference is when the root / parent is visited. In pre-order the root / parent is visited first, and then the left subtree, right subtree respectively. In post-order, the root is visited last. Finally, in in-order, the root is visited in between, yielding a left -> root -> right order.
Spanning Trees
Many algorithms can be written for trees because of the simple traversal mechanisms. In order to be able to use them in the case of any connected graph as well, a subgraph known as a spanning tree is taken from the graph, which contains all the vertices of the original graph but is a valid tree. Every connected graph has a spanning tree, and mostly multiple such trees. Finding the minimum spanning tree is a very common problem in Graph Theory and Computer Science.
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
- Set Operations → Venn Diagrams, Set Operations, Properties and Laws
- Sets and Relations → Cartesian Product of Sets, Relation and Function Terminology (Domain, Co-Domain and Range, Types and Properties)
- Relation Closures → Relation Closures (Reflexive, Symmetric, Transitive), Full-On Example
- Equivalence Relations → Equivalence Relations (Properties, Equivalent Elements, Equivalence Classes, Partitions)
- Partial Order Relations and Sets → Partial Order Relations, POSET (Elements, Max-Min, Upper-Lower Bounds), Hasse Diagrams, Total Order Relations, Lattices
- Combinatorial Principles → Combinatorics, Basic Counting Principles (Additive, Multiplicative), Inclusion-Exclusion Principle (PIE)
- Combinations and Permutations → Factorial, Binomial Coefficient, Combination and Permutation (with / out repetition)
- Combinatorics Topics → Pigeonhole Principle, Pascal's Triangle and Binomial Theorem, Counting Derangements
- Propositions and Connectives → Propositional Logic, Propositions, Connectives (∧, ∨, →, ↔ and ¬)
- Implication and Equivalence Statements → Truth Tables, Implication, Equivalence, Propositional Algebra
- Proof Strategies (part 1) → Proofs, Direct Proof, Proof by Contrapositive, Proof by Contradiction
- Proof Strategies (part 2) → Proof by Cases, Proof by Counter-Example, Mathematical Induction
- Sequences and Recurrence Relations → Sequences (Terms, Definition, Arithmetic, Geometric), Recurrence Relations
- Probability → Probability Theory, Probability, Theorems, Example
- Conditional Probability → Conditional Probability, Law of Total Probability, Bayes' Theorem, Full-On Example
- Graphs → Graph Theory, Graphs (Vertices, Types, Handshake Lemma)
- Graphs 2 → Graph Representation (Adjacency Matrix and Lists), Graph Types and Properties (Isomorphic, Subgraphs, Bipartite, Regular, Planar)
- Paths and Circuits → Paths, Circuits, Euler, Hamilton
Final words | Next up
And this is actually it for today's post!
Only a few more parts and the series is officially over...
See ya!

Keep on drifting!
Posted with STEMGeeks