
Introduction
Hey it's a me again @drifter1!
First of all, I'm very sorry for the loooong break. I had to do a lot in my Master' thesis and was also promoted at the job I'm doing in parallel with my studies. My current + new objective in Hive/PeakD is one post per week as I will also start my PhD quite soon. I have a very long TO-DO list but I am open to ideas from YOU all as well.
Today we continue with Mathematics, and more specifically the "Number Theory" series, in order to get into Diophantine Equations as promised back in October 2022. As usual we will first get into theory and then into practice.
So, without further ado, let's get straight into it!
Diophantine Equations
A Diophantine equation is any polynomial equation with two or more integer unknowns which have integer coefficients, as shown below.

Linear Diophantine Equations
When the integer unknowns each have at most a degree of 1 (no powers of 2, 3 etc.) then the Diophantine equation is called linear.
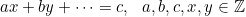
Homogeneous Linear Diophantine Equations
When the Diophantine equation has (0, 0, ...) as a solution, then the Diophantine equation is called homogeneous.
Below is the general specification of a homogeneous linear Diophantine equation.

Linear Diophantine Equation with 2 Unknown Integers
A linear Diophantine equation with 2 unknown integers is defined as follows:
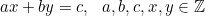
Criterion of the Existence of a Solution
When c = 0 then the linear Diophantine equation is homogeneous and as such x0 = 0, y0 = 0 is a solution.
Therefore, a homogeneous Diophantine equation always has a solution.
If c ≠ 0 then a solution exists only when the GCD of a and b divides c.
When the condition "GCD(a, b) | c" isn't true then there are no solutions for the linear Diophantine equation.
Set of Solutions
In the case of a homogeneous linear Diophantine equation (c = 0) the set of solutions is as follows:
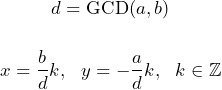
For a linear Diophantine equation with c ≠ 0, when the GCD of a and b, d = GCD(a, b), has been determined and when it divides c the solutions are found by determining the solution x0, y0 for the following Diophantine equation:

One solution for the original Diophantine equation is thus:

The general solutions for the original linear Diophantine equation can be proven (by substitution) to be of the form:

Example
Find the solutions (if any) for the following linear Diophantine equation:

Solution
Using prime factorization the coefficients can be represented as follows:
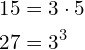
The common prime factor is 3 and as such the GCD is:
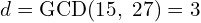
Let's determine a solution of the following linear Diophantine equation:
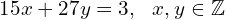
A solution is x = 2, y = -1, therefore a solution for the original Diophantine equation is the following:

The general solutions are therefore of the form:

Exercise
Does the linear Diophantine equation from the example have any positive solution(s)?
RESOURCES:
References
- https://brilliant.org/wiki/number-theory
- https://math.libretexts.org/Courses/Mount_Royal_University/MATH_2150%3A_Higher_Arithmetic/5%3A_Diophantine_Equations
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Number Theory, Why Number Theory, Series Outline
- Divisibility → Divisibility, Divisibility Rules
- Factorization and Euclidean Algorithm → Factorization, Euclidean Algorithm and GCD, Division Algorithm using Calculator
- Prime Numbers → Prime, Composite and Co-Prime Numbers, Prime Test (Sieve of Eratosthenes)
- Divisibility Examples → Divisibility Properties, Examples (Proof through Mathematical Induction, Properties, Solving Subproblems)
- GCD and LCM → Greatest Common Divisor (GCD), Euclidean Algorithm and Prime Factorization calculation methods for GCD, Least Common Multiple (LCM), Brute Force, Prime Factorization Method and GCD calculation methods for LCM
Final words | Next up
And this is the end of today's post!
Not sure what the next post on Number Theory will be about.
See ya!

Keep on drifting!
Exercise Solution
Let's determine for which m the x and y equations >= 0:
The only integer value for m is 4, therefore the only positive solution is (4, 0) as shown below: