In this article, I’ll cover various topics related to bonds and the maths behind them. Also, the implementation of them in Python.
Content:
- Zero-Coupon Bond.
- Yield to Maturity (YTM).
- Price of Bond.
- Bond Duration.
- Bond Convexity.
Zero-Coupon Bond:
- A Zero Coupon bond is a debt instrument, that trades at a discount of its face value.
- The difference between the Purchase price & Face value of a bond, Indicates the investor's return.
Zero-Coupon Bond Formula:
Image Courtesy: https://www.wallstreetmojo.com/zero-coupon-bond/
Zero-Coupon Python Code:
The amount of 96.11 invested for 2 years compounded annually @ **2% interest **will return **100 **at maturity.
Yield to Maturity (YTM):
- YTM is the total return one can expect when all coupons and principal are received and bonds held till maturity.
- YTM is basically the internal rate of return (IRR) if held till maturity.
- With the help of the Scipy optimization function in python, we can solve for YTM to get desired output.
Yield to Maturity (YTM) (Formula):
Image Courtesy: https://theintactone.com/2019/05/18/saim-u1-topic-9-yield-to-maturity/
Yield to Maturity (YTM) (Python Code):
YTM of bond is 9.37%. if the **bond price **is currently **95.0428 and the **face value of the bond is 100, maturity is 1.5 years with 5.75% coupon payment semi-annually.
Price of Bond:
- Bond price is the present discounted value of the future cash stream generated by a bond.
- When we know YTM we can plugin and get the value of the bond.
Price of Bond (Python Code):
Bond Duration:
- Duration measures a bond's price sensitivity to changes in interest rate.
- Modified duration measures the price change in a bond given a 1% change in interest rate.
- The modified duration of a bond can be thought of as the first derivative of the relationship between price and yield.
Bond Duration Formula:
Image Courtesy: Wikipedia.
Bond Duration Python Code:
In the above scenario, the modified duration is 1.39 years.
Bond Convexity:
- Convexity is the sensitivity measure of the duration of a bond to yield changes.
- Convexity is the second derivative of the relationship between the price and yield.
Bond Convexity (Formula):
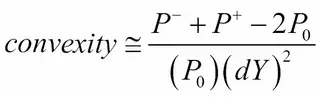
Bond Convexity (Python Formula):
I hope I have covered topics with relatively easy to understand and it'll be useful to others to implement in python.
You can access the full python code on the GitHub page mentioned below.
https://github.com/abhaydd22/BondMaths/blob/main/BondMaths.ipynb
Thanks