In the last article, we saw how to set-up a coarse-grained simulation using LAMMPS software. In today's article, I will discuss how to come up with a model to simulate a coarse-grained lipid system. In particular, we will see an example model[1] from a 2003 paper by Dr. Oded Farago. The reason why I am using this model is because of its simplicity.
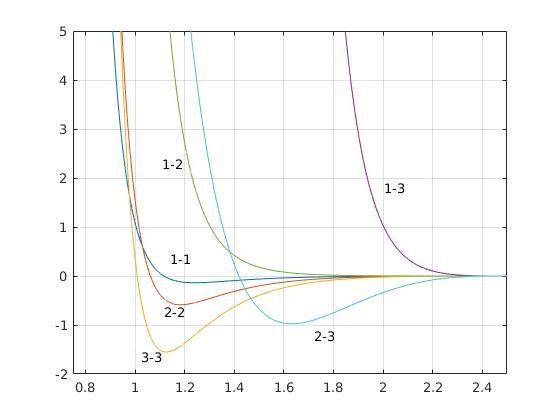
(Farago Potentials for 3 particle lipid. See below for details)
Points to be careful before modelling this system
Lipid systems like vesicles or bilayer sheet membranes are always in an environment of solvent(water). The water outside and inside of lipid bilayer sheet also acts a force on it such that the bilayer maintains the structure without losing individual lipids from it. Then, Why do we want a solvent-free lipid model? First of all let us address this question. In all-atom molecular dynamics systems where we have explicit water molecules, most of the computing power is spent to simulate them. The total water particles is so huge compared to lipids/protein atoms in that system. So although the focus of study is protein or lipid system, we spent most of the time and computing power to simulate these water molecules. That is the reason why we are compelled to remove explicit water molecules, especially in a scenario where you have lesser computing power and if you want to study the system in longer length and time scales. But when you dont account for water, you will have to account the effect of this solvent-lipid interaction via the effective potential(force-field) you are going to come up with. We will describe such a model today.
An example Model
The example model which I am going to explain is Farago model[1]. The original paper was a MC(monte-carlo) simulation work.(I will use this model to implement MD simulations which is technically possible.) The lipid is modelled via a three particle rigid trimer.
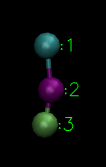
(particle 1: hydrophilic HEAD, particle 2: hydrophobic TAIL1 and particle 3: hydrophobic TAIL2)
Instead of going into the equations of the potentials let us visually inspect the potentials. I have given the parameters in the table below. But looking at the graph will help understand the potentials better. All the potentials are smoothed using the Taylor series terms upto second derivative terms so that both the potential and force smoothly tend to zero at the cut-off value 2.5 \sigma. We have already mentioned about cut-off value previously. This is the distance till which LJ interactions are calculated when considering interaction between i and j particles. Now let us inspect the potentials. The main points to note are:
- The model should let the lipids diffuse laterally and transversally(flip-flops)
- The effect of solvent should be taken care of so that lipids dont escape the bilayer. But the attraction should be very strong such that this interaction hampers lateral diffusion.
- The model should reproduce different phases like gel phase and fluid phase
The author has decided to choose the parameters on a trial and error basis which accounts for the absence of solvent via making the interaction between hydrophobic beads stronger to the point where the stability of the membrane is preserved and the lateral diffusion is taken care of.
Parameters in Farago model:
| Interaction(b/w i and j atoms) | \epsilon_ij (kT) | \sigma_ij |
|---|---|---|
| 1-1 (12-6 LJ potential ) | 0.1875 | 1.1 |
| 2-2 (12-6 LJ potential ) | 0.75 | 1.05 |
| 3-3 (12-6 LJ potential ) | 1.875 | 1.00 |
| 2-3 (unconventional 2-1 LJ potential ) | 375 | 0.525 |
| 1-2 (12 powered LJ repulsion) | 1.1375 | 1.15 |
| 1-3 (18 powered LJ repulsion) | 200 | 1.4 |

(These are the potentials between i-th and j-th type particles represeneted as 1-1, 1-2 etc according to the Farago model. The x-axis is distance r in units of \sigma and y axis is the potential in units of kT. Picture courtesy: @dexterdev, adapted from [1])
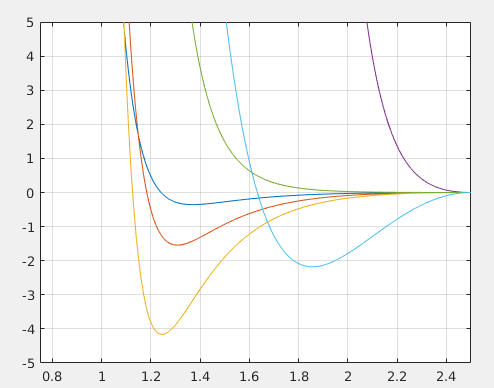
(Corresponding forces from the potentials. Picture courtesy: @dexterdev)
Another important parameter which this model depends on is the projected area Ap. In the paper, a bilayer sheet system of 500 lipids on both leaflets is the example. In the lower projected area like Ap = 26.875^2, hexagonal order among lipids was observed and no diffusion was exhibited. Beyond these values of Ap(28.125^2) diffusion was observed and the membrane becomes fluid. The higher projected area(Ap=30^2 \sigma^2 units) for the same system of 500 lipids on both leaflets result in pores and flip-flops.
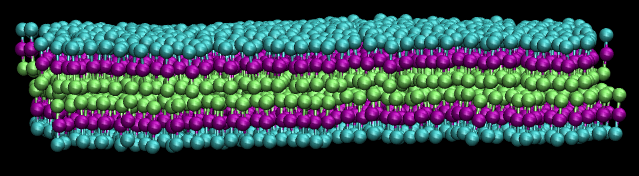
(side view of lipid bilayer sheet. PC: @dexterdev)

(top view of lipid bilayer sheet. PC: @dexterdev)
Shortcomings of the model
Although this is a very simple model, it is a very fine tuned one! This is one of the deficiency of the model. Fine tuned in the sense that it depends of many fixed parameters. So there are other models like Deserno model[2] which overcomes this disadvantage.
What next?
I intend to proceed with my molecular dynamics experiments using Farago model. Let us learn together. :) Hope you enjoyed the article. Tell me your comments and doubts here.
Bye for today!
I just noticed that some of the potentials are monotone and that some have a single sign change. Why does this difference exist between for example the 2-3 and 1-3?
good questions. In fact, I am very glad you asked me this. So think about our three particles in each lipid:
1is hydrophilic and2and3are hydrophobic particles. Like particles interacts strongly and will have a minima. 2-3 interaction(means 2 of one lipid and 3 of another near by lipid) should be also have an attractive term, since both are hydrophobic terms. Think about 1-2 and 1-3 interaction terms now: They should never attract each other. So they will have potentials which mimic repulsion only. No well for them and so they are monotone. Did this clarify your question?Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
Thanks for using the STEMsocial app and including @steemstem as a beneficiaryi, which give you stronger support.
Learn something new......Thanks for sharing.....Spread Knowledge......✌️ ✌️ 🤓 ✌️ ✌️
#posh