In simple harmonic motion, the displacement varies sinusoidally with time – and this is a lot more complicated than if displacement were linear with time. The figure below shows the displacement for an oscillator behaving sinusoidally with time.
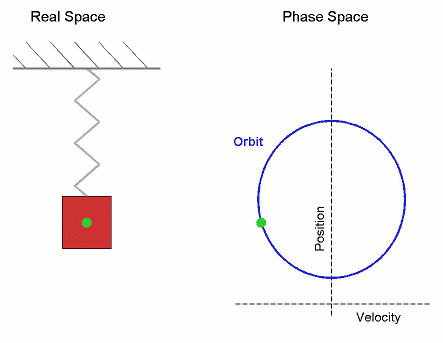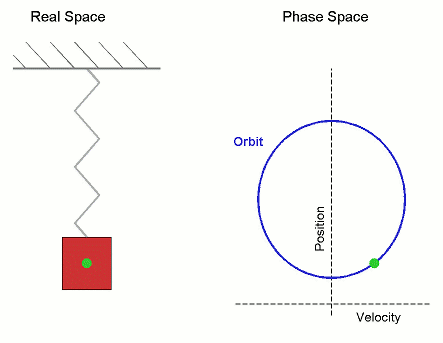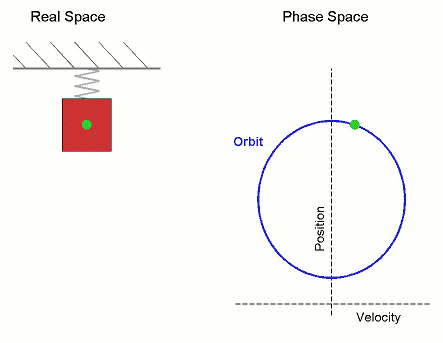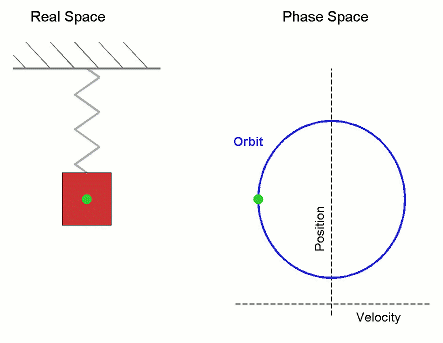
It is plotted with maximum displacement at time t = 0 so that x = A cos ωt = A. The velocity of the oscillator at any time is given by the small change in displacement Δx which occurs during a small change in time Δt. That is:
Velocity = Δx/Δt
This velocity is the gradient at any point on the displacement-time curve in the figure shown. We can see the following:
- At t = 0, the gradient is zero.
- At t = T/4, the gradient is negative and is the maximum possible negative value.
- At t = T/2, the gradient is again zero.
- At t = 3T/4, the gradient has the maximum possible positive value.
- At t = T, the oscillator has returned to its starting position and the gradient of the curve is zero.
We can plot the complete range of values of the gradient. This gives us the velocity-time curve shown. We see that the shape of the curve is similar to that of the first figure but is displaced along the time axis. The velocity is zero at time t = 0. It is in fact given by sin wt; and since the velocity starts off in a negative direction, the dependence is -sinωt. The velocity lags the displacement by π/2. We say that it is out of phase by - π/2.
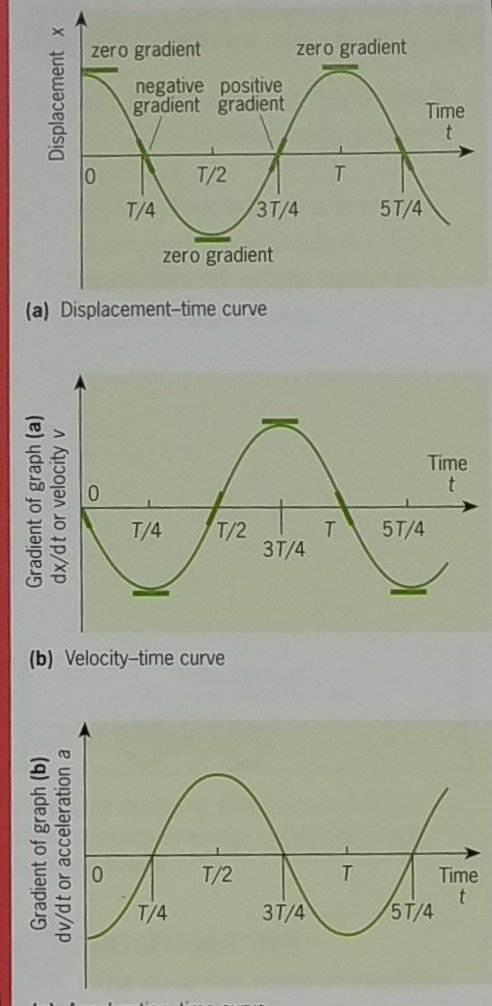
Now we take the velocity-time curve and consider the gradient Δv/Δt in a similar way. This gives us the variation of acceleration with time. We see that acceleration is in opposite phase to the displacement that is, they are out of phase by π, so that when one is at a maximum positive value the other is at a maximum negative value, and so on. Acceleration can be represented by -cos ωt.
Proof by calculus
The relationships for velocity and acceleration can also be shown by calculus.
Displacement is given by:
x = A cos ωt
To find the velocity, v, we differentiate:
v = dx/dt = d/dt(A cos ωt)
= -Aω sin ωt
We differentiate again to find the acceleration, a:
a = dv/dt = d/dt(-Aω sin ωt)
-Aω2 cos ωt
But we can replace A cos ωt by x.
So:
a = -w2x
The physics of the curves
Do the curves of the figures make sense? We can see that the velocity is maximum at zero displacement. Think of a pendulum. It swings fastest at the centre of its swing. What about the trolley connected to the two springs? It is also moving fastest at its central position. On the other hand, in both examples, velocity is zero at maximum displacement. The pendulum and the trolley are at rest for an instant as they reverse direction of movement. But the force is a maximum here and the acceleration must be a maximum. The force is returning the pendulum or the trolley back to its central equilibrium position and so the acceleration must be negative compared with displacement. In the central position, there is no horizontal force on the pendulum. In the case of the trolley, the horizontal forces exerted by the springs exactly balance out.
So what is simple harmonic motion?
Simple harmonic motion (s.h.m.) is motion in which the acceleration is directly proportional to the displacement from a fixed point and is directed towards this point. We can see, both from the graphical treatment and from the calculus above, that displacement varies sinusoidally with time and that acceleration is proportional to the displacement. Acceleration is oppositely directed, as shown by the negative sign.
To show that the motion of a pendulum is simple harmonic motion
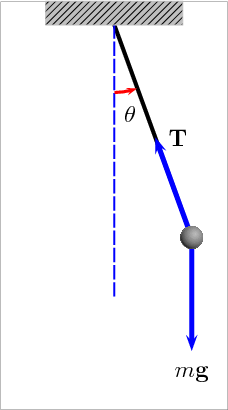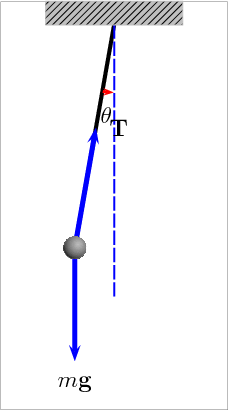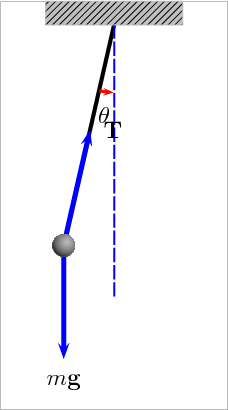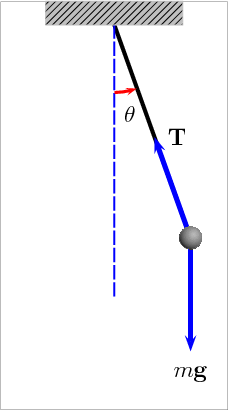
We need to show that the acceleration of the bob is proportional to its displacement from the centre of motion, which is taken as the vertical position. Suppose we have a bob of mass m. A gravitational force mg will act on the bob vertically downwards. There is also a tension T acting in the string. When the bob is displaced from the vertical by an angle θ, the tension acts on the bob at an angle θ to the vertical. We resolve forces along and perpendicular to the string. Along the string we have:
T = mg cos θ
The tension in the string must be equal and opposite to the gravitational force on the bob as resolved in the direction of the string.
Perpendicular to the string is an unbalanced force of mg sin θ. This force acting on the bob of mass m must give it an acceleration a in the direction of decreasing θ (that is, it acts in the opposite direction to the displacement).
From this we can say that:
mg sin θ = -ma
Or:
g sin θ = -a
If θ is very small and measured in radians, then sin θ = 0 and we get:
gθ = -a
So we see that acceleration is proportional to the angular displacement θ.
Pendulums and springs
THE PERIOD OF A SIMPLE PENDULUM
Let x be the displacement of the bob from the vertical in a horizontal direction and l be the length of the pendulum. Then for small θ:
θ = x/l
We know from above that gθ = -a, so:
gx/l = -a…………………[1]
The acceleration is proportional to the displacement x, in line with the definition of s.h.m. We compare equation 1 with the equation a = -ω2x for s.h.m.:
So that:
ω2 = g/l
Since ω = 2πf: 4π2f2 = g/l
giving: f = 1/2π(√g/l)
The period of the pendulum is T = 1/f
so: T = 2π√(l/g)
Note that this expression is only true provided θ is small (less than approximately 10°, or less than 0.2 radians).
THE PERIOD OF OSCILLATION OF A MASS SUSPENDED FROM A SPRING
The force exerted by the spring is:
F = -kx
Where x is the extension or compression of the spring from its equilibrium length, and k is the spring constant. When a mass m is suspended from the spring, it will already be stretched through an extension x0, given by kx0 = mg.
After pulling the mass down a further distance x and letting go of the mass, as in the diagram, we have:
- A force downwards equal to mg due to the gravitational force on the mass,
- A force upwards equal to k(x + x0) due to the tension of the stretched spring.
These are not equal and so there is a net force acting on the suspended mass giving it an acceleration a. As force equals mass × acceleration, assuming that we give a downward force a plus sign and an upward force a minus sign, we have:
-k(x + x0) [force exerted by spring] + mg [force due to gravity]= ma [resulting net accelerating force]
As the upward force k(x + x0) of the spring is greater than the downward force on the mass mg, the acceleration is upwards and hence has a negative value. The equation continues to apply as the spring contracts through its equilibrium extension.
Now, by Hooke’s law we can replace mg by kx0 in the equation to give:
so: -k(x + x0) + kx0 = ma
-kx = ma
a = (k/m)x
Comparing this with the equation for s.h.m.:
a = -w2x
we obtain:
ω2 = k/m
This gives the period of oscillation for the suspended mass on the spring as:
T = 2π/ω = 2π√(m/k)
ENERGY CHANGES IN AN OSCILLATING SYSTEM
In all the examples of s.h.m. that we have considered – that is the pendulum, the mass on a spring and the vibrating dynamics trolley – the velocity v of the oscillating mass m varies in the same way. It goes from a maximum when it passes through the equilibrium position to zero at maximum displacement when the direction of motion is instantaneously changing.
For each system, the kinetic energy at any time is ½ mv2. We can now look at how this energy varies.
ENERGY-TIME CURVES
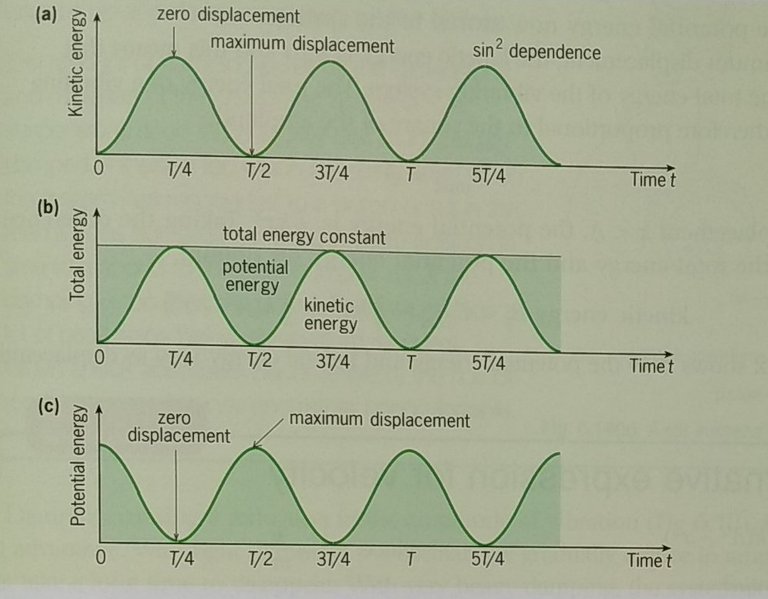
Since the velocity v changes sinusoidally with time as shown below, the variation of kinetic energy with time can be shown by squaring the velocity as in (a). The total energy of the oscillating system must remain constant. So, as the kinetic energy rises and falls, it is being transferred back and forth into another form of energy. This form must be potential energy. We can see this energy as the difference (shaded areas) between the constant level of energy and the kinetic energy as in the figure (b). Alternatively, potential energy can be plotted positively in the same way as kinetic energy, as in figure (c), and is seen to be out of phase with kinetic energy by a quarter of a period.
ENERGY-DISPLACEMENT CURVES
We can also show the variation of kinetic energy and potential energy with displacement x, rather than with time t, and this gives us curves of a different shape. When working out the form of these curves, it is easiest to start with the potential energy contribution to the energy.
As before, let’s consider a mass connected horizontally between two springs. (This is so that we do not need to consider gravitational potential energy.) We will take the force constant as k for the two springs acting on the mass. To move the trolley from its equilibrium position at x = 0 to displaced position x requires an applied force Fapplied given by:
Fapplied = kx
This applied force is equal and opposite to the restoring force exerted by the springs.
The work done is force × distance and is equal to the triangular area under the applied force plot.
Work done = ½ Fapplied xmax = ½ kxmax 2
But xmax is the maximum displacement or amplitude of vibration. I called this A earlier. So:
Work done = ½ kA2
This is the potential energy now stored in the springs.
At maximum displacement, the kinetic energy is zero and this means that ½ kA2 is the total energy of the vibrating system. The total energy of a vibrating system is therefore proportional to the square of the amplitude:
Etotal∞ A2
For a displacement x < A, the potential energy is ½ kx2. Taking the difference between the total energy and the potential energy we obtain:
Kinetic energy Ek = Etotal – ½ kx2 = ½ k(A2 – x2)
These formulas are enough and I will pause here for now. In the next post I will discuss damping and forced oscillations and resonance. I promise no more physical and mathematical expressions. Till then, I remain my humble self @emperorhassy.
Thanks for coming.
REFERENCES
https://www.khanacademy.org/science/ap-physics-1/simple-harmonic-motion-ap/introduction-to-simple-harmonic-motion-ap/a/introduction-to-simple-harmonic-motion-review
https://www.britannica.com/science/simple-harmonic-motion
https://en.wikipedia.org/wiki/Simple_harmonic_motion
https://www.toppr.com/ask/question/the-period-of-oscillation-of-a-mass-suspended-from-a-spring-is-2-second-along/
https://spark.iop.org/investigating-mass-spring-oscillator
https://courses.lumenlearning.com/boundless-physics/chapter/periodic-motion/
https://deutsch.physics.ucsc.edu/6A/book/harmonic/node11.html
https://courses.lumenlearning.com/physics/chapter/16-5-energy-and-the-simple-harmonic-oscillator/
https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_https://www.zigya.com/study/book?class=11&board=mbose&subject=Physics&book=Physics+Part+II&chapter=Oscillations&q_type=&q_topic=Simple+Harmonic+Motion&q_category=&question_id=PHEN11040388
https://www.khanacademy.org/science/ap-physics-1/simple-harmonic-motion-ap/energy-in-a-simple-harmonic-oscillator-ap/a/energy-of-simple-harmonic-oscillator-review-ap
https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.