RE: Citizen science: Simulation of a neutrino signal at CERN’s LHC with its uncertainties

[lemouth]

I'll need to show the error of the cross section (plotted in the figure) from value before it was truncated?

I didn't understand the above statement, and I therefore do not know how to answer the question. I am really sorry. What do you mean by "before it was truncated"? Do you mind providing some more details? Thanks in advance.

Comments

[travelingmercies]

Oh, sorry. Let me rephrase my question. From what I understand in your previous comment here:

I have the impression that you took the numerical error associated with the calculation (that is indicated in the first table) as the error to include in the plot. This error, which is of a few permiles, has however nothing to do with the one that originates from the truncation of the perturbative series. The latter is of the order of 10%.

..is that what I need to include in the plot is the truncation error of the cross section?

I re-plot the figure with the new error values got from the terminal log. Can you confirm if this one is right? Thank you. :)

[lemouth]

OK I think I got your point. Let me try to re-explain (if I am off, please let me know again), with the example of the 50 GeV mass point. I will also use approximate values for the errors, but this should not change the flow of the discussion.

The calculation has returned three types of errors, plus a central value.

• The central value is 3.843 fb, as shown in the first table.
• The associated purely numerical error is 0.00892 fb, as shown in the first table. This corresponds to a relative error of 0.2%. It comes from the fact that the calculation involves a highly-dimensional integral that is computed via a Monte Carlo method (we transform the integral into a sum over a given number of points, divided by the number of points). It can be made arbitrarily small by running the code longer (and including thus more points in the sum). We must check that this error is small enough (it is the case here) and negligible relative to all other errors (it is the case here). It can then be omitted.
• The scale uncertainties correspond to the truncation of the perturbative series that I mentioned in my blog. They have a well defined origin: our calculation only includes the first term of the perturbative series, and we need to estimate the impact of the missing terms. They are of about 2.5% (cf. second table).
• The PDF uncertainties correspond to the uncertainties inherent to our choice on how to link the colliding protons to their content. They are of about 5.8% (cf. second table).

The total error on the results is obtained by the combination of the PDF and scale uncertainties, and we get a total relative error of about 6.4% (cf. second table). This gives a corresponding error of about 0.25 fb, which needs to be reported as an error bar on the figure. I have the impression that your error bars (on the last figure) are too big.

Is all of this clearer?

Cheers!

[travelingmercies]

Oh, I totally understand it now! Thank you. :) I replot the figure (again haha) and got this:

[lemouth]

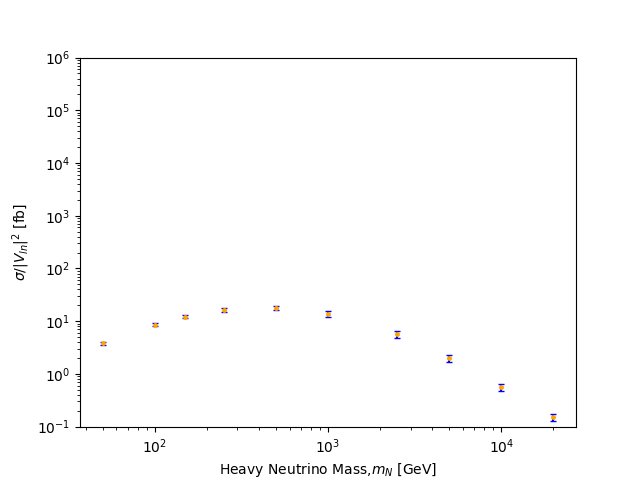
Excellent! Glad to see this (this looks OK).

Note that I will wait a bit before releasing a new episode, as some community members mentioned to me that they wanted to try the project out. Therefore, episode 7 should be released by the end of the month.

Cheers!

[travelingmercies]

Oh, nice! That's really great. Your mention of the project during HiveFest sparked curiosity, I noticed it from the the live chat during the broadcast. :)

[lemouth]

I have indeed done that, and I actually explicitly mentioned your work, as well as that of @agreste. I believe it was a fair thing to do.

For the rest, I still hope that @eniolw will catch up, so that we will have three up-to-date participants in the project, and that @itharagaian (and possibly others who mentioned it to me at HiveFest) will join us!

Cheers!

[itharagaian]

Gotta startup a specific machine, but as soon as I feel better, be sure I will join and try it out

!PGM
!PIZZA