¡Hola amigos de Hive Blog!
Reciban un cordial saludo.
La descripción y el comportamiento de un gran número de sistemas han sido posibles gracias al uso de herramientas matemáticas basadas en la transformación del dominio del tiempo al dominio de la frecuencia de las señales que gobiernan dichos sistemas.
Una de las trasformaciones de dominio con una gran variedad de aplicaciones es la transformada de Fourier.
La transformada de Fourier es ampliamente utilizada en distintas áreas de la física e ingeniería en el procesamiento e interpretación de señales con aplicaciones en la geofísica, las telecomunicaciones, sistemas de control, fenómenos ópticos, procesamiento de imágenes, etcétera.
En los análisis de redes, la transformada de Fourier además de simplificar y facilitar el análisis matemático, permite describir el comportamiento de parámetros como la amplitud, la fase y la densidad de potencia de una señal como una función de la frecuencia.
Dada su importancia, con el objeto de fortalecer nuestros conocimientos en el análisis de una red eléctrica, en este trabajo utilizaremos la transformada de Fourier para obtener respuesta en tiempo y en frecuencia de un circuito eléctrico.
Fundamentos teóricos
La transformada de Fourier es una generalización de la serie de Fourier aplicable a señales no periódicas.
A diferencia de las series de Fourier, cuyos espectros de frecuencia son de tipo discreto, la transformada de Fourier genera espectros continuos de frecuencia.
Para que una señal tenga transformada de Fourier se debe cumplir que la misma presente un número finito de discontinuidades en un intervalo de tiempo finito y sea totalmente integrable .
Matemáticamente esta condición puede expresarse de la forma:
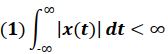
La transformada de Fourier esta definida por la siguiente ecuación:
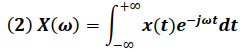
x(t) → Señal en tiempo
X(ω) → Señal en frecuencia (Espectro de x(t) )
Simbólicamente es expresada de la forma:
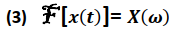
Usando la identidad de Euler en la expresión 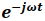 , se tiene:
, se tiene:
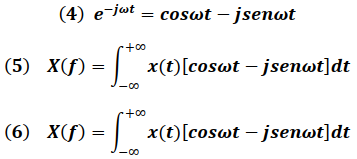
Para señales "x(t)" con simetría par o impar la ecuación (6) se escribe, según el caso, de la forma:
Para "x(t)" par
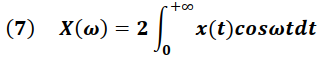
Para "x(t)" impar
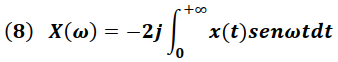
En el caso que se requiera transformar la señal del dominio de la frecuencia al dominio del tiempo, se utiliza la transformada inversa de Fourier dada por:
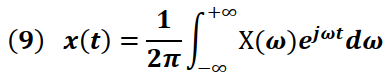
Simbólicamente, la transformada inversa de Fourier es escrita de la forma:
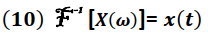
A continuación se muestra la transformada de Fourier de las señales más comunes usadas en las redes eléctricas y sistemas de comunicación.
 Tabla. Transformadas de Fourier de señales básicas
Tabla. Transformadas de Fourier de señales básicas
(Elaborada por @lorenzor en Powerpoint)
Cuando sobre un sistema lineal actúa una señal de entrada, se obtiene una respuesta cuya forma puede ser obtenida a través de la representación en frecuencia del sistema y de las señales actuantes.
Una de las propiedades más importantes de la transformada de Fourier es la propiedad de convolución, la cual establece que en el dominio de la frecuencia la salida de un sistema es el producto de la entrada por la respuesta del sistema (ver figura 1), matemáticamente expresada de la forma:
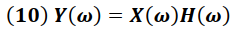
X(ω) → Señal de entrada en Frecuencia
H(ω) → Función de transferencia
Y(ω) → Señal de Salida
 Figura 1
Figura 1
(Elaborada por @lorenzor en Powerpoint)
Esta propiedad pone de manifiesto la importancia de la representación en frecuencia a partir de la transformada de Fourier de un sistema y de las señales actuantes, ya que permite conocer la forma en la que el sistema procesa una determinada señal de entrada para generar una salida.
Una vez obtenida y analizada la salida del sistema en el dominio de la frecuencia, esta puede ser expresada en el dominio del tiempo bajo una transformada inversa de Fourier, según se expresa en la siguiente ecuación:
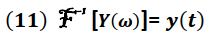
y(t) → Señal de salida del sistema en el dominio del tiempo
A continuación ilustraremos con un ejemplo práctico como obtener, usando la transformada de Fourier, la respuesta de un circuito (sistema) cuando sobre este actúa una señal de entrada.
Ejercicio práctico y Simulación
Determine en el circuito que se muestra en la figura 2 la corriente "Io" usando la transformada de Fourier.
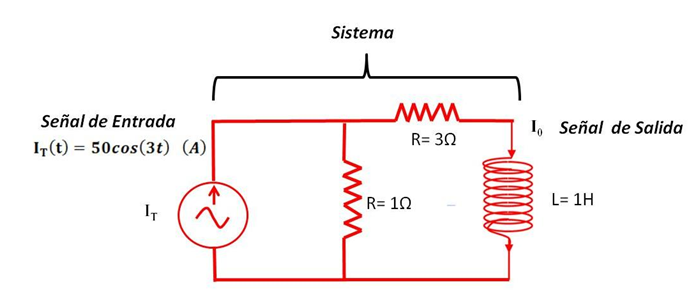 Figura 2
Figura 2
(Elaborada por @lorenzor en Powerpoint)
Solución
Análisis teórico
Dado que la señal de entrada y los parámetros del sistema están expresados en el dominio del tiempo, iniciamos nuestro análisis transformando al dominio de la frecuencia cada uno de estos elementos.
Aplicando la Transformada de Fourier a la señal de entrada, se obtiene (Ver tabla 1):
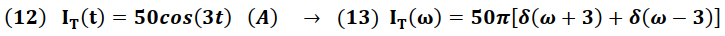
En la siguiente imagen se muestra la transformación a frecuencia de los elementos del sistema:
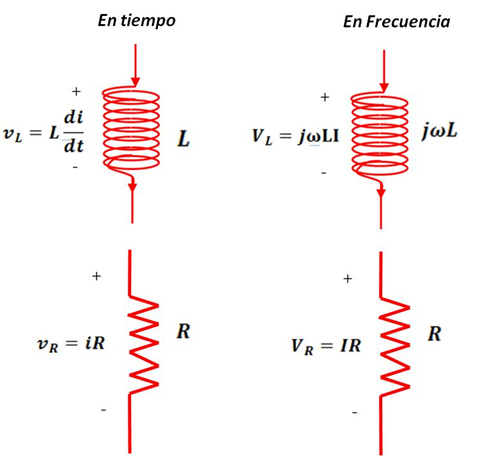 Figura 3. Transformación al dominio de la frecuencia de los elementos pasivos del circuito
Figura 3. Transformación al dominio de la frecuencia de los elementos pasivos del circuito
(Elaborada por @lorenzor en Powerpoint)
Dado que la corriente eléctrica total 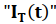 que entra en la asociación en paralelo es dividida, se tiene que:
que entra en la asociación en paralelo es dividida, se tiene que:
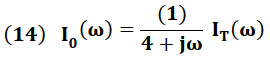 (Divisor de corriente)
(Divisor de corriente)
En la expresión (14) se puede observar que la señal de salida esta dada por la multiplicación en frecuencia de la señal de entrada por la función de transferencia, tal y como lo estable la propiedad de convolución.
De esta forma se tiene que la función de transferencia esta dada por:
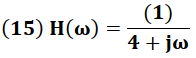
Sustituyendo 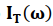 en la expresión (14) se obtiene:
en la expresión (14) se obtiene:
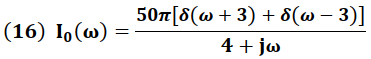
Para obtener la señal de salida I0 (t) en el dominio del tiempo aplicamos la Transformada Inversa de Fourier a la corriente I0 (ω).
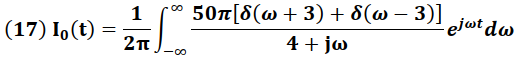
Separando las integrales se tiene:
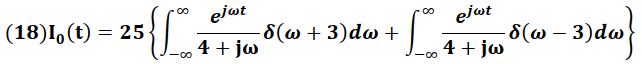
Usando la integral de un Impulso (Delta de Dirac) la cual establece que:
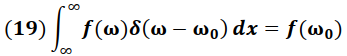
Se puede observar que la función identificada como f(ω) en la integral de la función Impulso esta dada en cada una de las integrales a resolver por la expresión:
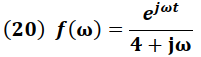
Siendo 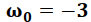 en la primera integral y
en la primera integral y 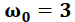 en la segunda.
en la segunda.
De esta forma la solución de cada integral esta dada por la evaluación de la función f(ω) en su correspondiente valor de
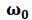
.
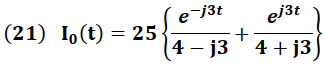
Para una interpretación mas clara de la corriente I0(t) dada por la expresión (21), aplicaremos operaciones matemáticas básicas que permitan reescribir dicha corriente como una señal sinusoidal.
Dado que un número complejo puede escribirse en forma polar según las siguientes ecuaciones:
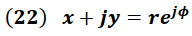
Donde:
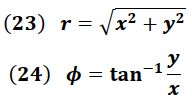
Se tiene que:
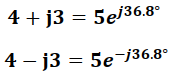
Sustituyendo los números complejos en forma polar en la expresión (21) obtenemos:
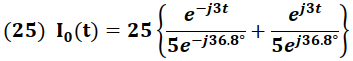
Simplificando se tiene:
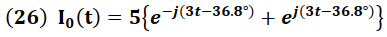
Usando la identidad
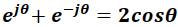
se obtiene finalmente que
I0(t) esta dado por:
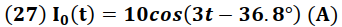
La expresión (27) nos muestra que la salida del sistema presenta un decaimiento en la amplitud de la corriente en comparación con la amplitud de la corriente de entrada, cuya amplitud es de 50 (A), presentado además un desfasaje de 36.8ᵒ respecto a la señal de entrada.
Simulación
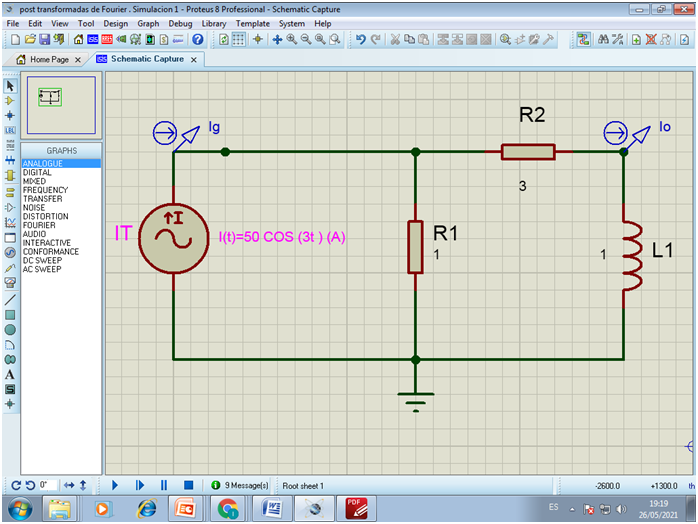
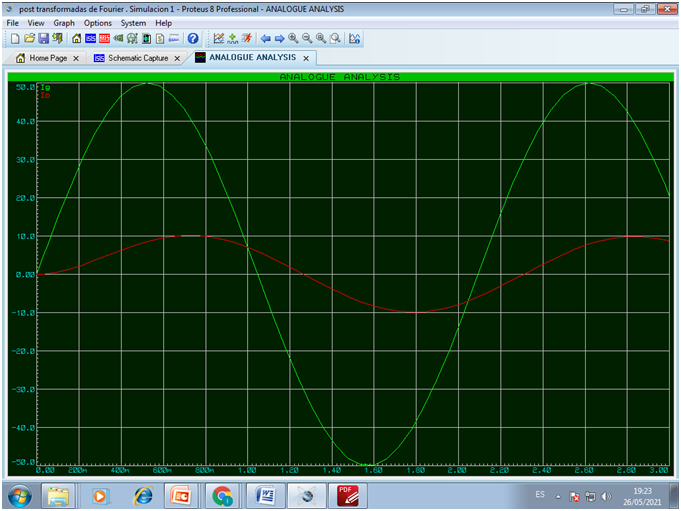
Con la finalidad de validar el análisis teórico desarrollado en este trabajo y los resultados obtenidos, se realizó la simulación del circuito ejemplo utilizando el simulador de circuitos Proteus versión 8, donde se puede apreciar que la señal de salida presenta una disminución en su amplitud y un desfasaje respecto de la señal de entrada, lo cual está en total correspondencia con el resultado obtenido en nuestro desarrollo teórico.
Gracias por leer mi publicación, espero que el análisis realizado en este trabajo permita fortalecer y consolidar sus conocimientos en el estudio de redes eléctricas.
Si tienes alguna duda, pregunta o sugerencia deja tus comentarios y con mucho gusto te responderé.
Referencias
- Circuitos Eléctricos. James W. Nilson. Cuarta edición. Addison-Wesley Iberoamericana.
- Física Vol. II Campos y ondas. Marcelo Alonso, Edward J. Finn. Fondo Educativo Interamericano, S.A.
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert.
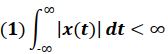
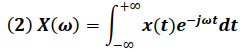
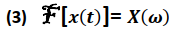
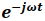 , se tiene:
, se tiene: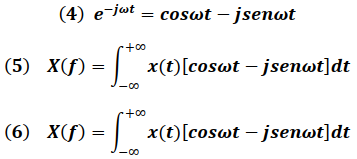
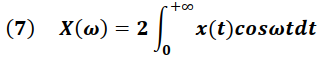
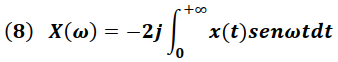
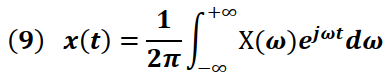
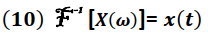

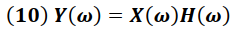

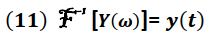

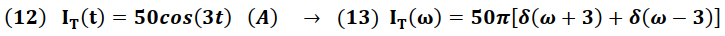

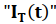 que entra en la asociación en paralelo es dividida, se tiene que:
que entra en la asociación en paralelo es dividida, se tiene que: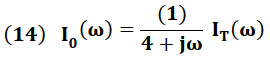 (Divisor de corriente)
(Divisor de corriente)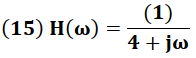
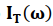 en la expresión (14) se obtiene:
en la expresión (14) se obtiene: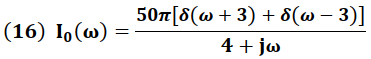
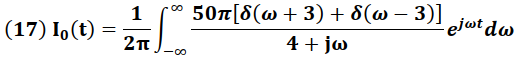
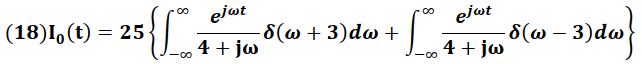
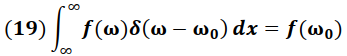
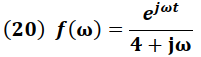
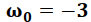 en la primera integral y
en la primera integral y 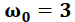 en la segunda.
en la segunda.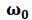 .
. 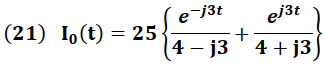
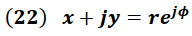
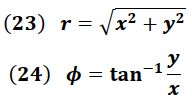
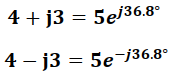
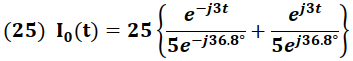
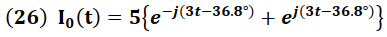
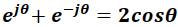 se obtiene finalmente que I0(t) esta dado por:
se obtiene finalmente que I0(t) esta dado por: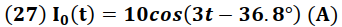


Excelente desarrollo tanto conceptual como práctico usando la Transformada de Fourier. En pensar que actualmente mucha de la tecnología que a diario utilizamos tiene sus cimientos a Fourier. Gracias @lorenzor por entregar en su post estas guías.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Congratulations @lorenzor! You received a personal badge!
You can view your badges on your board and compare yourself to others in the Ranking