¡Hola amigos de Hive blog!
Reciban un cordial saludo.
El diseño de los componentes y dispositivos utilizados en sistemas electrónicos y redes eléctricas han sido posible gracias a los principios y fundamentos derivados del electromagnetismo.
El capacitor es uno de los componentes basado en estos principios y debido a su amplia gama de aplicaciones es un elemento esencial en todos los sistemas electrónicos.
Dada su importancia, analizaremos los principios y fundamentos de este dispositivo y abordaremos algunas de sus aplicaciones en el campo de la ingeniería.
Un Capacitor es el arreglo o combinación de conductores separados por un aislador (vació, aire o un material dieléctrico), sometidos a una diferencia de potencial y cuya configuración permite el almacenamiento de carga y energía potencial eléctrica.
Los capacitores más comunes son capacitores de placas paralelas, cilíndrico y esférico. (Ver figuras 1, 2 y 3)
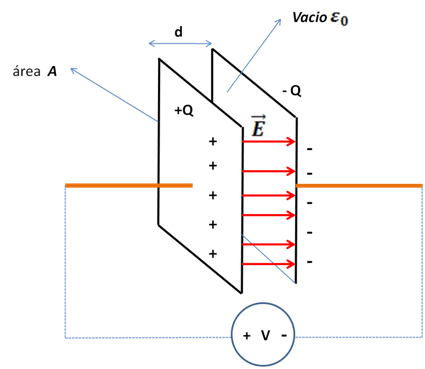
(Elaborada por @lorenzor en Powerpoint)
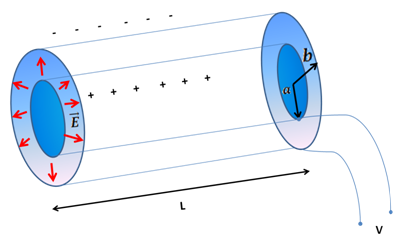
(Elaborada por @lorenzor en Powerpoint)
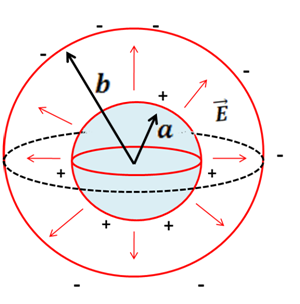
(Elaborada por @lorenzor en Powerpoint)
La diferencia de potencial aplicada a los dos conductores aislados es proporcional a la carga almacenada. Esta constante de proporcionalidad es conocida como la capacitancia del capacitor, lo cual se expresa matemáticamente de la siguiente forma:
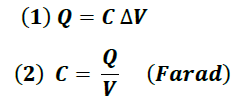
Donde “Q “es la magnitud de la carga en cualquiera de los conductores y "∆𝑽 " representa la magnitud de la diferencia de potencial aplicada (por simplicidad denotada como "𝑽 " ).
Si bien la expresión 2 permite obtener la capacitancia en cualquier capacitor, la determinación de la diferencia de potencial en cada uno de los tipos de capacitores antes mencionados permite obtener a una expresión alternativa de la capacitancia.
Esta diferencia de potencial en cada tipo de capacitor es obtenida usando la ley de Gauss, de la que se obtiene las siguientes expresiones:

ε0 → Permitividad eléctrica del espacio libre


Las expresiones 3, 4 y 5 combinadas con la expresión 2 conducen a las siguientes ecuaciones alternativas de la capacitancia:



Considerando que la permitividad eléctrica del espacio libre (vació) es una constante universal, se puede observar que la capacitancia en cada uno de los modelos analizados es una función de su geometría, indicando de esta forma que la Capacitancia es independiente de la carga y de la diferencia de potencial aplicada.
Si el espacio entre los conductores está constituido por un material dieléctrico (Ver figura 4), la polarización que este experimenta induce un campo eléctrico “ Ei ” en la región que separa ambos conductores que es opuesto al campo eléctrico entre las placas, lo cual se traduce en una disminución del campo eléctrico total y por ende en una disminución en la diferencia de potencial, conduciendo finalmente a un aumento en la capacitancia que es proporcional a la permitividad eléctrica del material, tal y como se muestra en la siguiente expresión:
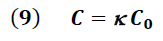
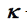 → Constante dieléctrica del material (adimensional)
→ Constante dieléctrica del material (adimensional)
C0 → Capacitancia en ausencia de dieléctrico
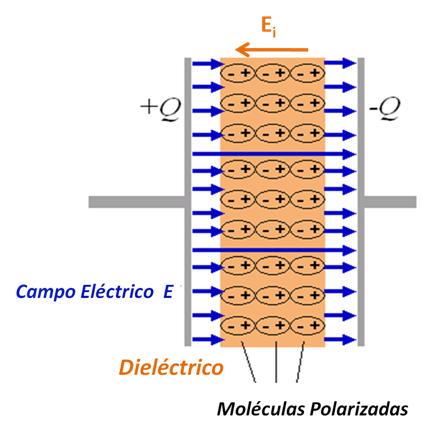
Wikimedia commons
( Imagen de dominio público modificada por @lorenzor)
Los materiales dieléctricos además de representar un aumento en la capacitancia, tienen un mayor rango de soporte en las intensidades de campos eléctricos minimizando el rompimiento o destrucción del capacitor.
Una vez almacenada la energía eléctrica en los capacitores, esta se conservará durante un largo tiempo. Esta energía almacenada es utilizada para ser descargada sobre otros elementos del circuito por periodos de tiempos controlados.
Muchas de las tecnologías actuales funcionan gracias a estos dispositivos. Las computadoras, telefonía, sistemas eléctricos automotriz, sistemas de TV, etcétera.
En la siguiente figura se observa la aplicación de un capacitor de placas paralelas con las que operan una gran variedad de teclados de computadores.
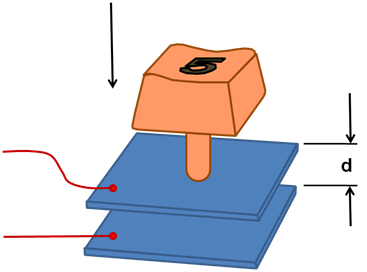
(Elaborada por @lorenzor en Powerpoint)
Cuando presionamos la tecla superior, la variación en la distancia “d” produce una variación en la capacitancia, generando a su vez un impulso de carga o corriente eléctrica desde el capacitor (tecla) hacia el circuito maestro del computador.
En el laboratorio de pruebas contamos con prototipos de capacitores con los que se analizan las distintas variables que intervienen en su funcionamiento (ver Figura 6).
En el campo de la investigación son utilizados en la caracterización de materiales.

(Fotografía tomada por @lorenzor)
De esta forma podemos apreciar que el capacitor en cualquiera de sus formas y tipos es uno de los componentes cuyas propiedades lo han convertido en un elemento vital en una gran variedad de sistemas.
Referencias
- Introduction To Electromagnetic Fields Third Edition / Clayton R. Paul, Keith W. Whites, Syed A. Nasar
- Electrodinámica Clásica Segunda Edición / John David Jackson
- Electromagnetismo Conceptos y Aplicaciones Cuarta Edición / Stanley V. Marshall, Richard E. DuBroff, Gabriel G. Skitek
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert
- Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo II. McGraw-Hill.
- Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 2. Addison Wesley Longman.
- Teoría electromagnética. Willian H. Hayt, Jr., John A. Buck. Séptima edición. McGraw Hill.
Has sido votado por
PROYECTO ENLACE
'Conectando Ideas y Comunidades'
PROYECTO ENLACE es un proyecto de curación de habla hispana enfocado en recompensar contenido de calidad y apoyar autores en su proceso de crecimiento en HIVE.
Creemos y apostamos por el futuro de esta gran plataforma, y estamos muy emocionados de poder hacerla crecer junto a esta comunidad. Así que te invitamos a usar nuestra etiqueta ENLACE y estar atento a todas las actividades que tenemos preparadas y que estaremos publicando en breve.
Te invitamos a participar en nuestro servidor de Discord: https://discord.gg/3S9y7BbWfS
Atentamente
EQUIPO ENLACE 2020
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.