
Father of the Powerful Mordell Curves
It was on 12 March 1972 that the prominent American-born British mathematician died in Cambridge, England. Louis Joel Mordell was widely recognised by the mathematical community for his great contributions to the theory of numbers, since he made important mathematical developments that served to deepen two very important areas of study for the theory of numbers and mathematics in general, such as the study of Diophantine equations and elliptic curves, both of which are now fundamental pillars of recent technological development.
At present, Diophantine equations and elliptic curves are tools of vital importance within the structure of scientific-technological fields such as cryptography, where they are often found in several types of mathematical algorithms used for encryption and key encryption within the banking system, just to mention one of the many cases of use where such mathematical developments have been largely driven by the work of Mordell.
Main Mathematical Contributions.
The Mordell-Weil Theorem:
First, Louis Mordell succeeded in proving the theorem that bears his name, which states that the group of rational points on an elliptic curve is finitely generated. Later, this result achieved by Mordell was generalised by the French mathematician Andre Weil, which gave rise to the conception of the Mordell-Weil theorem, a cornerstone in the study and applications of elliptic curves.Mordell's Conjecture:
Mordel's conjecture states that for an algebraic curve of genus greater than one there are only a finite number of rational points. This conjecture was later proved by the German mathematician Gerd Faltings in 1983.Diophantine Equations:
Mordell's research in the field of diophantine equations was of a very extensive nature, and was of vital importance to the advancement of mathematics in this field, with his contribution to the in-depth study of the famous Mordell equation, which has the form y2 = x3 + n, for any natural n.Modular Forms:
Professor Mordell's mathematical contributions to the study of modular forms do not go unnoticed within the mathematical community either, as he had a very prolific participation in the development of this research topic, highlighting his mathematical proof achieved in 1917, which responds to a conjecture set up by the Hindu genius of mathematics, Srinivasa Ramanujan, and which is based on the study of the Tau function.
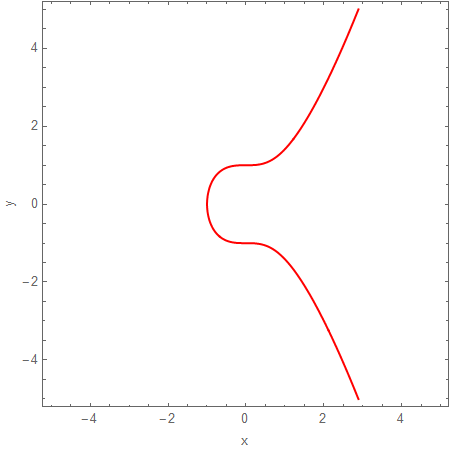
A Mordell Curve
Life and Performance.
On 28 January 1888, Louis Joel Mordell was born in the American city of Philadelphia. After finishing high school, he left for the United Kingdom, more specifically to England, with the aim of studying mathematics at the transcendent University of Cambridge, where he succeeded the great British mathematician G.H. Hardy as professor of the same chair of mathematics at Cambridge in 1945.
In addition to his distinguished career as an academic at Cambridge University, he also held professorships at Birkbeck College London and Manchester University. Professor Mordell was well known in academia for his independent style of work and his intense dedication to mathematical research at the highest level.
He was also a great Samaritan, taking in many mathematicians and scientists fleeing the war, most notably the mathematicians Paul Erdos and Kurt Mahler.
Key Publications:
'Diophantine Equations' (1969):
This work is a book that is considered today as a fundamental work for the study of Diophantine equations, since in it, Mordell makes a compilation and exposition of his research in this field, as well as that of other mathematicians experts in this type of equations.The book has served as a reference for generations of number theorists, due to its clarity and depth in the topics that this book covers. Within this book we can find topics ranging from linear and quadratic Diophantine equations to complex equations of higher degrees and elliptic curves.
Publications in Mathematical Journals:
Throughout his career as a professional mathematician, Mordell published numerous mathematical research articles in multiple mathematical journals that had and still have great prestige within the mathematical community.Anyone can get an idea of the magnitude of the articles published by Professor Mordell if one reviews the references available on the St. Andrews University website.
Undoubtedly, even today the weight of Mordell's mathematical work continues to be felt within the mathematical and scientific community in general, where his work on Diophathine equations and elliptic curves laid the foundations for the continuation and deepening of mathematical research and subsequent applications that have these topics as their foundations. which have led to important technological developments related to computer science and cryptography, both of which are fundamental fields of study for the development of modern technological society.
Finally, and as is customary in previous posts, there is no other option than to thank and surrender to the greatness of your work, Professor Mordell.

Some of His Contributions.



Note: All the images related to Mordell Contributions are crafted by me using the text editor based on LaTeX: Beamer. Also, the plots about the Elliptic Curves shown in this post were created by me using the Wolfram language: 'Mathematica'.
'The Structure of this article is by my authorship too.'
Regards.
References
Silverman, Joseph H. (1986). The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics. Vol. 106. Springer-Verlag. doi:10.1007/978-0-387-09494-6. ISBN 0-387-96203-4. MR 2514094.
Weisstein, Eric W. "Mordell Curve." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/MordellCurve.html

The rewards earned on this comment will go directly to the people( @paultactico2 ) sharing the post on Reddit as long as they are registered with @poshtoken. Sign up at https://hiveposh.com. Otherwise, rewards go to the author of the blog post.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.
Hey thank you as always for the support, stemsocial team. I have delegated some hp to the stemsocial acount :)
Regards.