Cuantos conocimientos esparcidos por nuestro universo, conocimientos de vital utilidad para nuestra existencia, si miramos a nuestro alrededor de seguro que somos testigos fidedignos de cualquier clase de transmisión de un determinado movimiento, esta característica de transmisión nos ha permitido constituir mecanismos mucho más complejos y, sobre todo, mucho más útiles en cada una de nuestras actividades.
A pesar que la era o el tiempo de la digitalización a llegado en nuestras vidas, sin embargo, son muchos los componentes mecánicos de gran ayuda en las distintas actividades del hombre, por ejemplo, el movimiento descripto en el gif al inicio de esta presentación es muestra de la utilización de esta transmisión de movimientos, muchos de estos mecanismos permiten poder trasladar cualquier cantidad de objetos de un lugar a otro si tener que utilizar esfuerzo físico humano.
Este tipo de movimiento circular uniforme lo podemos notar en cualquier lugar donde nos encontremos y, es por ello, que en esta oportunidad he querido resaltar su importancia y, además, la importancia de las matemáticas a través de sus formulaciones que han permitido comprender el fenómeno del movimiento en sus distintas representaciones y acciones, por lo tanto, a continuación les comparto otro interesante ejercicio práctico donde gracias al nexo de las matemáticas y la física hemos podido comprender a mayor profundidad.
Ejercicio
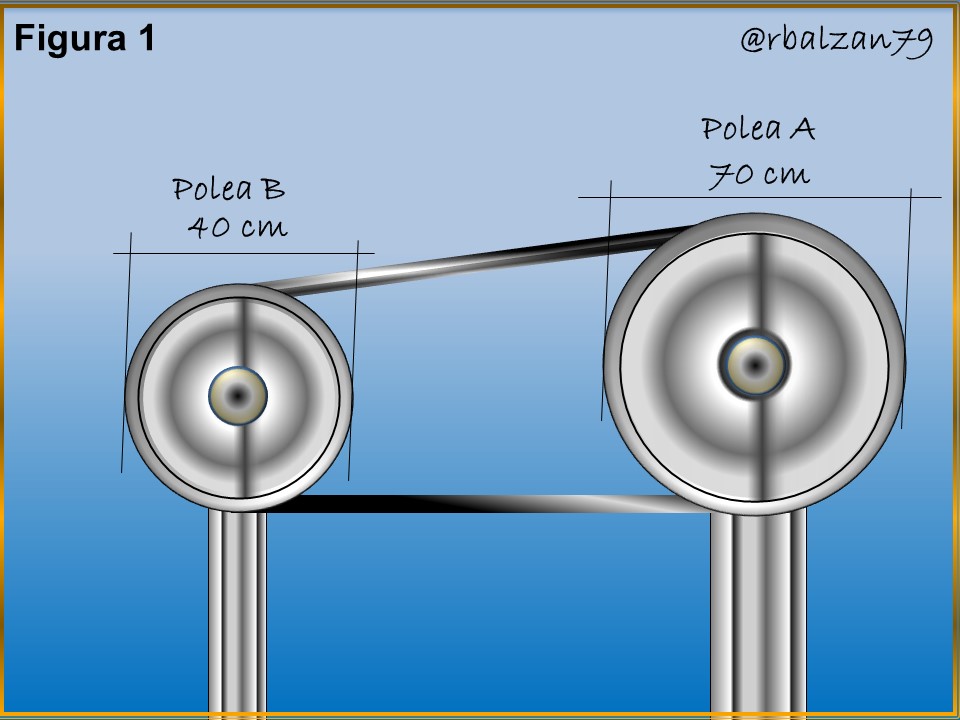
Mediante una transmisión de movimiento, observamos a dos poleas o ruedas unidas por una determinada correa o cuerda, donde, una posee un diámetro de 70 cm y la otra de 40 cm, la polea (A) de mayor diámetro gira a una frecuencia de 18 Hertz (Hz), por lo tanto, es importante que podamos responder a las siguientes interrogantes:
a.- ¿Cuáles serán las velocidades angulares (ω) de las poleas?
b.- ¿Cuáles serán las velocidades lineales de las poleas?
Datos:
RA = D/2 = 70/2 = 35 cm = 0,35 m (Radio de la polea A).
RB = D/2 = 40/2 = 20 cm = 0,20 m (Radio de la polea B).
fA= 18 Hz (Frecuencia de la polea A)
ωA = ? (Velocidad angular de la polea A).
ωB = ? (Velocidad angular de la polea B).
VA= ? (Velocidad lineal de la polea A).
VB=? (Velocidad lineal de la polea B).
Solución
a.- Para iniciar a responder nuestra primera incógnita podemos comenzar a conocer nuestra primera fórmula.

Observamos que en los datos suministrados poseemos una de las frecuencias, es decir, la frecuencia de la polea A, por lo tanto, antes de calcular la velocidad angular de esta polea podemos aplicar la siguiente relación:

De esta relación procedemos a despejar la frecuencia de la polea B, como se muestra a continuación:

Ahora con esta fórmula 3, podemos conocer la frecuencia de la polea de menor diámetro, es decir, la polea B y, para ello, realizamos los siguientes cálculos:
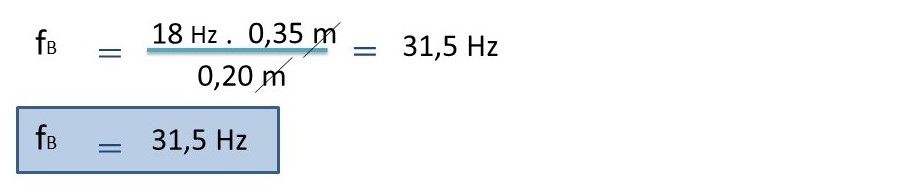
Con este valor de la frecuencia de la polea B, pasamos a calcular cada una de las velocidades angulares (ω) de las poleas, por lo tanto, tenemos:

b.- Pasamos de esta manera a nuestra segunda interrogante, es decir, calcular las velocidades lineales o tangenciales de ambas poleas y, para ello, vamos a conocer la siguiente fórmula:
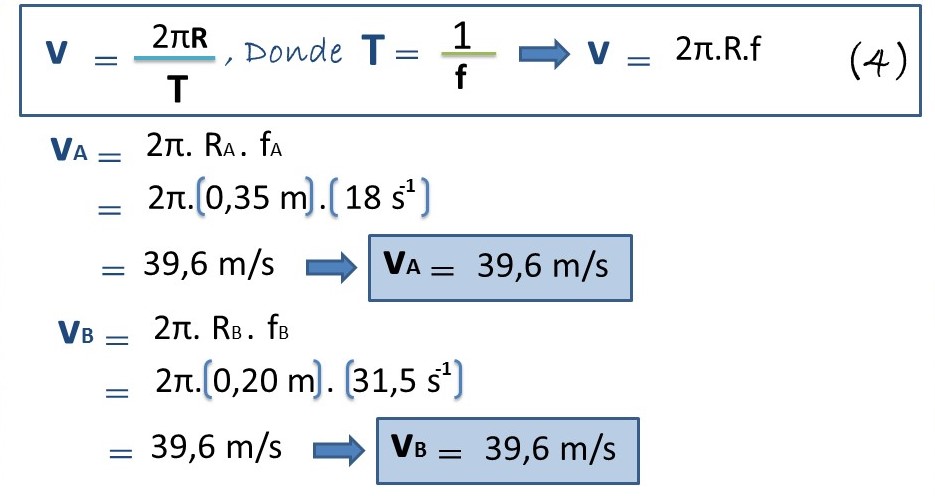
De esta manera podemos comprobar el movimiento circular uniforme ya que la velocidad es constante (39,6 m/s), en todo el sistema de poleas.
Conclusión
En realidad, el movimiento circular lo podemos observar en cualquier espacio-tiempo donde nos encontremos y, el mismo es de gran utilidad, en esta ocasión logramos calcular interesantes variables físicas de una transmisión de movimiento entre dos poleas, tales como velocidad angular y velocidad lineal de ambas poleas, donde además, logramos calcular una de las frecuencias faltante (31,5 Hz) de una de las poleas (B), y la misma resulto mayor que la frecuencia de la otra polea (A), esto es debido a que por ser la polea (B) de menor diámetro tiene la posibilidad de girar con mayor frecuencia que la polea (A) de mayor diámetro, de hecho si calculamos los periodos (T) de cada polea podemos notar como la polea de menor diámetro (B) utiliza menos tiempo en completar un ciclo que la polea de mayor diámetro (A), como pueden observar a continuación:
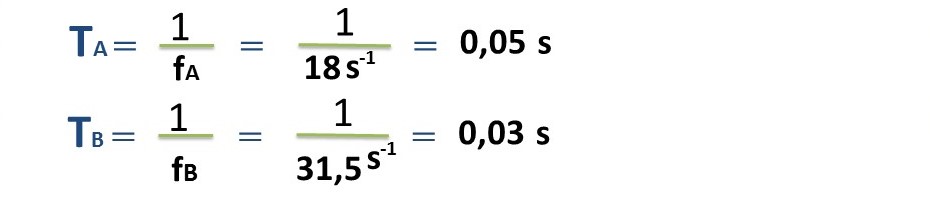
Esto también influye en la velocidad angular de dichas poleas como pudieron notar anteriormente. A pesar que tanto las frecuencias como las velocidades angulares resultaron distintas, la velocidad lineal resulto ser la misma por tratarse de un movimiento circular uniforme, interesantes características que pudimos analizarlas por el hecho de implementar importantes formulaciones matemáticas.
Hasta otra oportunidad mis queridos amigos.
Nota: Las imágenes fueron realizadas por el autor utilizando Power Point y Paint, el gif animado fue creado utilizando la aplicación de PhotoScape.
Referencia Bibliográfica recomendada
[1] Olmedo Santiago. Manual de Cinemática y dinámica. Universidad Politécnica Salesiana. Año 2012. Link.
[2] Movimiento circular uniforme. Link.
Congratulations @rbalzan79! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 900 posts.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Check out our last posts:
Support the HiveBuzz project. Vote for our proposal!
¡Hola amigo rbalzan79!
Gracias por compartir la información, muy práctica y detallada.
Hola estimada amiga @yusvelasquez, gracias por tu visita y comentario. Saludos.