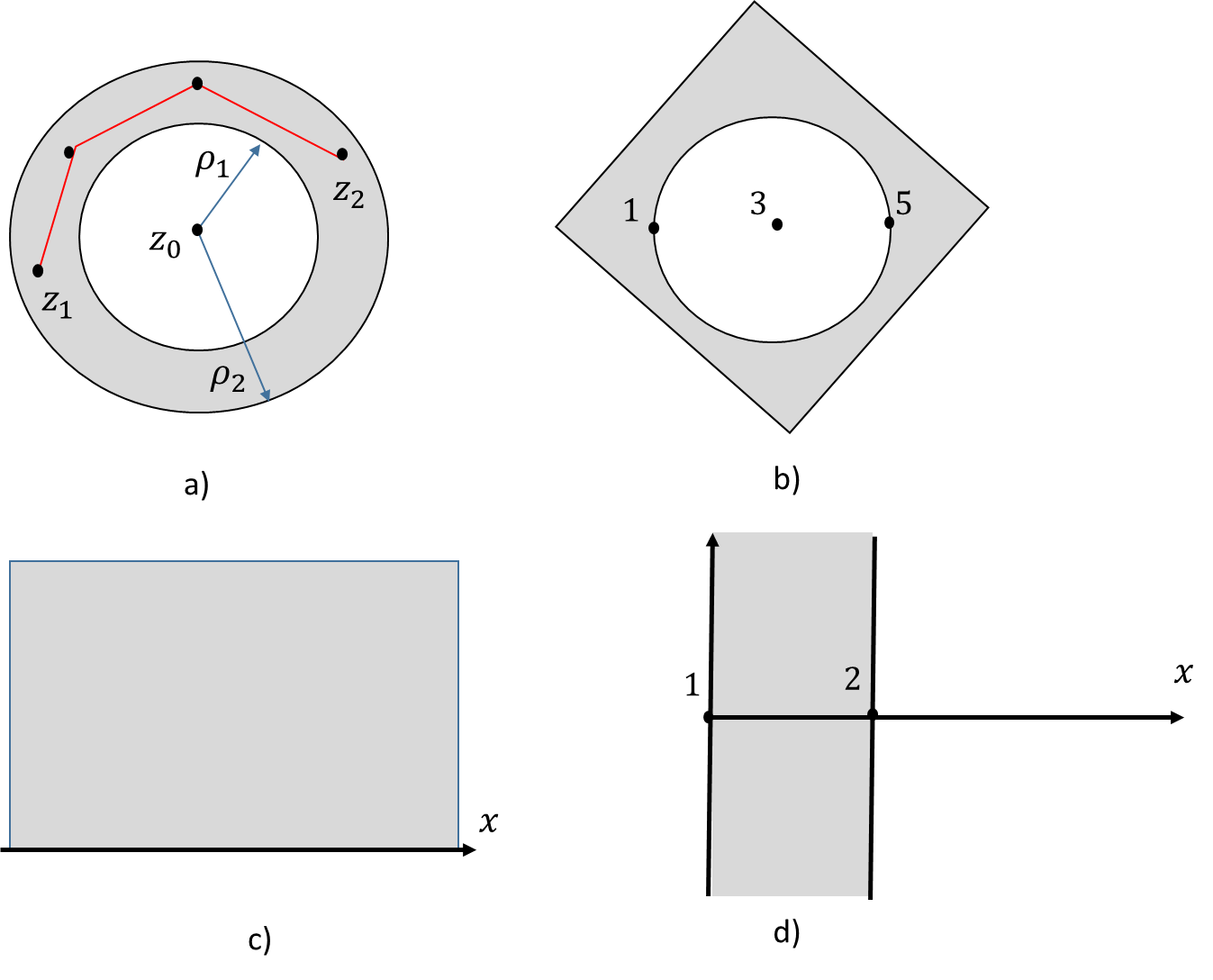
Conjunto de puntos en el plano complejo
Los teoremas fundamentales de las variables reales están bien establecidos y definidos por funciones que pertenecen a un intervalo abierto o cerrado. Las funciones de variables complejas están formuladas y definidas en un conjunto que pertenece al dominio de dos dimensiones o regiones cerradas.
El conjunto de todos los puntos que satisfacen la ecuación

es llamado disco abierto o vecindad circular de 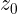

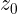

son vecindades circulares de los respectivos puntos 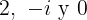
Llamaremos la vecindad de disco unitario abierto a la siguiente expresión

Un punto 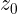
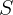
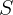
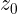
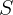 es la mitad derecha del plano
es la mitad derecha del plano  y
y  , entonces
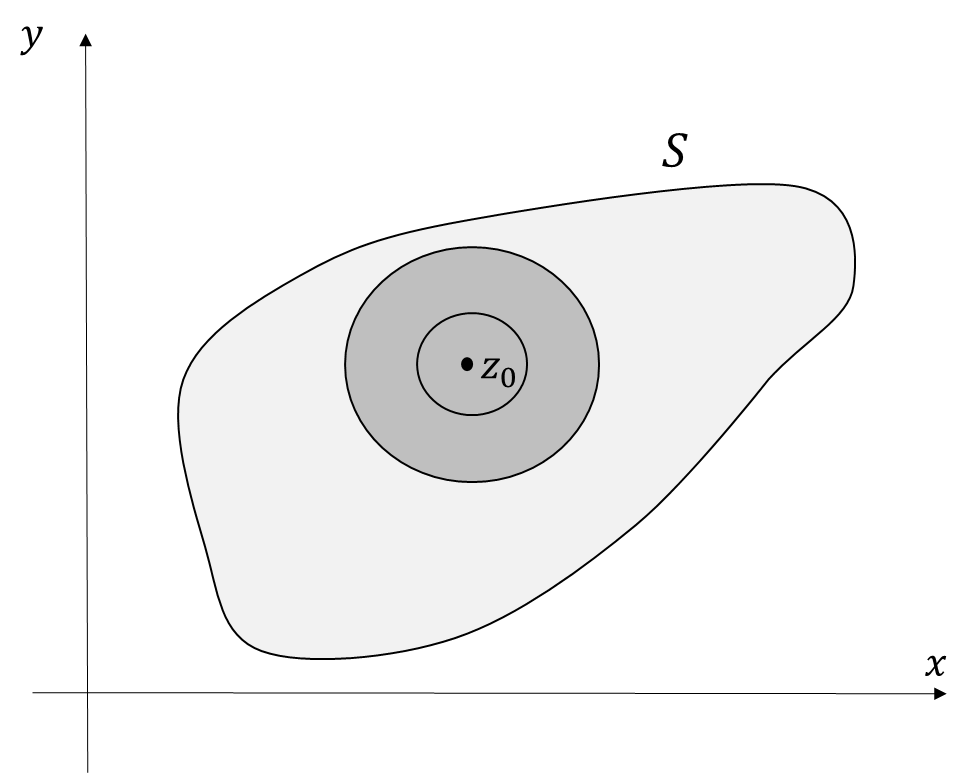
, entonces 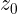 es un punto interior de
es un punto interior de 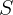 porque este conjunto contiene la vecindad
porque este conjunto contiene la vecindad 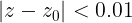 (Ver figura)
(Ver figura)

Si cualquier punto de 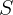
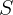
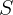
Cada una de las siguientes inecuaciones también describen un conjunto abierto
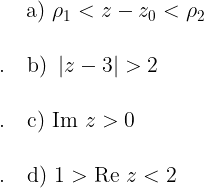
Esbocemos estos conjuntos en las siguientes figuras

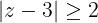 no es un conjunto abierto ya que no existen puntos sobre el círculo,
no es un conjunto abierto ya que no existen puntos sobre el círculo,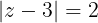 es un ´punto interior de T. Note también que un intervalo abierto del eje real no es tampoco un conjunto abierto ya que este no contiene el disco abierto.
es un ´punto interior de T. Note también que un intervalo abierto del eje real no es tampoco un conjunto abierto ya que este no contiene el disco abierto.
Tenemos 
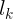





Un conjunto abierto 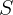

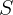
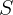
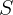
El conjunto que consiste de todos los puntos en el plano que no están en el círculo 
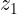

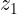

Un conjunto conectado abierto lo llamamos un dominio. Por lo tanto todos los conjuntos de las fihuras anteriores a), B9, c) y d) son dominios.
En el cálculo de funciones de una variable real simple un hecho útil y familiar es que, sobre un intervalo, la cancelación de una derivada indica que la función es identicamente cosntante. Ahora presentamos una extensión de este resultado para dos variables reales, lo cual sobresalta la importancia de la noción de dominio.
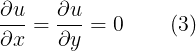
Observemos que la asunsión 



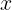







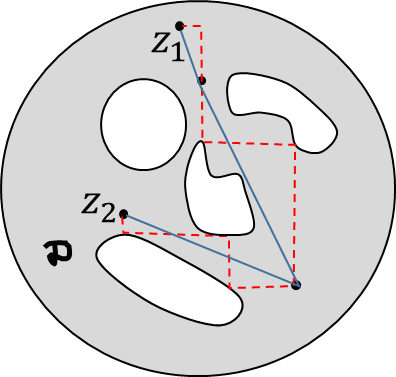
 es asumido solo para ser un conjunto abierto, ya que entonces por partes cosnstantes las funciones pueden sayisfacer la hipótesis.
es asumido solo para ser un conjunto abierto, ya que entonces por partes cosnstantes las funciones pueden sayisfacer la hipótesis.
Ejemplo 1.
Un valor real de la función 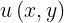

En cualquier punto del disco abierto 

Solución.
Sea 
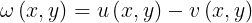
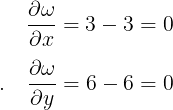
En cada punto de 



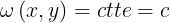

lo cual es lo pedido por la fórmula de 
Un punto 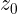
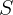
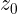
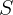
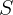
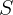
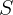
Las fronteras de los conjuntos esbozados en las figuras anteriores a), b) c) y d) son:
a) Los dos círculos 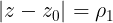

b) El círculo 
c) Eleje real.
d)Las líneas 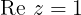



Un conjunto se dice que es cerrado si este contiene todos los puntos frontera.
El conjunto descrito por la ecuación 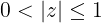
El conjunto de puntos 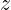

es un conjunto cerrado ya que contiene su frontera 
Un conjunto 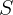


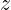
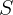
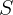
Un conjunto ilimitado es uno que no es límite. De los conjuntos de las figuras anteriores, solo a) es límite.
Un conjunto que es cerrado y límite se dice que es compacto.
Una región es un dominio junto con algún, ninguno o todos estos puntos frontera. En particular, cualquier dominio es una región.
Bibliografía
- Churchill R., Brown J., Verhey R. Complex variables and applications. 3th. Ed. McGraw-Hill, New York, 1976.
- Spiegel M. Variable compleja. McGraw-Hill (Serie Schaum), México, 1971.
- Saff E., Snider A. Fundamentals of complex analysis. Prentice Hall, 3th. Ed. 2003.
- Volkovyski L., Lunts G., Aramanovich I. Problemas sobre la teoría de funciones de variable compleja. MIR, Moscú, 1984.
Fuente de las imágenes
Todas las imágenes fueron hechas por mi usando el software PowerPoint.





Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.