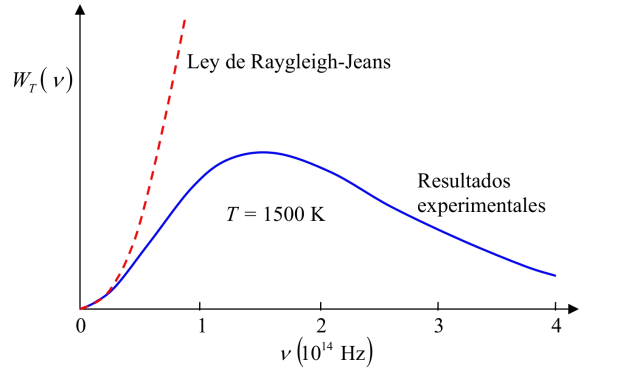
Radiación de cuerpo negro. Teoría clásica de Rayleigh
En mi post más reciente Ver post, comencé a abordar el tema de la radiación de cuerpo negro, este fenómeno físico tenía a los científicos a finales del siglo XIX con los pelos de punta ya que la teoría no coincidía con los experimentos. En este post continúo con lo que fue aquella búsqueda de la verdad que condujo a la mecánica cuántica.
Comenzando el siglo XX el físico inglés J. W. S. Rayleigh trató de descifrar el enigma de la radiación de cuerpo negro, él tuvo la idea de que la radiación consistía en ondas estacionarias que poseían una temperatura T con nodos en la superficie metálica del objeto y las cuales eran equivalentes a los osciladores armónicos de los electrones presentes en la cavidad. Al llegar al equilibrio termodinámico la densidad energética electromagnética en el interior de la cavidad es la misma que la de las paredes, de tal manera que, en promedio, la radiación total se puede calcular multiplicando la energía de los osciladores, promedio, por el número de nodos, es decir, las ondas estacionarias de la radiación en un intervalo de frecuencia dado por el un valor de frecuencia más esa frecuencia y un diferencial de la misma.
Pero, vamos a analizar con detenimiento a que se refería Rayleigh con esta teoría. Vamos a suponer que las paredes metálicas de la cavidad, con radiación electromagnética, tienen la forma geométrica de un cubo (Ver Figura abajo), aquí la radiación que se refleja en las paredes la podemos estudiar en términos de los tres ejes coordenados x, y y z los cuales son independientes el uno del otro.

Como los planos que forman las paredes son paralelos entre sí, las componentes de la radiación no interactúan entre sí y se pueden analizar por separado. Comencemos considerando la componente x en x=0, de tal manera que la radiación que incida en esta pared será reflejada y entonces las ondas incidentes y reflejadas se combinarán para formar una onda estacionaria. Por la teoría electromagnética sabemos que la radiación es una onda transversal con un vector de campo eléctrico normal a la dirección de propagación, pero esta última es perpendicular a la pared que estamos considerando, entonces el campo eléctrico será paralelo a dicha pared, sin embargo, la superficie de una pared metálica siempre tendrá un flujo de cargas que neutralizará el campo eléctrico paralelo a ella, es decir, el campo eléctrico será nulo en la pared y por lo tanto la onda estacionaria en dirección x será un nodo de amplitud cero, x=0 y esta onda debe tener otro nodo en x=a, esto es lógico, ya que un campo eléctrico paralelo a la pared no puede existir.
El análisis riguroso anterior se aplica también a las compontes en y y z, por lo tanto deben haber nodos en y=a, z=a. Todas estas condiciones establecen e imponen limitaciones en las longitudes de onda que se pueden producir y obviamente a sus frecuencias respectivas. Luego de esto debemos ser capaces de saber el número de ondas estacionarias con nodos en la superficie de la cavidad que se encuentran en los intervalos (v, v+dv).
Trataremos solo la componente x para enfocarnos en estos cálculos, es decir, el caso hipotético de una cavidad en una dimensión de longitud a, hacemos esto porque luego se verá que al llevar esto al caso real tridimensional es obvio.


La onda por ser estacionaria tendrá nodos fijos en ella. Ahora necesitamos satisfacer la condición de borde, escogemos el origen del eje x en uno de los extremos de la cavidad x=0 y x=a, entonces
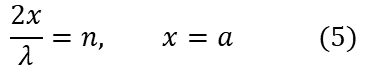
Esta expresión nos proporciona el conjunto de valores permitidos de la longitud de onda, para que la amplitud de la longitud de onda estacionaria siga un comportamiento como el que se muestra en la figura de abajo.
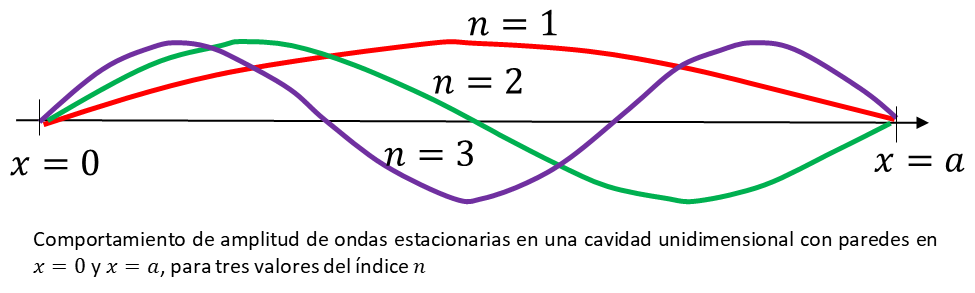
Vamos ahora a trabajar con frecuencias en vez de longitudes de onda, es decir,
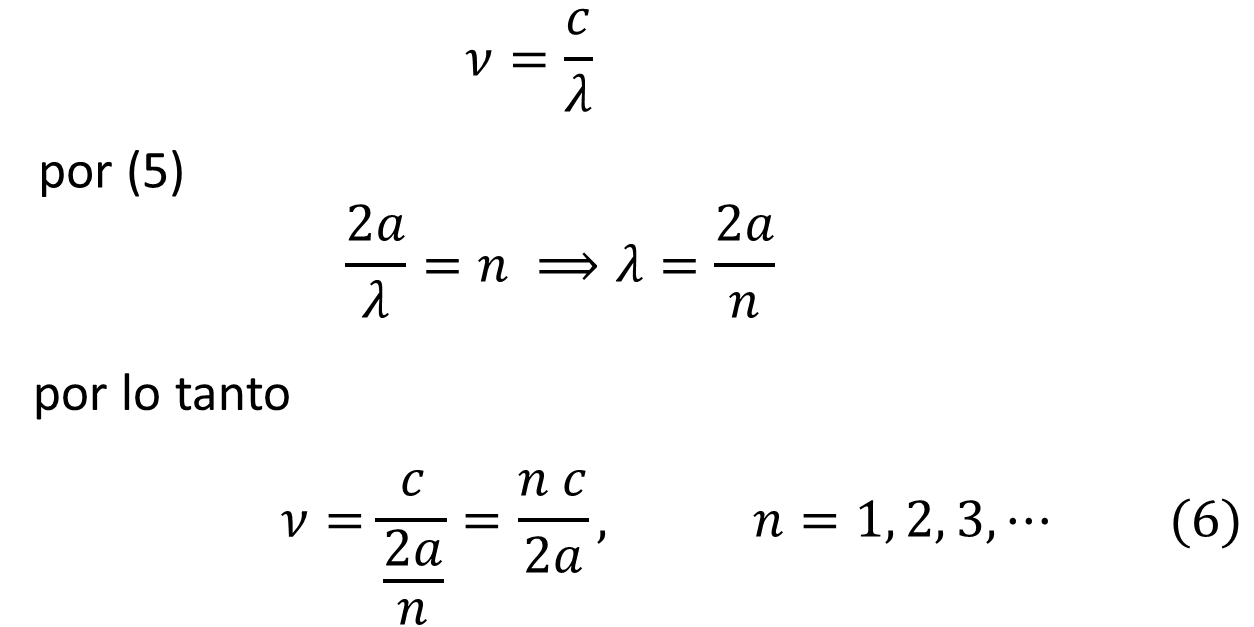
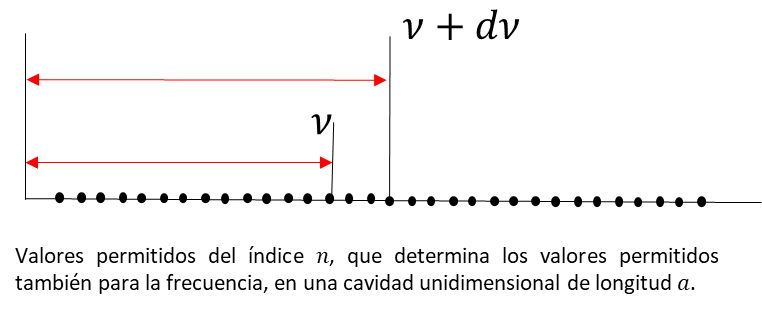
Podemos representar mediante un diagrama los valores permitidos de las frecuencias, este consiste de puntos discretos sobre un eje que corresponden a cada valor entero de n, de acuerdo a la ecuación (6), estas relaciones se muestran en la siguiente figura.
La ecuación final obtenida por Rayleigh fue la siguiente

En el próximo post relacionado con este tema continuaremos con el desarrollo que efectúo Rayleigh en el intento por conseguir una ecuación teórica que diera la respuesta al enigmático espectro de la radiación de cuerpo negro.
Bibliografía
- Eisberg R. Quantum physics of atoms, molecules, solids, nuclei and particles. 2nd Ed. John Wiley & Sons. New York, 1985.
- Zettili N. Quantum mechanics. Concepts and applications. Wiley, 2009.
- Shankar R. Principles of quantum mechanics. 2nd Ed. Plenum Press. New York, 1994.
- Liboff R. introductory quantum mechanics. 4th Ed. Addison Wesley, 2003.
- Gasiorowicz S. Quantum physics. 3th Ed. John Wiley & Sons, 2003.
- Feynman R. P. Física. Volumen III: Mecánica cuántica. Bilingua, Bogotá, 1971.
Fuente de las imágenes
- Portada. Radiación de Rayleigh-Jeans. Fuente
Todas las demás imágenes fueron tomadas de la bibliografía señalas y otras hechas por mi utilizando el software Microsoft PowerPoint.


Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.