
Imagen del átomo de dominio público disponible aqui, logo diseñado por @stem-espanol
Un gran saludo a las comunidades de #stemsocial y #stem-espanol, retomando las publicaciones sobre cálculo numérico, el día de hoy iniciaré esta serie de post que tratarán sobre la implementación de los métodos numéricos en el lenguaje de programación JavaScript.
SOBRE EL CÁLCULO NUMÉRICO
El cálculo numérico, también denominado análisis numérico trata sobre los métodos numéricos que permiten obtener aproximaciones bastantes precisas a los resultados obtenidos usando el análisis matemático, de esta forma se pueden obtener los valores de Derivadas e Integrales sin necesidad de resolverlas de forma analítica.
El cálculo numérico hace uso de distintos procedimientos matemáticos y en la mayoría de los casos se vale de herramientas computacionales para desarrollar algoritmos que permitan implementar los conceptos analíticos y llegar a resultados numéricos.
¿Por qué en JavaScript?
En general los métodos numéricos suelen desarrollarse utilizando sistemas de Álgebra Computacional (CAS por sus siglas en inglés Computer Algebra System), tales como Maxima, Scilab, MathLab, en esta serie de artículos se realizarán en el lenguaje de programación web JavaScript.
JavaScript (JS) según MDN contributors (2021) es
“Un lenguaje de programación ligero, interpretado, o compilado justo-a-tiempo (just-in-time) con funciones de primera clase. Si bien es más conocido como un lenguaje de scripting (secuencias de comandos) para páginas web, y es usado en muchos entornos fuera del navegador, tal como Node.js, Apache CouchDB y Adobe Acrobat. JavaScript es un lenguaje de programación basada en prototipos, multiparadigma, de un solo hilo, dinámico, con soporte para programación orientada a objetos, imperativa y declarativa (por ejemplo programación funcional).”
Al desarrollar los métodos numéricos en JavaScript los lectores tendrán la oportunidad de ejecutarlos directamente en su navegador sin tener necesidad de instalar ningún otro programa, también podrán editar el código fuente utilizando un editor de texto como bloc de notas o notepad++.
Si bien los métodos numéricos utilizados en este artículo están implementados en el lenguaje JavaScript para la visualización de los resultados directamente en el navegador fue necesario el uso del lenguaje HTML (Hypertext Markup Language) el cual permite desarrollar páginas web.
DIFERENCIACIÓN NUMÉRICA
Partiendo de la noción de derivada como pendiente de la recta tangente a una curva, es decir, su sentido geométrico se pueden deducir procedimientos matemáticos que permiten aproximar el valor de dicha derivada en un punto dado.
Según Anton, Biven y Davis (2010)
La función f’ definida por la fórmula:

Recibe el nombre de derivada de f con respecto a x. Al resolver este límite se puede obtener el valor exacto de la derivada.
Sin embargo, muchas veces a efectos prácticos basta con obtener un valor aproximado, por ejemplo al tomar valores de h cercanos a cero se puede usar la siguiente fórmula para aproximar la derivada de una función de una variable

Esta fórmula se conoce como la fórmula progresiva para la primera derivada, se asumen los dos puntos x0+h y x0 para calcular una aproximación a la derivada, también podrían asumirse los dos puntos cercanos x0 y x0-h en este caso se obtiene

Esta expresión se conoce como la fórmula regresiva para la primera derivada, ambas fórmulas tienen cierto margen de error, para minimizar este error se suele calcular el promedio entre ambas fórmulas
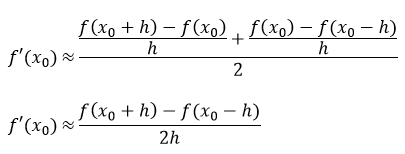
La cual se conoce como la fórmula centrada para la primera derivada, utilizando un razonamiento similar se puede calcular una fórmula que permita aproximar la segunda derivada, se deriva ambos lados de la expresión anterior obteniendo

Ahora teniendo en cuenta que las dos expresiones en el numerador pueden aproximarse utilizando la fórmula centrada para la primera derivada se obtiene

Sustituyendo h*=2h

Por razones de simplicidad se coloca directamente h en lugar de h* debido a que lo importante es recordar que h representa un incremento que tiende a cero, obteniéndose la siguiente expresión

Esta fórmula permite calcular una aproximación al valor de la segunda derivada en un punto de una función de una variable.
CASO DE ESTUDIO: CÁLCULO DE LA VELOCIDAD Y ACELERACIÓN DE UNA PARTICULA EN MOVIMIENTO
Supongamos que la posición de una partícula en el tiempo en un marco de referencia específico está dada por una función de la forma:

Esta expresión describe la posición de la partícula en cada instante de tiempo t, si quisiéramos abordar el problema de la velocidad de la partícula debemos considerar que la velocidad se corresponde con la razón de cambio de la posición en relación al tiempo, es decir, con el concepto de derivada, obtenemos entonces la siguiente ecuación

Aplicando el mismo razonamiento al concepto de aceleración, consideramos que la aceleración es equivalente a la razón de cambio de la velocidad en el tiempo es decir

Ejemplo: Supongamos que una partícula se mueve en un marco de referencia y su ecuación de posición viene dada por

Calcule su velocidad y aceleración para t=7
Hallamos la primera derivada para calcular la velocidad

Luego

Hallamos la segunda derivada para calcular su aceleración

Luego

Estos son los resultados analíticos para la velocidad y aceleración, ahora aplicaremos métodos numéricos para encontrar dichas magnitudes para lo cual usaremos el siguiente código:
<html>
<head>
<link rel='stylesheet' type='text/css' href='plantilla.css'/>
</head>
<script>
x=7;
h=0.01;
vv1derivada=175;
vv2derivada=46;
fx=funcion(x);
fxh=funcion(x+h);
fxmenosh=funcion(x-h);
dif2p=(fxh-fx)/h;
dif2patras=(fx-fxmenosh)/h;
dif3pcentrada=(fxh-fxmenosh)/(2h);
dif3pcentrada2da=(fxh-2fx+fxmenosh)/(h*h);
document.write("<BR/><BR/><BR/><TABLE border=1>")
document.write("<TR><TH colspan=3>DIFERENCIACIÓN NUMÉRICA</TH></TR>")
document.write("<TR><TH>FÓRMULA APLICADA</TH><TH>APROXIMACIÓN</TH><TH>ERROR</TH></TR>");
document.write("<TR><TD>Hacia adelante de 2 puntos</TD><TD>"+redondeo(dif2p,8)+"</TD><TD>"+redondeo(Math.abs((dif2p-vv1derivada)/vv1derivada)*100,4)+"%</TD></TR>");
document.write("<TR><TD>Hacia atras de 2 puntos</TD><TD>"+redondeo(dif2patras,8)+"</TD><TD>"+redondeo(Math.abs((dif2patras-vv1derivada)/vv1derivada)*100,4)+"%</TD></TR>");
document.write("<TR><TD>Centrada de 3 puntos</TD><TD>"+redondeo(dif3pcentrada,8)+"</TD><TD>"+redondeo(Math.abs((dif3pcentrada-vv1derivada)/vv1derivada)*100,4)+"%</TD></TR>");
document.write("<TR><TD>Centrada de 3 puntos (2° Derivada)</TD><TD>"+redondeo(dif3pcentrada2da,8)+"</TD><TD>"+redondeo(Math.abs((dif3pcentrada2da-vv2derivada)/vv2derivada)*100,4)+"%</TD></TR>");
document.write("</TABLE>")
function funcion(x)
{
return Math.pow(x,3)+2*Math.pow(x,2)+4;
}
function redondeo(numero,cifras)
{
var medida=Math.pow(10,cifras);
var resultado = Math.round(numero*medida)/medida;
return resultado;
}
</script>
</html>
Obtenemos los siguientes resultados:

Tabla N° 1 - Resultados obtenidos del Script de Diferenciación Numérica
Se observa un pequeño error (0,13%) al calcular la velocidad mediante la fórmula de dos puntos hacia adelante o hacia atrás para la primera derivada, sin embargo, al utilizar la formula centrada (la cual es más adecuada) el error se reduce casi a cero y para el cálculo de la aceleración mediante la segunda derivada el error es de 0%, estos hechos nos muestran la gran precisión de las técnicas de diferenciación numérica utilizadas en este caso.
En artículos posteriores estaré abordando la implementación de otros métodos numéricos en el lenguaje JavaScript en los cuales los conceptos desarrollados en este artículo serán de especial relevancia.
REFERENCIAS BIBLIOGRÁFICAS Y ELECTRÓNICAS
Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editoria Limusa Willey.
González (2018) Método de las Diferencias Finitas aplicado a la Ecuación Diferencial en Derivadas Parciales de Laplace como solución a un problema de Potencial Electrostático Disponible en el siguiente enlace.
MDN Contributors (2021) Javascript disponible en el siguiente enlace.
Sauer (2013), Análisis Numérico. 2da edición Editorial Pearson.
Has sido votado por
PROYECTO ENLACE
'Conectando Ideas y Comunidades'
PROYECTO ENLACE es un proyecto de curación de habla hispana enfocado en recompensar contenido de calidad y apoyar autores en su proceso de crecimiento en HIVE.
Creemos y apostamos por el futuro de esta gran plataforma, y estamos muy emocionados de poder hacerla crecer junto a esta comunidad. Así que te invitamos a usar nuestra etiqueta ENLACE y estar atento a todas las actividades que tenemos preparadas y que estaremos publicando en breve.
¿QUIERES AUTOMATIZAR TUS GANANCIAS DE CURACIÓN? SE PARTE DEL PROYECTO ENLACE APOYANDO A NUESTRO TRAIL EN HIVE.VOTE INGRESA AQUÍ PARA CONCOCER LOS DETALLES.
¿QUIERES INVERTIR ENLACE? DESCUBRE COMO HACERLO Y GENERAR INGRESOS DE FORMA SEMANAL MEDIANTE TU DELEGACIÓN DE HP AQUÍ TE EXPLICAMOS COMO.
Te invitamos a participar en nuestro servidor de Discord: https://discord.gg/3S9y7BbWfS
Atentamente
EQUIPO ENLACE 2021
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.