Introduction
안녕하세요. @kjs105 입니다. 개강 전 에너지 충전(?)을 위해 푹 쉬느라 글을 쓰지 못했네요.
주말 내내 무기력했는데 이제 공부를 다시 시작하고 글도 가볍게 써보려고 합니다.
저번 시간에는 집합 S와 그 위에 정의된 equivalence relation ~ 으로 quotient set S/~ 를 정의 했었습니다. 이번 시간에는 제가 알고있는 중요한 예시 몇가지에 대해서 알아보려고 합니다.
1. ℚ: the set of rational numbers
우리는 유리수에 대해서 잘 알고 있습니다. 하지만, 수학적으로 어떻게 엄밀히 정의하는지는 잘 모를거에요. 수학적으로 엄밀히 정의하려고 시도를 해봅시다.
집합 X 를 다음과 같이 정의하겠습니다:
X :=ℤ×(ℤ∖{0})
다시 말해서, 첫번째 좌표는 정수이고 두번째 좌표는 0 이 아닌 정수인 모든 순서쌍들의 집합으로 X 를 정의해요.
(눈치가 빠르신 분들은 첫번째 좌표가 유리수의 분자에 해당하고 두번째 좌표가 분모에 해당한다는 걸 아셨을 겁니다)
그리고 relation ~ on X 를 다음과 같이 정의합니다:
(a,b)~(c,d) if and only if ad=bc
(ad=bc 라는 조건은 주어진 두 유리수 a/b, c/d 가 같을 조건임을 알 수 있죠)
그러면 이렇게 정의된 ~는 X 위에서 equivalence relation이 됩니다 (쉬운 연습문제이니 직접 체크해 보세요).
그러면 유리수의 집합 ℚ를 quotient set을 이용해 다음과 같이 정의할 수 있어요:
ℚ:=X/~
사실 X/~ 는 equivalence classes 들의 집합인데, [(a,b)] 를 a/b로 쓰기로 약속하면 우리가 익숙하게 알고 있는 유리수가 되죠.
예시를 들어볼게요. 1 곱하기 4 = 2 곱하기 2 입니다, 따라서 (1,2)~(2,4)가 되고, [(1,2)]=[(2,4)] 입니다. 결론은 1/2=2/4 죠.
사실, 이 예시는 나중에 배울 ring of fraction의 특별한 경우입니다. 그리고 X/~ 는 set보다 추가 구조가 더 주어진 Field 이죠. 이 부분은 나중에 또 다루도록 합시다.
2. ℝ: the set of real numbers
저번에도 말씀드렸다시피 모든 실수의 집합 ℝ을 quotient set을 이용해서 만들 수 있었습니다:
Recall
집합 S 를 다음과 같이 정의하겠습니다:
S := the set of Cauchy sequence in ℚ
(Cauchy sequence는 다들 아시죠? 모르시면 구글링...)
그리고 relation ~ on S 를 다음과 같이 정의합니다:
{a_n}~{b_n} if and only if lim a_n=lim b_n
다시 말해서, 두 수열의 극한값이 같다면 같은 것으로 보자는 얘기죠.
그러면 ~는 equivalence relation on S 가 됩니다 (마찬가지로 체크해 보세요)
마찬가지로 실수의 집합 ℝ를 quotient를 이용해 다음과 같이 정의합니다:
ℝ:=S/~
1번 경우와 마찬가지로 ℝ은 Field가 됩니다.
Remark
1번과 2번 예시는 ℤ 로 부터 ℚ를 만들고 ℚ 로 부터 ℝ을 만드는 과정을 보여 줍니다. 꼭 숙지하세요.
3. G/H: quotient group
대수학에서 중요한 개념인 quotient group은 group 을 subgroup으로 정의되는 equivalence relation 으로 quotient 해서 정의 할 수 있습니다.
이 예시는 제가 Group Theory 를 전개하면서 다시 다룰게요. 지금은 아무래도 equivalence relation과 quotient set을 알아보는 시간이니까... 아무튼 지금 미리 복선을 깔아둘 정도로 중요한 개념입니다.
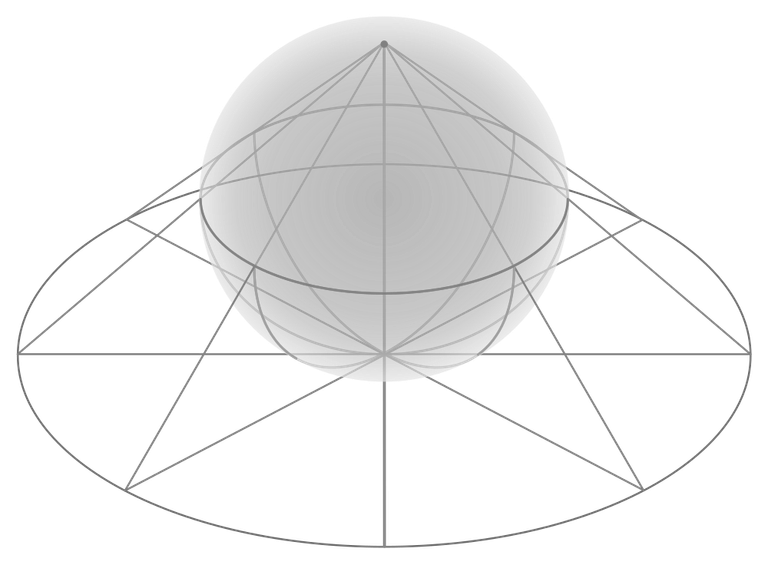
4. ℙ^n(k): Projective space
이번에는 흥미를 위해 기하학에서 예시를 가져와 보겠습니다. (field 를 모르신다면, 사칙연산이 자유롭게 되는 집합을 생각하세요. 예를 들어서 ℚ,ℝ,ℂ 같은 것들.)
일단은 k의 (n+1)-th Cartesian product k^(n+1) 를 생각하겠습니다. (감이 안오신다면, 익숙한 3차원 공간을 생각하세요.)
그리고 여기에서 원점을 뺀 집합 k^(n+1)∖{(0,0,···,0)} 위에서 relation ~ 을 다음과 같이 정의할게요:
(a_0,a_1,···,a_n)~(b_0,b_1,···,b_n) if and only if (a_0,a_1,···,a_n)=(cb_0,cb_1,···,cb_n) for c∈k∖{0}
그러면 ~는 k^(n+1)∖{(0,0,···,0)} 위에서 equivalence relation이 됩니다 (이건 정말 쉬우니 한번 체크해 보세요).
수학적으로 써놓으니 잘 안보일수도 있는데, 직관적인 정의를 말씀드리면, k^(n+1) 위에서 원점을 지나는 직선 위에 원점이 아닌 두 점들이 있으면 그 두 점들을 같다고 하는 겁니다.
예를 들어, k=ℝ 인 경우를 생각해 보겠습니다. 정의에 따라서 (0,1,2)~(0,1/2,1) 입니다, 그리고 (0,1,2)~(0,1/2,1)는 3차원 공간 상에서 한 직선 위에 있죠. (그 직선이 뭘까요? 직선의 방정식은 고등학교 수학에서 배우셨을거에요)
위에 정의한 것들을 이용하여자연수 n과 field k 에 대하여 Projective space (사영공간) 이라는 공간을 다음과 같이 정의할 수 있습니다:
ℙ^n(k):=(k^(n+1)∖{(0,0,···,0)})/~
쉽게 말해서, 사영공간 ℙ^n(k)는 n+1차원 공간에서 원점을 지나는 모든 직선들의 집합이라고 할 수 있습니다.
(출처: Wikimedia)
사영공간은 고전적인 대수기하학에서 많이 쓰이는 object 이며 다들 알아두시면 좋을 것 같아 한번 써보았습니다.
글을 마치며
보시다시피 Quotient 는 수학에서 굉장히 많이 쓰이는 개념입니다. 애초에 quotient 라는 것이 어떤 기준에 대하여 원소들을 분류하는 것을 수학적으로 엄밀히 쓴거라서 거창하고 어려운 개념은 아니지만 굉장히 기초적이고 중요하므로 알아두시면 좋습니다.
오늘은 이만 포스팅을 마치고 다음 시간에 Group theory로 다시 돌아오겠습니다. 감사합니다.
어.. 어렵습니다. 수;;학
응원해주셔서 감사합니다.
어렵지만 기초공사 1층부터 쌓아간다면 누구나 할 수 있습니다 ㅎㅎ 수학의 매력이지요. (1층부터 1000층까지 지어야 할 수도 있지만..)
수학은 너무어려워요! 개강하시면 우수한성적을 기대하겠습니다.
3월의 시작을 아름답게 보내세요^^
그리고 진정한 스팀KR 에어드롭!
[골든티켓x짱짱맨x워니프레임] 9차 옴팡이 이모티콘 증정 천명 이벤트! 그 첫번째 250명 !
https://steemkr.com/kr/@goldenticket/x-x-9-250
아 수학이네요.
저를 팔로우해주셔서 찾아왔는데...
너무 어려우니 이제 찾아오지 말까요?
그래도 종종 수학말고 재미 있는 이야기도 올려 주세요.
일단 읽기는 하지만, 뭐가 뭔 말인지 도통 알 수가 없군요.
유리수를 엄밀히 정의하는 것, 좋은 것이죠.
이것만 알았으면 됐어요.
Hello @kjs105, upv0t3
This is a free service for new steemit users, to support them and motivate them to continue generating valuable content for the community.
<3 This is a heart, or an ice cream, you choose.
:)
R4ND0M:
3304 1237 3606 1161
9564 2294 9543 9029
8189 8785 5508 8825
1249 3623 4004 6796
Congratulations @kjs105! You received a personal award!
Click here to view your Board
Congratulations @kjs105! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!