
[1]
술 취한 새는 둥지로 돌아올 수 있을까? - 고차원에서의 무작위 행보 이론 (Random Walk)
지난 포스팅 수학이야기 #5-1 에서는 1차원 (수직선) 상의 원점에서 시작하여 무작위 행보를 하는 물체에 대해 다루어보았다. 그러나 우리가 사는 3차원 세상에서의 술에 취한 사람은 땅 위를 걸어다니므로, 2차원 상의 무작위 행보로 보는 것이 타당하다. 따라서 이번 포스팅에서는 
1. 고차원 상 Random Walk의 수학적 모델링
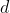
)
)
초기 좌표:
단계 이후의 좌표를
이라 놓으면, 다음과 같은 도식에 따라
이 결정됨을 알 수 있다.
예를 들어서 

지난 포스팅의 Section 2에서 다루었듯이 우리가 관심있는 점들은 \&space;(n&space;>0))
성질 1. 
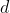



&space;=&space;n)
이고

이므로



성질 2. 두 개의 변수
)
)
를 정의하자. 즉, 





이 성립함을 알 수 있다. 편의상 
2. 생성함수 (Generating Function) 을 이용하여 분석하기 - [2]
2-1. 귀찮은 계산들...
1차원 에서의 경우와 마찬가지로 성질 2에서의 수열 관계식을 풀려면 생성함수를 이용하는 것이 가장 편리하다.

그리고

로 재정의한 뒤, 각각의 생성함수
&space;=&space;\sum_{m=0}^{\infty}&space;\tilde{u}_m^d&space;x^m,\&space;\tilde{F}^d(x)&space;=&space;\sum_{m=0}^{\infty}&space;\tilde{f}_m^dx^m)
를 살펴보면
&space;&=&space;1&space;+&space;\sum_{m=1}^{\infty}&space;\tilde{u}_m^d&space;x^m&space;\\&space;&=&space;1&space;+&space;\sum_{m=1}^{\infty}&space;u_{2m}^d&space;x^m&space;\\&space;&=&space;1&space;+&space;\sum_{m=1}^{\infty}&space;(u_{2m}^d&space;f_0^d&space;+&space;...&space;+&space;u_0^d&space;f_{2m}^d&space;)x^m&space;\\&space;&=&space;1&space;+&space;\sum_{m=1}^{\infty}&space;(\tilde{u}_m^d&space;\tilde{f}_0^d&space;+&space;...&space;+&space;\tilde{u}_0^d&space;\tilde{f}_m^d)&space;x^m\\&space;&=&space;1&space;+&space;\left(&space;\sum_{m=0}^{\infty}&space;\tilde{u}_m^d&space;x^m&space;\right&space;)&space;\left(&space;\sum_{m=0}^{\infty}&space;\tilde{f}_m^d&space;x^m&space;\right)\\&space;&=&space;1&space;+&space;\tilde{F}^d(x)\tilde{U}^d(x)&space;\end{align*})
임을 알 수 있다.
2-2. 문제상황을 대입시키기.
술에 취한 사람이 집으로 돌아오는 것은 다시말하면, 모든 짝수 



이는 다시 쓰면, 생성함수의 극한
)
을 조사하는 것과 동치이다. 앞서 구한 등식을 대입하여 보면,
&space;=&space;\lim_{x&space;\rightarrow&space;1^-}&space;\frac{\tilde{U}^d(x)&space;-&space;1}{\tilde{U}^d(x)})
이므로, 우리는 다음의 극한,
&space;=&space;\sum_{m=1}^{\infty}&space;u_{2m}^d)
만을 조사하면 된다.
3. 결과
3-1. 1차원
지난 번 포스팅에서, 

임을 보였다. 이 때에는 직접 )
3-2. 2차원
이제 
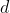




를 만족하고
!}{x_1!y_1!x_2!y_2!})
가지의 서로 다른 경로의 수가 존재하므로 총 경로의 수는
!}{x_1!y_1!x_2!y_2!}&space;&=&space;\sum_{x_1&space;+&space;x_2&space;=&space;m}&space;\frac{(2m)!}{x_1!x_1!x_2!x_2!}&space;\\&space;&=&space;\sum_{x_1&space;=&space;0}^{m}&space;\frac{(2m)!}{x_1!(m-x_1)!x_1!(m-x_1)!}\\&space;&=&space;\sum_{x_1&space;=&space;0}^{m}&space;\frac{(2m)!}{m!m!}&space;\left(&space;\frac{m!}{x_1!&space;(m-x_1)!}&space;\right&space;)^2&space;\\&space;&=&space;\sum_{x_1=&space;0}^{m}&space;{2m&space;\choose&space;m}&space;{m&space;\choose&space;x_1}^2&space;\\&space;&=&space;{2m&space;\choose&space;m}&space;\sum_{x_1&space;=&space;0}^{m}&space;{m&space;\choose&space;x_1}^2&space;\\&space;&=&space;{2m&space;\choose&space;m}^2&space;\end{align*})
가 나온다. 마지막 등식은 이항정리의 성질로 부터 유도됐다. 따라서,

를 만족함을 알 수 있다. )
&space;=&space;\infty)
)

이 성립하고, 따라서
&space;=&space;\sum_{m=0}^{\infty}&space;u_{2m}^2&space;&=&space;\sum_{m=0}^{N-1}u_{2m}^2&space;+&space;\sum_{m&space;=&space;N}^{\infty}&space;u_{2m}^2&space;\\&space;&\geq&space;\sum_{m=0}^{N-1}u_{2m}^2&space;+&space;\frac{K^2}{\pi}&space;\sum_{m=N}^{\infty}&space;\frac{1}{m}&space;>&space;\infty&space;\end{align*})
이 성립한다. 즉
2차원의 경우에도, 무작위 행보는 언제간 반드시 돌아옴을 알 수 있다.
3-3. 3차원 - [3]
이제 마지막으로 3차원을 살펴보자. 물론 인간은 날아다닐 수 없으므로, 3차원에서의 무작위 행보는 사람에게 해당되지 않는다. 적절한 예시를 찾아보면, 날아다니는 새 정도? 를 들 수 있다. 그럼 과연
술에 취한 새는 무작위 비행 중 언젠가 둥지로 돌아올 수 있을까?
이에 대한 답을 하기 위해서는 
위와 똑같은 방법으로 구해보면, 다음을 얻는다
^{-2m}&space;{2m&space;\choose&space;m}&space;\sum_{x_1&space;+&space;x_2&space;+&space;x_3&space;=&space;m}&space;\left(&space;\frac{m!}{x_1!x_2!x_3!}&space;\right&space;)^2)
다항정리에 의해
^2&space;=1)
이므로
^2&space;\leq&space;\max_{x_1,x_2,&space;x_3}&space;\frac{m!}{x_1!x_2!x_3!})
가 성립한다.
다항정리의 계수가 최대가 되려면, 모든 

!(m/3)!(m/3)!}&space;\\&space;&\sim&space;\frac{1}{\sqrt{\pi&space;m}}&space;3^{-m}&space;\frac{\sqrt{2\pi&space;m}(m/e)^m}{\prod_{i=1}^3&space;\sqrt{2\pi&space;m/3}&space;(m/3e)^{m/3}}&space;\\&space;&\sim&space;K&space;\frac{m^{m-1/2}}{m^{1/2&space;+&space;3/2&space;+&space;m}}&space;=&space;K/m^{3/2}&space;\end{align*})
이고 
&space;=&space;\sum_{m=0}^{\infty}&space;u_{2m}^3)
술에 취한 새는 무작위 비행 중 언젠가는 둥지로 돌아온다고 확정지을 수 없다.
3-4. 3차원 이상의 고차원
사실, 위의 식에서 

!(m/d)!...(m/d)!}&space;\\&space;&\sim&space;\frac{1}{\sqrt{\pi&space;m}}&space;d^{-m}&space;\frac{\sqrt{2\pi&space;m}(m/e)^m}{\prod_{i=1}^d&space;\sqrt{2\pi&space;m/d}&space;(m/de)^{m/d}}&space;\\&space;&\sim&space;K&space;\frac{m^{m+1/2}}{m^{1/2&space;+&space;d/2&space;+&space;m}}&space;=&space;K/n^{d/2}&space;\end{align*})
가 된다. 

&space;=&space;\sum_{m=0}^{\infty}&space;u_{2m}^d)
따라서 3차원 이상의 Random Walk는 반드시 회귀를 보장하지는 않는다.
4. 예시
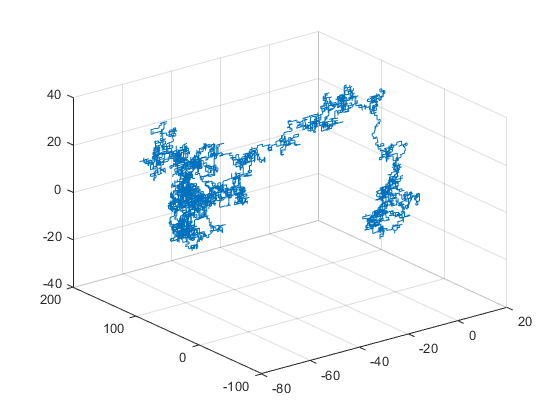
MATLAB을 이용하여 2, 3차원 Random walk를 나타내보면 다음과 같다.
%% 2D & 3D Random Walk
M = 10000;
X = [0 0 0]';
p = [1/6 1/6 1/6 1/6 1/6 1/6];
for i = 2 : 1 : M+1
x = randsample([1 2 3 4 5 6], 1, true, p);
if x == 1
X = [X, X(:,i-1) + [1 0 0]'];
elseif x == 2
X = [X, X(:,i-1) + [-1 0 0]'];
elseif x == 3
X = [X, X(:,i-1) + [0 1 0]'];
elseif x == 4
X = [X, X(:,i-1) + [0 -1 0]'];
elseif x == 5
X = [X, X(:,i-1) + [0 0 1]'];
else
X = [X, X(:,i-1) + [0 0 -1]'];
end
end
plot(X(1, :), X(2,:));
grid on;
figure;
plot3(X(1,:), X(2,:), X(3,:));
grid on;
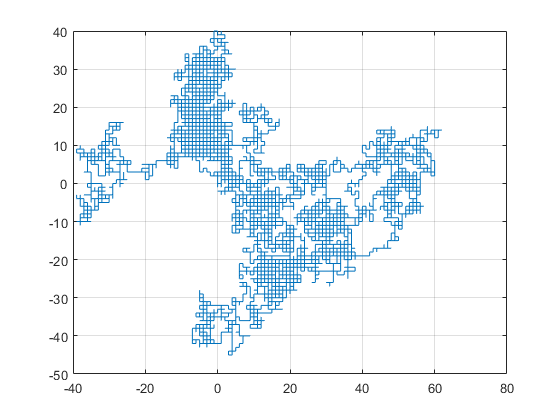
5. 결론
1차원 (수직선) 과 2차원 (좌표평면)에서 무작위 행보 운동을 하는 물체는 언젠가는 시작점 (원점)으로 회귀한다.
3차원 이상에서의 무작위 행보는 회귀를 담보할 수 없다
술에 취한 사람은 집에 돌아오지만 술에 취한 새는 둥지로 돌아가지 못할 수 있다.
6. 출처/인용
[2] https://www.dartmouth.edu/~chance/teaching_aids/books_articles/probability_book/Chapter12.pdf
[3] https://services.math.duke.edu/~rtd/PTE/PTE4_1.pdf
7. 추신
다음 이야기 부터는 좀 더 쉽고 재밌는 주제로 써보겠습니다.
)
골 때리는데 재밌네요ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ 막연히 고차원에서도 까짓거 언젠가 돌아오겠지 생각했는데, d ≥ 3 에서 u2m가 수렴하는군요. 어쩐지 새가 좀 더 지구 자기장을 잘 느끼고 방향을 잘 찾는다 했더니, 수학적인 이유가 있었네요ㅎㅎㅎ
읽어주셔서 감사합니다 !
확실한 컨셉이 있으시네요ㅋㅋㅋ 여행 다녀오시기 전 @beoped님도 이렇게 수식이 난무하는 포스팅을 종종 하셨는데, 자주 찾아뵙겠습니다.
와우! 제가 등장했군요! 여행 후 요새는 다시 우주에 빠져 있어서 ㅋㅋㅋ
수학 포스팅도 한번 준비해 봐야겠군요;;
@mathsolver 님 금융 수학 포스팅도 종종 올려주세요! ㅎㅎ [쉽고 재미있는 주제는 아니네요;; ㅋㅋㅋㅋ] 예전에 한참 블랙숄즈모형 같은거 PDE 풀고 모델링하고 했었는데.. Financial Engineering 보고 떠올랐네요 ㅎㅎ
이오스 계정이 없다면 마나마인에서 만든 계정생성툴을 사용해보는건 어떨까요?
https://steemit.com/kr/@virus707/2uepul