
저축을 시작하고 처음 1억 원을 모으는 데까지는 좀 시간이 걸리지만, 이 문턱을 넘어서고 나면, 복리의 마법이 발휘되기 시작하면서, 순 자산은 점점 더 빠르게 증가하기 시작한다.
이 글에서는 순 자산이 1억 원 문턱을 넘은 후 로켓처럼 이륙하기 시작하는지 간단한 수학으로 살펴보도록 한다.
수학
가상의 직장인 성실이가 매년 1천만 원을 저축해 투자한다고 해보자. 연평균 수익률 7%를 적용하면, 7.84년 후에 순 자산이 1억 원까지 성장한다.
※ 원 글의 달러를 원으로 바꿨다. 1달러를 1천 원으로 단순화했다.
※ 연평균 7% 수익률이 터무니없다는 댓글이 달릴지 모르겠다. 예시를 위한 것일 뿐이니 그냥 넘어가 주시고, 개념만 기억하시기 바란다. 아래 표에 연평균 수익률 3%에서부터 다양한 사례를 담아놓았다.
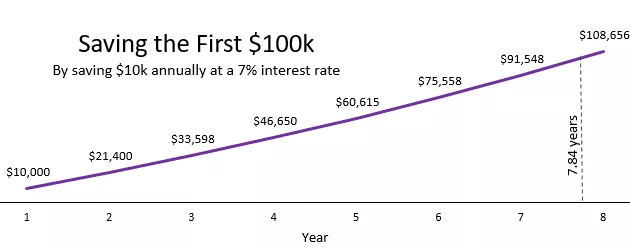
성실이가 계속해서 매년 1천만 원을 저축해 연평균 7% 수익률로 투자한다면, 다음 1억 원까지는 5.1년이 걸리게 된다.

시간이 흐를수록, 성실이가 1억 원을 늘리는 기간이 점점 더 짧아진다.
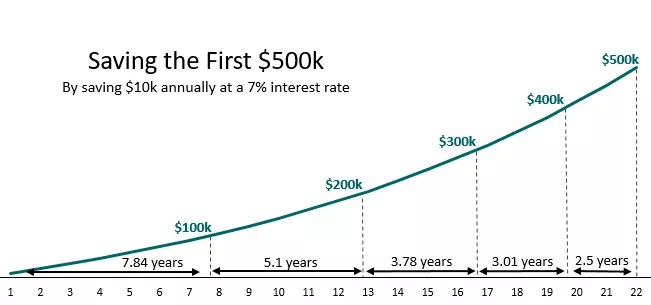
성실이가 매년 똑같은 액수를 저축하지만, 이미 저축한 돈이 알게 모르게 일을 하고 있기 때문에, 순 자산은 매년 더 빠른 속도로 자라나는 것이다.
다음 차트는 다양한 연평균 수익률에 따라 매 1억 원이 추가되는 기간을 보여준다(한도 20억 원까지):

성실이가 연평균 7% 수익률로 꾸준히 매년 1천만 원을 저축하고 투자해 나간다면, 놀라운 결과가 나온다. 순 자산을 0원에서 1억 원으로 키우기까지는 7.84년이 걸린다. 하지만 순 자산을 6억 원에서 10억 원으로 키우는 데는 6.37년 밖에 걸리지 않는다.

즉, 일단 1억 원을 모으고 나면, 복리의 마법이 얼마나 강력하게 발휘되는지 잘 보여주는 대목이다. 찰리 멍거가 말했듯이, 처음 1억 원을 모으기가 어렵지, 일단 그 문턱을 넘고 나면, 이 돈이 무거운 짐을 대신 들어주기 시작한다.
위 차트에서 주목할 점은 첫 1억 원을 만들기까지는 연평균 수익률이 3%~9% 중 어느 경우라도, 7~8년이 걸린다는 점이다. 왜냐하면 저축을 시작한 초기에는 투자 수익률보다 저축 금액 자체가 훨씬 더 중요하기 때문이다.
추가로, 다음 차트는 다양한 연간 저축액에 따라 1억 원을 모으는데 걸리는 기간을 보여준다. 이 차트는 연평균 수익률 7%를 기준으로 했다.
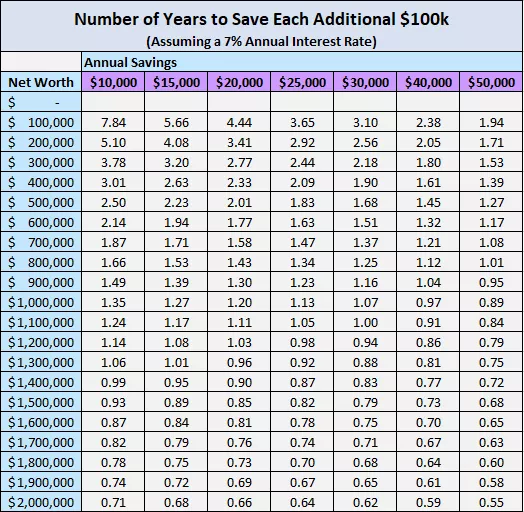
모든 경우에 같은 수학이 적용된다.
연간 1천만 원을 연평균 7% 수익률로 저축하고 투자하는 시나리오는 복리의 마법을 설명하기 위한 가상일 뿐이다. 하지만 이 수학은 모든 저축액과 수익률에 공히 적용된다. 시간이 흐를수록, 순 자산은 복리의 마법으로 매년 점점 더 빠르게 증가하게 된다.
유감스럽게도, 복리의 마법은 순 자산이 1억 원 문턱을 넘어가기 전까지는 자신을 드러내지 않는 경향이 있다. 수익률의 영향이 눈에 띄게 되는 시점은 순 자산이 충분해질 때부터다.
여기서 배워야 할 중요한 교훈이 있다. 처음 1억 원을 모으기 위해 바라던 것보다 더 오랜 기간이 걸리더라도 결코 낙담하지 말라는 것이다. 어쩌면 상징적으로 1억 원이 달성하기 가장 어렵고, 가장 오래 기간이 걸리는 걸린다.
여기서 우리의 성실이의 연봉 상승은 전혀 감안하지 않았다. 경력이 쌓일수록, 연봉이 높아질 가능성이 높고, 더 많은 액수를 저축할 수 있게 된다. 이렇게 저축 액수가 많아지면, 복리의 마법은 더 빠르게, 더 강하게 작용할 것이다.
자료 출처: Four Pillar Freedom, "The Math That Explains Why Net Worth Goes Crazy After the First $100k"
수익율 7프로 유지가 참 어려운데...
Posted using Partiko iOS
저는 언제쯤 1억원을 모을 수 있을런지...
기념비적인 글이네요.
우리나라에도 이에 필적할만한, 통장으로 하는 자산 불리기 방법이 있는데 잘 기억이 안 나네요.
"위 차트에서 주목할 점은 첫 1억 원을 만들기까지는 연평균 수익률이 3%~9% 중 어느 경우라도, 7~8년이 걸린다는 점이다.
왜냐하면 저축을 시작한 초기에는 투자 수익률보다 저축 금액 자체가 훨씬 더 중요하기 때문이다."