안녕하세요, 오랜만에 돌아온 @yey입니다! 이 주제에 대한 글을 쓰기 시작하고 나서 어떻게 이어가야 할 지 고민하느라 글 작성이 늦어진 것 같네요. 이번 글에서는 (많은 분들은 이미 아시겠지만) 왜 정다면체가 다섯 가지 밖에 존재하지 않는지 그 이유를 적어보고, 다음 글에서는 4차원에서는 어떻게 여섯 가지의 정다포체가 존재하는지, 그 다음 글에서는 5차원 이상에서는 왜 정다면체에 해당하는 도형이 세 종류 밖에 없는지 다뤄보겠습니다.
Hello, it's been a long time! This is @yey. It took a long time for me to start writing this post, because, after I started to write about this topic, I've been considering about what would be a good topic to write about in the following posts. In this post, I'll explain about why there are only five regular polyhedra (even though I guess most of you already know the reason), and then in the following posts, about why there are only six regular polytopes in 4-dimensional space and why there are only three such things in each space of dimension greater than or equal to 5.
이 글 전체에서 다면체는 유한하고, 볼록하고, 구멍이 없는 다면체로만 제한하겠습니다.
Throughout this post, a polyhedron means only a bounded, convex polyhedron with no holes inside.

정다면체 찾기 Finding Regular Polyhedra
3차원 유클리드 공간에서 정다면체를 찾기 위해서는 먼저 다음과 같은 조건들이 아주 유용합니다.
The conditions in the below are very useful to find all the regular polyhedra in the 3-dimensional Euclidean space.
- 모든 다면체는 다음 공식을 만족한다. All polyhedra satisfy the following formula: v-e+f=2
- 다면체의 각 꼭짓점에서는 세 개 이상의 같은 개수의 면이 만난다. Each vertex of a polyhedron is shared by at least three faces.
- 다면체의 각 꼭짓점에서 만나는 면들의 그 점에서의 내각의 합은 360 ° 를 넘을 수 없다. For each vertex of a polyhedron, the sum of all internal angles that meet at the vertex cannot exceed 360 °.
조건 2와 3에서 한 면이 정사면체인 정다면체는 각 꼭짓점에서 세 개, 네 개, 또는 다섯 개의 면이 만나야만 하고, 한 면이 정사각형이거나 정오각형인 정다면체는 각 꼭짓점에서 세 개의 면이 만나야 한다는 사실과 정다면체의 한 면은 여섯 개 이상의 변을 가질 수 없다는 걸 알 수가 있습니다.
By the conditions 2 and 3, we see that if a regular polyhedron is composed of equilateral triangles, then three, four, or five faces can meet at each vertex, if a regular polyhedron is composed of squares or regular pentagons, then exactly three faces meet at each vertex, and that there is no regular polyhedron composed of a regular polygon with more than five edges.
이제 정다면체의 한 면이 정n각형이고, 한 꼭짓점에서 p개의 면이 만난다고 해보겠습니다. 위에서 말한 대로 가능한 순서쌍 (n, p)는 (3, 3), (3, 4), (3, 5), (4, 3), (5, 3)이 전부입니다. 이제 각각의 경우에서 어떤 정다면체가 만들어지는지, 정다면체의 꼭짓점의 수(v), 모서리의 수(e), 면의 수(f)는 어떻게 되는지 알아보겠습니다.
Suppose that a regular polyhedron is composed of regular n-gons and p faces meet at each vertex. As I mentioned above, the only possible pairs for (n, p) are (3, 3), (3, 4), (3, 5), (4, 3), and (5, 3). Now I will show you what regular polyhedron we can get in each case and how many vertices(v), edges(e), and faces(f) it has.
정다면체의 f개의 면에 각각 n개의 점이 있고, p개의 면이 한 점을 공유하므로 정다면체의 꼭짓점의 개수는 (nf/p)가 됩니다. 또, f개의 면에 각각 n개의 변이 있고, 2개의 면이 한 모서리를 공유하므로 정다면체의 모서리의 개수는 (nf/2)가 됩니다. (v=nf/p, e=nf/2)
Our regular polyhedron have f faces with n vertices, and p faces meet at each vertex. So the number of vertices of this regular polyhedron is (nf/p). Also, it have f faces with n edges, and 2 faces meet at each edge. So the number of edges of this regular polyhedron is (nf/2). (v=nf/p, e=nf/2)
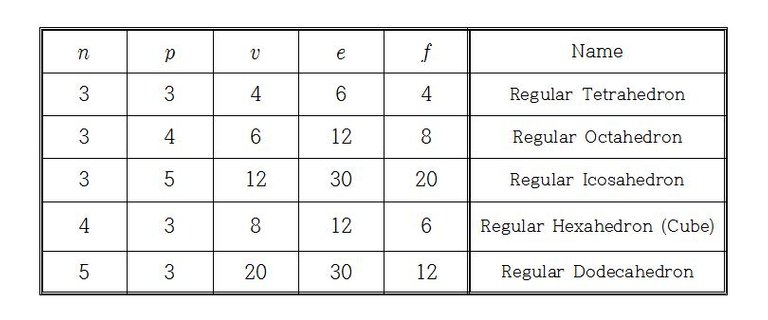
이제 조건 1에 의해 식 v-e+f=(nf/p)-(nf/2)+f=2를 얻고, (n, p) = (3, 3), (3, 4), (3, 5), (4, 3), (5, 3)를 대입해주면 각각의 경우에 f=4, 8, 20, 6, 12를 얻고 각각의 경우에서 v와 e값도 찾아주면 아래와 같은 정다면체의 완벽한 분류표를 얻게 됩니다!
By the condition 1 above, we have v-e+f=(nf/p)-(nf/2)+f=2, and by substitution (n, p) = (3, 3), (3, 4), (3, 5), (4, 3), (5, 3), we have f=4, 8, 20, 6, 12 for each case. We can also find the values of v and e for each case and we finally get the whole list of regular polyhedra below!
The Schläfli symbol
마지막으로 Schläfli symbol에 대해 언급하고 이번 포스트를 마칠게요. 위에서 보였듯이 (n, p)만 가지고도 하나의 정다면체를 특징 지을 수 있는데 그래서 정다면체를 {n, p} 라는 기호를 이용해서 나타내기도 하고 이걸 Schläfli symbol라고 해요. 예를 들면 정십이면체는 Schläfli symbol이 {5, 3}인거죠. 마찬가지로 4차원에서는 정다면체들이 모여 정다포체를 만들어내는데 정다면체 {n, p}가 한 모서리에 q개 모여서 정다포체를 이루면 Schläfli symbol이 {n, p, q}가 됩니다. 다음 포스트에서는 말씀드린대로 4차원 공간의 6개 정다포체를 찾는 법에 대해 다루도록 하겠습니다! 읽어주셔서 감사합니다 :)
Before finishing this post, I'll just introduce the Schläfli symbol. As we shown above, we could specify a regular polyhedron with the pair (n, p), so we just express a regular polyhedron as {n, p} called the Schläfli symbol. For instance, the Schläfli symbol for regular dodecahedron is {5, 3}. Similarly, a 4-dimensional regular polytope is composed of regular polyhedra. If it is composed of {n, p}, and q regular polyhedra meet at each edge, we express this 4-dimensional polytope as {n, p, q}. As I said above, in the next post, I will explain about how to find all the six 4-dimensional polytopes! Thank you for reading :)
그나저나 스팀잇에 편하게 수식을 입력할 방법이 없을까요?
By the way, is there any easy way in Steemit to type mathematical formula?
전 사실 텍으로 작업한 것들을 캡쳐해서 그림판으로 올리는데... tex format 이 없다면
링크 에서 수식 입력후 이미지 형식으로 옮겨 쓰셔도 됩니다.
아 그렇게 하시는 군요 ㅎㅎ 근데 스팀잇 자체가 사진 올리는 것도 좀 불편해서 여러모로 번거롭게 하네요 ㅋㅋ
Schläfli symbol 은 예전에 KMS 잡지였나 에서 한번 보고 지나간 적이 있었는데.. 대학교 같은 곳에도 정규 수업으로 거의 안 다루는 내용이라 앞으로도 관련 내용 많이 기대하겠습니다. ㅎㅎ
작년에 교보문고에서 '다면체' 란 책을 보긴 했는데 저랑 많이 생소해서 이해를 거의 하지 못했었죠... 이어지는 포스팅들을 통해서 책의 내용을 조금이라도 이해할 수 있으면 좋겠네요 ㅎㅎ
사실 저는 <Regular Polytopes (Coxeter 지음)>라는 책을 살까 고민 중입니다! 아직 오목한 모양(별 모양) 다면체나 정다면체 말고도 다른 종류의 중요한 다면체들 등등 알아야 할 게 너무 많아서 걱정이네요 ㅋㅋ 아직 하나씩 알아가는 단계지만 열심히 글 작성해보도록 할게요 :)
전 그래서 직접 손으로 쓰는 경우가 많은것 같아요 수학관련 글 많이 올려주세요^^
아 @yurizard님은 직접 손으로 쓰시고 찍어서 사진으로 올리시는군요! 감사합니다~
Congratulations @yey! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP