Hello steemians, it's been a very busy two weeks for me. It was midterm week, which meant creating and grading midterms; then we were sponsoring a Math Olympiad, which meant organizing some 80-odd elementary, middle, and high school students on a bright and sunny afternoon. All in all, it was a hectic yet somehow energizing experience.

Anyways, one of my students recently asked a question which frequently comes up every time I introduce the concept of matrices and vectors for the first time: "Why does the determinant of a matrix give the area of the parallelogram enclosed by its vectors?"
The technical answer is because det(A) represents the area or volume magnification factor for the linear the particular linear transformation given by the matrix.
To understand this a bit better, we should have a clear understanding of what is meant by a linear transformation. In this context, a linear transformation on a vector takes place when we multiply a matrix by a vector, which is to say something like:
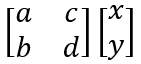
Now the rules of linear transformation essentially state the following:
- All straight lines must stay straight lines.
- The distance between lines can change, but they must be evenly spaced after the transformation.
In practice this means essentially that, if you were to draw a coordinate grid, you are allowed to stretch and skew the grid, but not bend the paper, nor move the origin. For example, this would be linear transformation:

While something like this would not be:
In any case, let's consider the general case above. If we multiply the matrix by the vector we get:
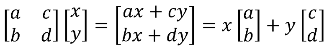
Which essentially means that for any vector, you're transforming the x coordinate by multiplying it by the vector [a, b]T and the y coordinate by multiplying it by the vector [c, d]T. In other words, it takes the unit vectors and changes them to [a, b]T and [c, d]T, and because linearity is preserved, it simply means that any vector [x, y], is simply a linear combination of the two vectors transformed unit vectors.
A few special cases
In R2 we call a matrix a rotation matrix if it can be expressed as:

This rotates every point about the origin by θ degrees. For instance, if I have a square with vertices at (0,0), (1,0), (1,1) and (0,1), to get the transformed square, I multiply:
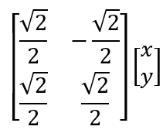
Replacing the vector [x, y]T with the desired points. The result looks like this:
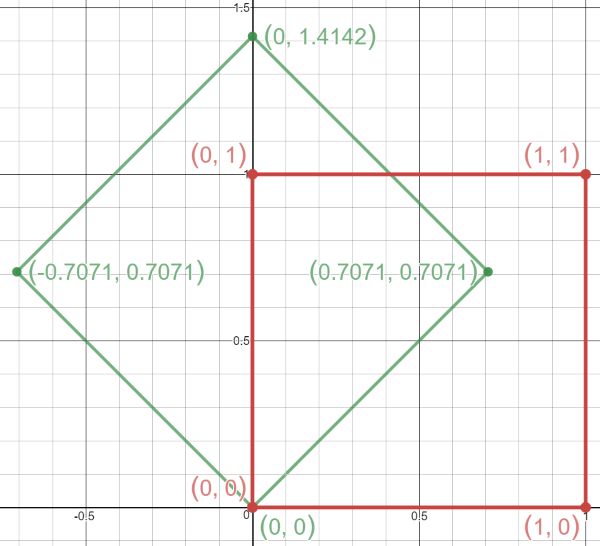
One can easily verify, using coordinate geometry that the green figure is a square of side length 1. Since this is a rotation, it does not change the area of the square, it merely rotates it 45 degrees around the origin.
Next, we'll investigate a matrix with a values only along the diagonals, of the form: 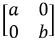 .
.
In this case, it is obvious that a square will be stretched out into a rectangle with vertices at (0,0), (a, 0), (a, b) and (b, 0). Therefore, the area of the square will now be ab where previously, it was 1.
Back to determinants
So, back to our original question: "Why does the determinant of a matrix give the area of the parallelogram enclosed by its vectors?".
In this case, any matrix A might represent all of those things that we're doing to the square. Therefore, any given matrix A (does it have to be square?), might in fact be the net result of multiplying several matrices together to get the desired result. In other words, If A is a 2 x 2 matrix with column vectors a and b, then the linearity means that A transforms the unit square in R2 into some parallelogram in R2, for instance:"
In practice, we could imagine that we could repeatedly stretch, skew, and rotate a square, performing several operations successively to obtain a desired parallelogram. In this case, any square matrix A would represent the net result of each individual operation. In other words, if we successively multiply several square matrices together, we would get the coordinates for the vertices of that parallelogram. Graphically, that matrix multiplication would look something like this:
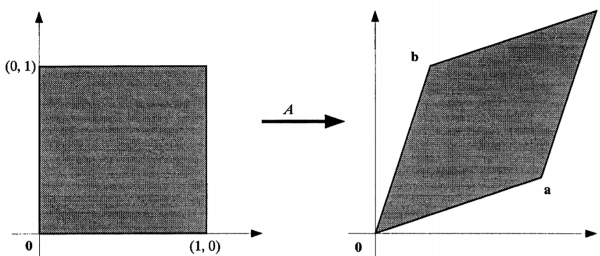
In this case, the vector (0,1) has been changed to (a,b) and the vector (1,0) has been changed to (c,d). Now, we can re-arrange the parallelogram to look like this without changing the area, thus transforming it into a rectangle:
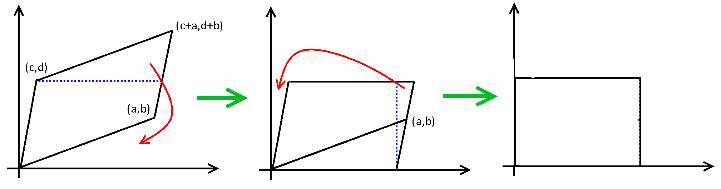
It should be obvious that the height of the rectangle is d, and that its width is 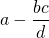 . Multiplying this product, we get that:
. Multiplying this product, we get that: 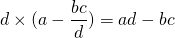
This is precisely the textbook definition of the determinant of a two-by-two matrix. The same logic can naturally be applied for a three-by-three matrix. In this case, the determinant would yield the volume of the parallelopiped enclosed by the three column vectors of that matrix.
Further Remarks
There remain a few things to be said: Firstly, what happens if the determinant is negative? This is of course possible should if $bc$ > $ad$. Well, a negative determinant essentially means that the orientation of the axes relative to one another has changed. In our normal coordinate system, the $y$ axis is found in the counterclockwise direction relative to the $x$ axis, but it is possible to change this orientation by "mirroring" the coordinate system. In essence, the area is still scaled by the absoute value of the determinant, but if one imagines that the square is drawn on a glass window, it simply means you're viewing the same drawing from the other side of the glass.
Secondly, what happens when the determinant is zero? It will turn out that both column vectors comprising the square matrix are in fact linearly dependent, because ad = bc. For instance, if the matrix is 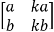 , then the determinant is zero, and therefore the area of the parallelogram will be zero. This means that either all vectors will collapse onto a single line, or onto a single point.
, then the determinant is zero, and therefore the area of the parallelogram will be zero. This means that either all vectors will collapse onto a single line, or onto a single point.
Concluding Remarks
Here, we've seen that the determinant of a two-by-two matrix gives the area of a parallelogram enclosed by its two vectors. In fact, we can generalize this to three dimensions, in which you would obtain the volume of the solid (called a parallelopiped), as well as higher dimensions. We saw that this is achieved essentially because a unit square is transformed into the said parallelogram, and that geometrically, the area turns out to be precisely the determinant.
Content type: long, educational




Awarded 4 out of 6 owls:
Details: The originality owl is only awarded if the post explains the math in a creative/novel way. The citation and sources owl was not awarded since it needs to be explicitely if the images are original. Also, a source for further reading is much appreciated.
Hey write more math posts :D