What are you sitting on? Is it a chair? Now tell me why it is a chair? If you are sitting on something, why isn't it called a star? Why isn't your mother = father?
You can give me some answers that sound like I'm questioning something that is obvious. After all 2 isn't 1 and 2+2 isn't 5 and you'd say those things are obvious. then let me ask you why those things are obvious? Why is "A" called "A"?
Time To Talk About Infinity & Beyond (Which Is Also Infinity - Sort of)
Numbers are just concepts to begin with. By the time you count that there is 1 apple, you already have 2 things. You have the "1" and then you have the "apple" that correspond to the said "1". Not a single natural number stands alone as something real. You can neve show me a number. you can show me a symbol, that represent the number like: 183621581 But those digits are merely representing a number.
A Simple Idea From physicsforums.com
I always wondered, how can any number raised to the power of 0 be 1. So, I came up with this! ( * = multiplication sign)
1 * 4 * 4 * 4 = 4^3
1* 4 * 4 = 4^2
1 * 4 = 4^1
Therefore, 1 = 4^0
Now we could go on to say that x^0 = 1
Then we can say (x+1)^0 = 1
Without going far we could simply replace x with any natural number and say x^0 = 1
Which would lead to something like 1=2=3=4=5=173635292= Googleplex
It sounds madness but it's middle school math.
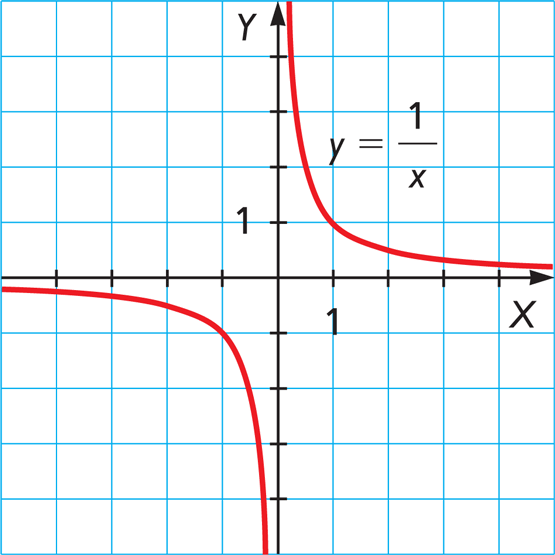
Division By Zero
This one is actually officially "Undefined " in mathematics. Here is what the Wikipedia is saying:
- In various branches of mathematics, certain concepts are introduced as primitive notions; for example, in geometry these might be given the names "point", "line", and "angle". As these terms are not defined in terms of other concepts, such terms may be called "undefined terms".
-A function is said to be "undefined" at points not in its domain – for example, in the real number system, {\displaystyle f(x)={\sqrt {x}}} f(x)={\sqrt {x}} is undefined for negative {\displaystyle x} x, i.e., function {\displaystyle f} f assigns no value to negative arguments.
-As a special case of the latter, some arithmetic operations may not assign a meaning to certain values of its operands, such as happens with division by zero. In such a case an expression involving such an operation is called "undefined".
Additionally Wikipedia Says:

Basically it all comes down to this sort of a cop out that says you can't divide by zero. You have to state this or else 0.000234 will be equal to 343495833.8932183
Treating Zero As A Concept; Not A Number
There can be an infinity that is infinitely bigger than the infinity. There can be an infinity that is twice as big as the infinity (1,2,3,4,5........ Vs 2,4,6,8,10,12.........) It's all just a concept. There is an infinite amount of rational numbers between 2 consecutive integers. when we count 1,2,3,4,5...... one could say that we are counting infinities. Infinity isn't a static number. Isn't it the same for zero? If there is nothing to be counted to begin with, how can you say that it is a single unchanging digit?
Although infinity and zero happens to be the numbers that are furthest apart (when negative numbers are left out) they have so many things similar to them almost like 2 sides of a coin. Numbers are concepts. Zero and infinity are a whole new kind of concepts.

We make up terms like "unicorns" that describe something unreal...so infinity either is a unicorn or if real...has to be something we can point to...makes we wonder...is the universe without borders....having no edge therefore "infinite"?
It's an informative post and helpful to the ones inclined to mathematics. Keep up the good work :)