I'm going to start a maths degree at Oxford next week and I thought a good project for the year would be to write about an interesting bit of maths that I had found that week.
How to go about answering such a question?
Before we talk about the line and the square, we'll consider a different question. Are there more numbers between 0 and 1 or between 0 and 100? At first it seems obvious, and there is a seemingly fool proof argument: Suppose there are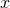 
numbers between 0 and 1, between 0 and 100 there must be 
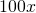numbers. Hence there are more numbers between 0 and 100, since 100 > 1. This is a flawed argument, and to explain why we'll need to introduce the idea of sets.
A bit of set theory
A set is just a collection of things - usually numbers. For example the set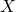 
could be assigned like so: 
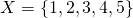- just a set of the first 5 integers. This is an example of a finite set. Sets can be finite or infinite, with an example of an infinite set being the natural numbers: 
. The fancy N is the standard notation for the set of natural numbers.
All sets have other sets associated with them called subsets. A subset is a set that contains some (or all) of the members of another set. A proper subset is a subset containing strictly fewer members of another set. Eg: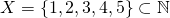 
with the 
symbol meaning 'is a subset of.' Here all the elements of X are natural numbers, and it has fewer elements so it is a proper subset of the natural numbers.
A key property of infinite sets (which finite sets don't possess) is that there exists a one to one mapping from at least one proper subset to the set its self. This is almost the formalisation of the idea that infinity + 1 = infinity. For example, consider the set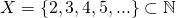 
and the set 
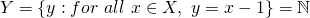. Since the set Y is a mapping from X which is a proper subset of the natural numbers, and Y is the natural numbers, this shows that there are infinitely many natural numbers.
Going back to the discussion of the number of numbers, the sets we are dealing with are infinite so there is no finite value of 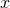that we can assign, so it isn't clear that 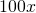> 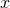. Also, with our new found knowledge of sets we could show that there exists a mapping from 
to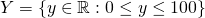 
namely 
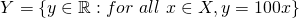and hence there are the same number of numbers between 0 and 1 as there are between 0 and 100. If you claim otherwise, then consider the fact that it is impossible to pick a number between 0 and 100 that doesn't have an associated number between 0 and 1. For all the numbers you pick, you will never run out of numbers between 0 and 1. (Here the fancy R is the set of all real numbers, so think fractions and irrational numbers. A rigours definition of the real numbers is perhaps a topic for another post.) An exercise for you to try would be to find a mapping from the interval 0 to 1 to the entire real numbers - to show that the total number of numbers is the same as the number of numbers between 0 and 1.
Back to the line and the Square
I'll use sets to define exactly what we mean. The line could be the set of numbers and the square could be the set of points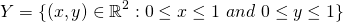 
. And the question is, does there exist a mapping from X to Y? Let's first have a look at possible mappings. One is
which actually ends up being part of the unit circle. The problem with this is that there is a cyclicity to this set - after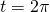 
the trigonometric functions just output the same numbers. The next logical thing to try would be 
but this still has the same problem and will do for all rational coefficients. This is because for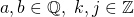 
where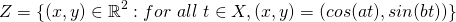 
, it can be shown that there is a solution to this pair of simultaneous equations: 
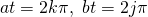. However, if one chooses irrational coefficients to define the points like this: 
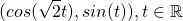(multiplying the coefficients or applying some function to t can get around the fact that t is now an unbounded real number) then you can prove that there exists no solution to the previous simultaneous equation.
The proof
Suppose that for there exists a solution to these simultaneous equations: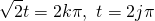 
where k and j are integers. Then, dividing the first equation by the second equation we get 
which is false since the left hand side is irrational where as the right hand side is rational. This means that there is no t such that at the same time such that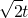 
and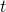 
are both multiples of 
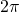and hence the trigonometric functions in the point 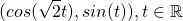are always out of phase. Therefore the set 
is a mapping from [0, 1] to the square of side length 2 centred at the origin. So there are the same number of points on a line as there are in a square - the set is of the same size.
Conclusion
I think this went off the rails a bit in terms of mathematical complexity - it was difficult to write the end bit in a beginner friendly tone - feel free to ask any questions. But hopefully the idea of one to one mappings representing the number of numbers is interesting and beneficial to you.
Very interesting post. It's always funny how math can go against the obvious reasonings in your brain :)
For me it's always difficult to accept some of the rules. My logical mind says there are more numbers between 0 and 100 than between 0 and 1. After all 1 is between 0 and 100 but 100 is not between 0 and 1.
I'm not sure if I'm making sense but I did quite some math at university and it was always hard for me to shut down my obvious logic brain :)
Yeah, I like the bits of maths that go against your intuition, and you can't really explain it thinking about numbers and amounts as you usually do. Thanks for reading!
Best of luck with studying at Oxford! I completed my engineering and math degree at the University of Queensland.
Nice, are you now working in education or is steemit more of a hobby?
Mate, I'd love to do this education and steemit as a full time gig, and I'm trying to work towards it. Engineering was surprisingly an unstable career choice in Australia, so I'm actually now nearly completed a Physiotherapy degree at the same University. Maths, engineering and teaching in those areas is till my passion, so I'll definitely continue on this path even if it's part time. :)
Physiotherapy is an interesting choice! I had this idea for a site a while back when I was still trying to figure out what I wanted to do which would be a collection of resources (videos and books etc) that would guide you towards increasing your understanding of particular subjects. So I would have this problem where I could read any number of popular physics or science books but never really get to the sort of pre undergrad level that I needed to see what the subject was really about. Everything online was either way to advanced, I already thought I knew the content or I didn't think I needed to know a seemingly unrelated bit of maths for something in physics. Say you went to the site and wanted to learn more about Quantum Mechanics, then the site would say you need to know all this linear algebra and calculus and give you good resources for those topics. If you're interested, I'd quite like collaborate to start compiling a list for different topics around maths, physics and engineering to see whether the site is viable.
Sounds like a great idea. I'm definitely open to it. Short term commitment may be a challenge at the moment because I have some final end of semester exams coming up. Also, I'm still new to Steemit, so I'm not sure yet about the best way to communicate on a more personal level.
What you're describing is sort of what I'm trying to achieve with my videos (primarily on YouTube). It's been an on and off labor of love for the past 4 years. I'd love to have something eventually as big as Khan Academy, but more specialised for Engineering.
I love the idea of progressive content. So with my current videos on DE's, I started at the basics and eventually want to cover the entire spectrum, up to where it's applied in dynamics, heat equations and structural analysis.
I did mathematics at Cambridge until O levels. Then I went into Medicine. So now you clearly understand that I don't understand you. Your question confuses me. There are infinite points on any structure depending on what you call a point. The same concept as measuring a coastline. Am I wrong? Or just perfectly right ?
Yeah, the idea of number of points it's a bit badly defined - what I really mean is the size of the set, so since there is a one to one mapping from each point on a line to a point in a square the size of both sets is the same, but the interesting thing is that the line is contained in the square
This may be your last warning.
Get out of Mathematics. !
Honestly I am jealous. I have achieved much in life more than I expected, but math is language of the Gods. The is not much to this universe but beautiful math. From Pi to Golden ratio and everything in between.
Good luck with all your endeavors.
Fantastic write up - I am not well-versed in mathematics but you did a good job at explaining these concepts in layman's terms. You will likely do well at Oxford. Best of luck in all that you aspire to be!
Thanks mate, Did well to read it in two minutes ;)
When it comes to facts and objective statements I do pretty well, lol
I always thought a point had a position but an infinitesimal size and a line segment had a way to specify the segment (start/end positions or other) but an infinitesimal width. Either way, that means there's an infinite number of points on a line segment and an infinite number of points (and line segments) in a square.
Yeah, but there are different sizes of infinities - for example there isn't a 1 to 1 mapping from the integers to the real numbers, so there are more real numbers than integers - however there is a 1 to 1 mapping from the integers to the rational numbers, so there are the same number of integers as there are fractions. The question is really is the infinity of points that makes up the square larger than the infinity of points that makes up the line. Thanks for reading!
Yes. I realise that and it is helpful to think about different sizes of infinities. My favourite example that is easier to grok is the comparison between the set of natural numbers and the set of even numbers. That's like thinking from the inside - it works by looking at the members of the set. From the outside of the set infinite is infinite and since infinite is not a quantity then the set sizes are not comparable. Right now though I think we're talking about some finer points of theory that don't particularly matter outside of any particular application.
So, yes, we can use the intuition that although the number of points on a line segment are infinite, and the number of line segments in a square are also infinite, there are more points in a square. By extension the number of squares in a cube is infinite.... that leads to the number of points in shapes of various dimensions:
1D: inf (e.g. points on a line segment)
2D: inf^inf (points on a square)
3D: inf^inf^inf (points in a cube)
4D: inf^inf^inf^inf (points in a 4D hypercube)
etc....
If your definition is more restrictive for how the shapes go into the higher dimensions, such as it must be an exact slice of the higher dimensional shape and they must be packed without overlaps, then the density chnges somewhat. First what do I mean by an exact, non-overlapping slice, a row of points on a line segement. Then a row (or column) of equal length line segments that extend from edge to edge of the square... (extend into higher dimensions). Then the density of points increases proportional to the number of dimensions:
1D: inf
2D: inf^2
3D: inf^3
4D: inf^4
This is fun stuff btw :)
One of the main points about what I was writing was sort of to get across how unintuitive it is. The set I wrote at the end sort of generalises to higher dimensions so if you let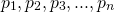
be the first n prime numers just to avoid factors and perfect squares and consider the set
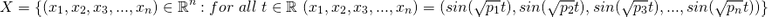
then you have lots of functions going between -1 and 1 that are always out of phase as proved above with the irrational number bit, so they will produce every combination of n numbers between -1 and 1 and hence cover any n dimensional square/cube/ whatever you call it in higher dimensions. This is a mapping from the real numbers to that square. If you can't read the maths then try downloading the image
Good post. Which college are you going to?
BTW the mathematics looks well-formatted; did you just type in Latex? I requested native latex support a couple of months ago, but didn't hear back if it had been implemented. Thanks.
Thanks - upvoted. You may be interested in joining a project dedicated to helping quality authors further: Minnows Accelerator Project.
Join over 150 like-minded quality content creators. And please upvote this comment so that we can continue to support the best new content creators. Thanks!
Thanks mate and Univ. All the maths was formatted on http://quicklatex.com which just generates a png. I'm not sure whether this is basically the same output as if latex was supported properly or whether it would be written in real text.
OK, that's how we're all doing it - latex into images; just that yours looks well-formatted inline.
Resteemed.
Congratulations @homes! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @homes! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @homes! You have received a personal award!
Click on the badge to view your own Board of Honor on SteemitBoard.