There is less than a week until Selection Sunday when the group of 68 teams is finalized for this year's NCAA Division I college basketball championship. Which means I only have a few more sets of games to test out models as I attempt to fill out a perfect bracket. Granted I expect to have all of my brackets broken within the first four games, but for now, the dream remains alive for 2019.
Last time, we augmented the SPM and introduced some more information into the model by using the margin of victory and sigmoid functions to give different weights to different games based on how large the margin between both teams was. Today, we'll augment our original model (EDM) and use a different approach to looking at predicting games in order to maximize our odds of catching perfection in a bottle.
So far, I have created three different models and have implemented a reference model that all do the same sort of thing. They generate some metric based on information that we feed into the model. Using that metric, we pick teams based on the value of that metric. The team will the highest value for the metric is predicted to win the respective tournament they are participating in.
But this approach assumes that any path to the final is irrelevant as long as your team is the strongest team on that path. But what if we looked at this from a probability standpoint? A team might have the best score, but given a harder path, we should expect it to lose to a team with a worse score, but a much easier path. The NCAA tournament is seeded which makes this scenario a lot less likely than if the tournament was randomly drawn, but seeding is not perfect (of course) so the difficulty of a team's path should definitely be taken into consideration.
So, we have the Estimated Difference Metric. For those unfamiliar, feel free to read up on the model here. The EDM rating is simply a score. For our purposes, we need to calculate or estimate the "odds" of winning a game given an opponent's EDM rating.
We could generate distributions for these teams and calculate probabilities for these, but given the low sample size and the fact that most of the tournament teams will be facing teams at the upper edge of their sample set, the information that we might obtain from these distributions has a good chance at not being too accurate.
A better approach is to estimate a win likelihood from a team's entire schedule and then weighting those samples by how similar they are to the opponent in question. So, we will add the results of the games (0 or 1), weight them by distance in EDM rating, and then take the weighted average to get an estimated win probability for a team at that specific EDM rating, even when a team doesn't have a large number of samples of comparable teams.
This method generates a likelihood using the results of other games, weighting them using EDM as a proximity (distance) measure in order to create an average "expected" likelihood at the specific EDM (the next opponent) in question. We'll take this model one step further and use the sigmoid function we used for the previous model in order to generate fuzzy numbers between 0 and 1 to differentiate between dominant wins and narrow ones.
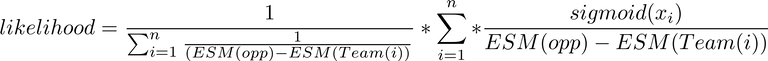
This final equation which calculates the likelihood which can then be normalized against the other likelihood (the opponent against the current team) to create two probabilities which add up to one. We can then assign these probabilities and multiply them along with other probabilities on the bracket to select a "most likely" winner rather than just using the team with the best EDM score.
While the math is kind of complicated to try and give an example with the formula, let's go over the general idea with an example to give you an idea of why this model differs from the others. Let's say we have four teams each with different likelihoods of winning their first and second games. Team A is facing Team B and Team C is facing Team D. The probabilities are made up, but are definitely in the realm of possibility given this scenario.
| Team | Probability of Winning First Match | EDM Rating |
|---|---|---|
| A | 0.51 | 1947 |
| B | 0.49 | 1941 |
| C | 0.91 | 1887 |
| D | 0.09 | 0728 |
Team A is the best team of the four and they are expected to win their first game narrowly since Team B is only a few points away from them in EDM Rating. Team C is the third best team, but they are expected to win comfortably against Team D who is considerably worse than all three teams. Let's move to the second game, the final of this small tournament.
| Team | Probability of Winning Second Match | EDM Rating |
|---|---|---|
| A | 0.63 | 1947 |
| C | 0.37 | 1887 |
Using a pure EDM model, we would just declare Team A the winner, but let's take a look at each team's prospective path to the championship:
Team A = 0.51 * 0.63 = 0.3213
Team C = 0.91 * 0.37 = 0.3367
The first game for Team A is a toss up while the first game for Team C is a likely win. The odds for Team C to show up in the championship are better than the odds for Team A. The odds are so much better that they make Team C the favorite for the tournament even though they won't be the best team in the championship and will certainly be the underdog in that match up.
It may still be confusing why anyone would pick Team C when Team A or Team B would be favored in the match up, but its due to the fact that you have very little confidence in either Team A or Team B. With individual games, it would make a lot of sense to pick the best or second best team in the tournament, but context and the chain of opponents matters. Games in single elimination tournaments aren't independent, they are entirely dependent on the prior game and the fragility of any one team makes uncommon results like the one shown in the example of something to consider when bracket building.
Now that we have four models to play with, let's see which teams they predict to win another tournament to see whether or not there is consensus or disagreement in the models. Today, we'll check out the MAC tournament which starts today to see which teams are favored to go deep into the tournament.
First off, it should surprise no one that all four models predict Buffalo to win the tournament. The team is ranked Top 20 nationally and has compiled a 28-3 record against some impressive competition as well as dominated the MAC. Our likelihood model (which is fairly conservative) gives Buffalo 77% chance of making the final and greater than 50% to win the whole thing. This means Buffalo is more likely to win than all the other teams combined. Here are the projected Top 5 teams from the other three non-probability based models:
| Seed | Team | EDM Rank | SPM Rank | MASPM Rank |
|---|---|---|---|---|
| 1 | Buffalo | 1 | 1 | 1 |
| 2 | Toledo | 2 | 2 | 2 |
| 3 | Bowling Green | 3 | 4 | 5 |
| 4 | Kent State | 5 | 3 | 3 |
| 5 | Central Michigan | 4 | 5 | 4 |
So there is consensus among the models for the Top 2 teams in the conference with some disagreement with how the rest of the teams round out the Top 5. Kent State and Central Michigan are likely to face in the second round, so we should be able to get good information out of that game.
Below are my projections and results from the conference tourneys so far to this point. Of the four tournaments that have concluded, my models have not been able to get any to this point sadly. In fact, the models have a good reputation of selecting the runners-up in three of cases. But hey, perfection was always an unreachable goal. Hopefully, I'm able to get one perfect bracket for one of the 32 tourneys from these models, or at least at a minimum, pick a winner (I hope).
Projections (So Far):
| Conference | EDM | SPM | MASPM | Actual |
|---|---|---|---|---|
| Atlantic Sun | Liberty | |||
| Big South | Gardner-Webb | |||
| Patriot | Colgate (7-1) | TBD | ||
| Horizon | Northern Kentucky (3-1) | Northern Kentucky (4-0) | TBD | |
| Northeast | Saint Francis (PA) (4-2) | TBD | ||
| Ohio Valley | Murray State | |||
| MAAC | TBD | |||
| Missouri Valley | Bradley | |||
| West Coast | Gonzaga (3-3) | Gonzaga (2-4) | Gonzaga (2-4) | TBD |
| Southern | Wofford (6-2) | Wofford (8-0) | Wofford (8-0) | TBD |
| America East | Vermont (3-1) | Vermont (3-1) | Vermont (3-1) | TBD |
| Colonial | Hofstra (5-1) | Hofstra (4-2) | Hofstra (5-1) | TBD |
| Summit | TBD | |||
| Record | 62-27 | 60-29 | 29-18 | EDM, MASPM lead |
Honestly I don't think it is possible. There are too many variant sand which team turns up on the day. I was a sportsman and sometimes the underdog in matches we as a team would lift our performance. What normally happens when a team has an upset they will have a good run as they have gained confidence but their abilities may be limited and will be found out. It will be good to see if you can get a perfect bracket, but that is unlikely.
Firstly, a calculus post that got upvoted by @curie, what are the odds of that? Can we get a calculation on that? Thanks!~ Secondly, a post that makes a practical application of a theoretical equation and not only as a hook but a means to explain a thing? My oh my, now it just becomes getting juicier each and every second I type this comment out. Thirdly - okay let's cut the joking out now
Now I never really cared for televised sports events (mainly the anchor people that commentate on the event's proceedings) and so I just never paid attention to events. What I did knew of was how people decided to math sports (with good reason) and make sense of trends, which in all honesty should be looked into as this post doesn't make light off (and for good reasons that I appreciate that for). Also I must give gracious thanks for not only collecting a whole sum of data, a reference model but also a set of three different models - time-consuming for sure, thankfully computers can spit out code like the bad-machines they are!~
Also the topic of this post is rather interesting in my eyes, truly. Not because it literally is a prediction model based upon calculus, but more-so the fact of what is being strung together as I continue to look at it. To Calc one me, that would've looked like some hodgepodge of a mess before I realize how messy series can get and the trickery calculus nerds do to get any connection between data points.
The examples seem rather fine, as aforementioned, and seem reasonable - so do scratch the data collected on some part but keep it for the rest. Now I just do wonder if there's a model for models that calculates their range of error over time which then leads into meta analysis... which finally leads to fixing up models or making stronger ones and running the data again all over again. Fun with statistics being backed up by Calculus in the auxiliaries~
Hi statsplit,
Visit curiesteem.com or join the Curie Discord community to learn more.
Congratulations @statsplit! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPVote for @Steemitboard as a witness and get one more award and increased upvotes!