Solution:
The problem of the last contest was:
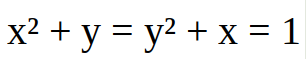
This is basically a system of 2 equations:
1: x² + y = 1
2: x + y² = 1
From 1 we can derive:
3: y = 1-x²
3 in 2:
x+(1-x²)² = 1 | -1
(x-1)+(1-x²)² = 0 → x₁ = 1
x⁴ - 2x² + 1 + x - 1 = 0
x⁴ - 2x² + x = 0 → x₂ = 0
↓
x³ - 2x + 1 = 0 | ÷(x-1). This can be done because x₁ = 1 is an already known 0
x² + x - 1 = 0
→ x₃₋₄ = -½ ± √(¼ + 1) = -½ ± (√5)/2
→ x₃ = -½ + (√5)/2; x₄ = -½ - (√5)/2
Using equation 3 that yields the following 4 solutions:
(1; 0) (0; 1)
(-½ + (√5)/2; -½ + (√5)/2)
(-½ - (√5)/2; -½ - (√5)/2)
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
What is your chance of winning:
p(You Win) = 1/n, n = number of entries
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
List of participants with their entries:
| Name | solutions found | comment |
|---|---|---|
| @golddeck | (0, 1) (1, 0) | |
| @masoom | all four(with rounding errors) | first complete entry → 1 SBI |
| @mmunited | Nothing but a few formulas for x and y | Accepted anyway due to low number of complete entries. |
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Winner draw:

That makes 1 SBI for @masoom and @golddeck:

↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Thanks!
I wonder why so few people are participating (0, 1) (1, 0) were really not super hard to find.
I don't know.
Why didn't you participate then?
I scrolled down too far and saw the answers so I didn't feel like participating anymore because it would have been cheating. But there odds to win here are much better than a lot of the other contest even if you only have half of the solutions. I guess everyone just hates math :D