By this stage of physics, we will have spent a lot of time learning about properties of materials – conductors have resistance, fluids are viscous, and so on. But at very low temperatures we cannot take these properties for granted. At 4 K, for example, mercury loses all its electrical resistance and so can carry a current forever without any reduction in the current. At very low temperatures, helium becomes a fluid that loses its viscosity and can flow freely. Oxygen even becomes magnetic.
Scientists are working to achieve lower and
lower temperatures and trying to discover more unusual low-temperature
properties in a wider range of materials.
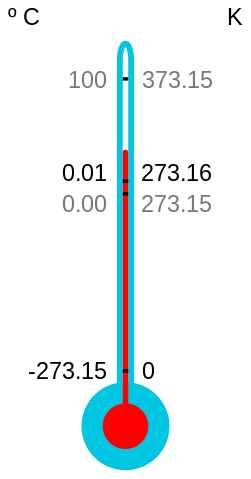
The absolute zero of temperature has been defined as 0 K (about -273.16 °C), when the only remaining energy is ‘zero-point’ energy that arises from the so-called uncertainty principle and can never be removed. We also know that we will never be able to reach absolute zero. But that doesn’t stop scientists from trying to get as close to it as possible.
Eric A. Cornell, Wolfgang Ketterle and Carl E. Wieman of the United States shared the 2001 Nobel Prize for Physics for research that involved cooling a gas down to just above 1 nK (1 billionth of a degree above absolute zero). The technique involved slowing down alkali atoms by colliding photons head-on with them and then skimming off the faster atoms by evaporative cooling to obtain a condensate. But competition continues. At the low-temperature Laboratory in Helsinki, Finland, a piece of rhodium metal has since been cooled to 100 pk (0.1 nk).
The ideas in this chapter
Ever since physicists knew about absolute zero temperature, they have been trying to reach it. This is a problem of thermodynamics, that is, the study of energy transfer processes including work and heating, and how these two processes are connected.
But thermodynamics is a lot more than trying to reach absolute zero. Thermodynamics explains why we can heat and expand a gas to drive internal combustion engines: most vehicles rely on some form of thermodynamic (heat) engine. It explains the limits to transferring energy, and shows, for example, that we can never build a totally efficient power station to supply electricity. In the home, thermodynamics explains the operation of refrigerators and other equipment that we use to do work for us.
THE ZEROTH LAW
When physicists first began to study thermodynamics, they identified three laws. Logically enough, they called these laws the first, second and third laws of thermodynamics. However, in the 1930s they realised that there was a much more fundamental law than these, so, rather than change the names of the others, they called the new one the zeroth law of thermodynamics.
This states: If two bodies are in thermal equilibrium with a third body, then they must be in thermal equilibrium with each other.
If two or more bodies are in this kind of equilibrium, they must have the same temperature because thermal energy is not transferred between bodies that are at the same temperature. For energy to be transferred thermally, a temperature gradient is required. Without the zeroth law a practical thermometer would not be possible.
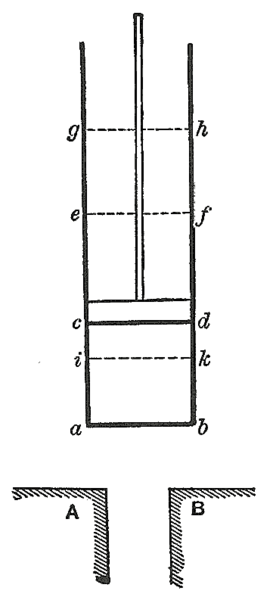
We use the zeroth law in calibrating a thermometer. A practical thermometer (such as a mercury thermometer) and a gas thermometer are both placed in a liquid or similar reservoir of thermal energy. The gas thermometer is an ‘ideal’ thermometer used to define temperature. Both thermometers reach thermal equilibrium with the liquid. Then the two thermometers are also in equilibrium with each other and so they are at the same temperature. This means that the practical thermometer can be calibrated against the gas thermometer for a fixed temperature. Further points can be established by altering the temperature of the liquid as measured using the gas thermometer.

THE FIRST LAW
We saw that Joule found he could increase the temperature of water by doing work on it. He kept the water thermally insulated from the surroundings so that no energy was thermally transmitted to the water from outside. But the internal energy of the water changed. The internal energy is the sum of the potential and kinetic energy of the molecules in the substance. We use the symbol U for internal energy (measured in joules) and represent a small change by ΔU. We assume that a small amount of work ΔW is done to produce this change of internal energy. So the change of internal energy in joules is:
ΔU = ΔW
Alternatively, the internal energy of the water could be increased by allowing energy to enter from the outside, usually by thermal processes (such as conduction). We often call this energy ‘heat’ or ‘thermal energy’. Assume that this amount of energy (in joules) entering the water is small, represented by ΔQ. The change of internal energy is given by:
ΔU = ΔQ
This assumes no work has been done.
But most changes in the internal energy of a body arise from a combination of both thermal transfer and mechanical transfer of energy or work. So more generally, we write:
ΔU = ΔQ + ΔW
We can use any combination of amounts of thermal energy or mechanical energy (work) to produce a given change of internal energy ΔU. The equation is an algebraic statement of the first law of thermodynamics. We can state the law in words: The increase in internal energy of a system is the sum of the work done on the system and the energy supplied thermally to the system.
It is probably easier for us to remember the law as the equation ΔU = ΔQ + ΔW. Notice that in words, the law refers to a system. In our example, the system is the mass of water whose temperature has been raised by work or heating.
Sometimes we need to consider what happens to more than one object: we may have to consider the behaviour of a number of components. We refer to them altogether as our system – we can think of the system as surrounded by an imaginary wall. All things outside this wall are the surroundings. The system plus its surroundings taken together make up its universe.
Although energy can be transformed in different ways, it is not possible to create or destroy energy. Later, I will discuss about how mass can be turned into energy and how energy can be transformed into mass. This is possible only with nuclear interactions; it does not happen in everyday thermodynamics.
APPLYING THE FIRST LAW TO A GAS
Most real-life engines contain a gas which is heated and expands, and the gas (which does the work) follows a cycle of changes before it ends up under the same set of conditions as when it started the cycle. I shall look at the expansion of a gas, and other changes, restricting ourselves to an ideal gas. Because there are no forces of attraction or repulsion between the molecules of an ideal gas, the only way that the internal energy and the temperature of the gas can change is to change the kinetic energy of the molecules. This, in turn, makes an ideal gas system easier to consider than many of other systems.
We look at what happens when work is done by the gas. Let's assume that the gas is inside a cylinder with one of its end closed. And, at the other end is a piston. The molecules travel round inside the cylinder, having a collision with the walls, and rebounding off the walls and piston. This causes a pressure p on the walls and piston. The pressure acts on the piston of area A, producing an overall force:
F = pA
Suppose that, as a result of this force, the piston moves outwards slightly so that the volume of the gas increases. We then make the following assumptions:
- There is neglectable friction between the walls of the cylinder and the piston.
- The force F that is exerted by the gas is balanced by an external force F.
- But the external force will be reduced by a very minute amount.
This very slight imbalance of forces allows the piston to move. We assume it travels a small distance Δx so that there is negligible change of pressure of the gas. The volume of the gas changes by a small amount ΔV. The gas does work ΔW in expanding against the external force. We therefore have:
work = force × distance
ΔW = FΔx = pAΔx
The product AΔx is the increase in volume ΔV of the gas. So the work done by the gas is:
ΔW = pΔV
Note that if we consider the work done on the gas, the equation must have a minus sign:
ΔW = -pΔV
EXAMPLE
A circular piston of diameter 40 mm contains a gas at 3 atmospheres. Calculate the work done by the gas when the piston moves outwards a small distance (compared with the length of the cylinder) of 5 mm. Given that 1 atmosphere = 1.01 × 105 Pa.
Answer: Work done = pressure × change of volume
= pAΔx
= 3 × 1.01 × 105 × [π × (20 × 10-3)2 × 5 × 10-3] J = 1.9 J
ISOTHERMAL CHANGES IN A GAS
When the volume of a sample of gas changes, there is often a change of pressure. A common situation is for a gas to change its volume at constant temperature, that is, under isothermal conditions. Here we can use the equation of state for an ideal gas:
pV = nRT
where R is the gas constant and n is the number of moles in the sample. Experimentally, we can achieve an isothermal change by changing the volume slowly so that the gas remains in thermal equilibrium (that is at the same temperature) with the surroundings. With temperature constant, the pressure is related to volume by:
p = constant/v
This inverse dependence is shown on the pV diagram. To find the work done by the gas when it expands, we plot the curve for actual values of p and V and measure the area under the curve. Remember: work done = pAV. We measure the area by adding up the areas of the large number of strips (each a pΔV) making up the total area. Alternatively, we can obtain a mathematical expression for the work done. This does not require values of p to be calculated.
Calculation of the work done by a gas during an isothermal expansion
For a small change in volume, the work done is given by:
ΔW = pΔV [1]
Also we use the ideal gas equation:
p =nRT/V
Substituting for p from equation 1
We get:
ΔW = nRTΔV/V
Instead of adding strips of width ΔV, we use calculus to integrate dW = nRTdV/V between the initial volume V1 and the final volume V2:
dW = ∫nRTdV/v = nRT∫dV/V
As the integral of dV/V is In V, we obtain:
dW = nRT[ln V] = nRT(In V2 – InV1) = nRT In (V2/V1)
CHANGE OF PRESSURE OF A GAS AT CONSTANT VOLUME
Rather than changing the volume of a gas at constant pressure, we might choose to alter the pressure at constant volume. Suppose the gas is in a container with fixed walls and we change the temperature by either heating or cooling. Because the volume is fixed, the gas equation tells us we can expect the pressure to rise with a temperature increase: the kinetic energy of the gas molecules increases, their momentum increases, they make greater impacts as they collide with the walls, and so pressure on the walls increases.
Although we change the internal energy, no work is done. We can confirm this on the pV diagram where the change is represented by a vertical line: below this line there is no area.
How much energy is required to raise the temperature of the gas by 1 kelvin? The amount will depend on the quantity of gas involved. We usually take one mole of gas and quote the molar heat capacity, which is the amount of energy in Joules required to heat 1 mole by 1 kelvin. The symbol for this is Cv.
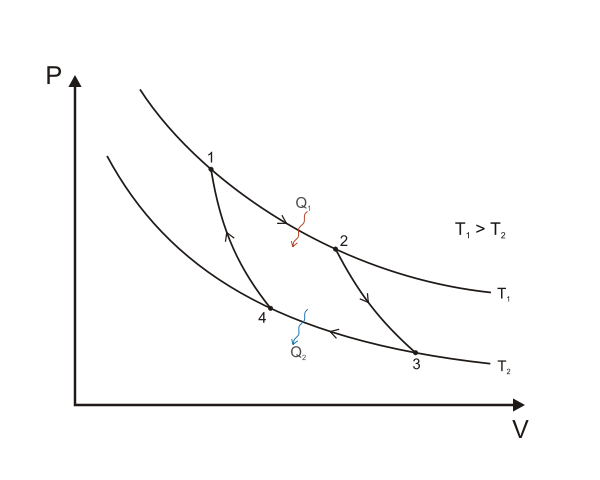
A Carnot cycle illustrated on a PV diagram to illustrate the work done. Keta, CC BY-SA 3.0
The amount of energy needed to increase the temperature of the gas by a small amount ΔT is CvΔT. The subscript V tells us that this is the molar heat capacity at constant volume. No work is done on the gas (it does not change volume). All the thermal energy Qv supplied goes to changing the internal energy of the gas. For 1 mole of gas:
ΔU = ΔQv + CvΔT
CHANGE OF VOLUME OFA GAS AT CONSTANT PRESSURE
We have seen that the work done by an ideal gas in expanding by a small amount ΔV is pΔV. If the expansion is large, the only way in which the pressure can remain constant (from the gas equation) is for the temperature to increase. The pV diagram tells us that work done is still pressure × volume change, as this is the area under the horizontal line representing the change.
Again, we need to be able to work out by how much internal energy is increased. This time, we use the molar heat capacity at constant pressure, Cp. It is defined as the amount of energy in joules required to heat 1 mole of gas by 1 kelvin at constant pressure. For gases, the molar heat capacities at constant pressure and constant volume are not the same. When an ideal gas is heated at constant pressure its volume increases. It must do work against its surroundings as well as increase its internal energy (kinetic energy of the molecules). As a result, we expect the molar heat capacity at constant pressure to be significantly larger than that for constant volume for a gas. For liquids and solids, the difference is very small because they expand very little on heating at constant pressure.
SUMMARY OF MOLAR HEAT CAPACITIES FOR AN IDEAL GAS
Assume that Qv is the thermal energy which is joined to the ideal gas at constant volume, Qp is the thermal energy that is added at constant pressure, and ΔT is the change in temperature in each case. Then, for n moles of the gas:
ΔQv = nCvΔT and ΔQp = nCpΔT
that is:
Cv = ΔQv/nΔT and Cv = ΔQv/nΔT
It can be shown that there is a simple relationship between the two molar heat capacities for an ideal gas: Cp – Cv = R
REFERENCES
https://www.coursehero.com/file/p393hja/The-reference-gas-thermometer-C-is-in-thermal-equilibrium-with-liquid-B/
https://www.livescience.com/29913-coldest-places-on-earth.html
https://en.wikipedia.org/wiki/List_of_weather_records
https://en.wikipedia.org/wiki/Lowest_temperature_recorded_on_Earth
https://www.thoughtco.com/zeroth-law-of-thermodynamics-4177952
https://courses.lumenlearning.com/boundless-physics/chapter/the-zeroth-law-of-thermodynamics/
https://www.livescience.com/50833-zeroth-law-thermodynamics.html
https://en.wikipedia.org/wiki/Zeroth_law_of_thermodynamics
https://www.britannica.com/science/thermodynamics/The-first-law-of-thermodynamics
https://www.livescience.com/50881-first-law-thermodynamics.html
https://en.wikipedia.org/wiki/First_law_of_thermodynamics
http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/isoth.html
https://www.askiitians.com/iit-jee-thermal-physics/work-done-during-isothermal-expansion.html
https://en.wikipedia.org/wiki/Isothermal_process
https://www.youtube.com/watch?v=m9h6qyWLscs
https://www.bbc.co.uk/bitesize/guides/zc4xsbk/revision/3
http://chemistry.bd.psu.edu/jircitano/gases.html
https://www.grc.nasa.gov/www/k-12/Numbers/Math/Mathematical_Thinking/ideal_gases_under_constant.htm
https://en.wikipedia.org/wiki/Gas_laws
@tipu curate
Upvoted 👌 (Mana: 20/30 - need recharge?)
Hello,
Your post has been manually curated by a @stem.curate curator.
We are dedicated to supporting great content, like yours on the STEMGeeks tribe.
Please join us on discord.
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.
Students can now receive electrical engineering assignment help at a very budget cost from Help In Homework. Our team of experts has all the qualifications that are needed to do the job and have profound knowledge about this field. Most of them are pursuing a career in academia or in the corporate world but have decided to help out students with homework and assignments for just a nominal price. Their objective in life is that money is important but what is more important is to strike a balance between work and life. And they have experienced first-hand how difficult it can be to achieve this balance in academic life. Thus, they are offering their services to students of electrical engineering to help them overcome some of the stress from their very busy schedule that requires juggling multiple tasks.