¡Hola amigos de Steemit!


De acuerdo con Terence (1999), “(…) se ha desarrollado un cierto número de ecuaciones más o menos empíricas, de fácil solución, que se usan en problemas de flujos en tuberías”. La fórmula de Hazen-Williams (FHW) viene dada de la siguiente manera:
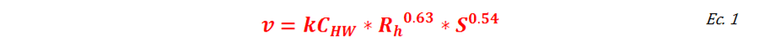

En el Sistema Internacional de Unidades (SI): k = 0,849

Por lo tanto la FHW se expresa de la siguiente manera:

En el Sistema Inglés: k = 1,318

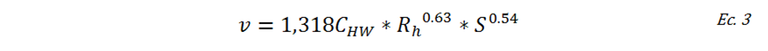
Es decir, la fórmula tal como está expresada permite determinar la velocidad del flujo de agua en una conducción conociendo los tres factores previamente descritos.

López et al. (2003), señalan que “(…) el coeficiente de Hazen-Williams representa la influencia que la rugosidad de la conducción tiene en las pérdidas de carga.” Por lo tanto, 
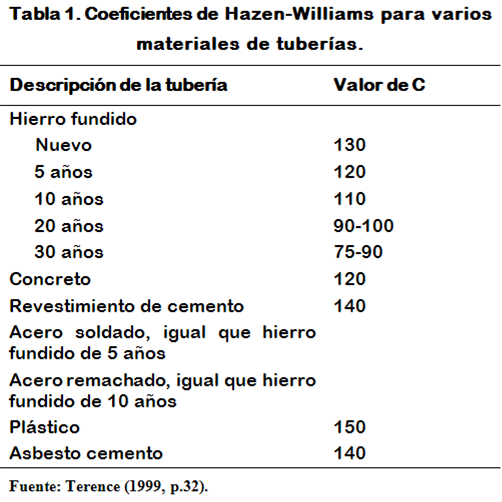

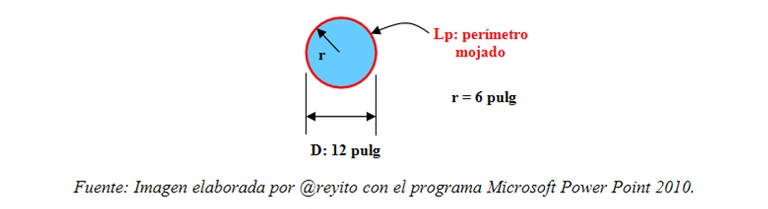
Es el área del tubo dividida por el perímetro mojado. ¿Cómo se interpreta físicamente? Para entender su significado es preciso que imaginemos una tubería de sección transversal “A” que trasiega agua a sección llena. Entonces el área ocupada por el flujo es “A”, por lo tanto el fluido moja todo el perímetro interno de la sección transversal, en este caso de la circunferencia. Veámoslo gráficamente en la Figura 1.
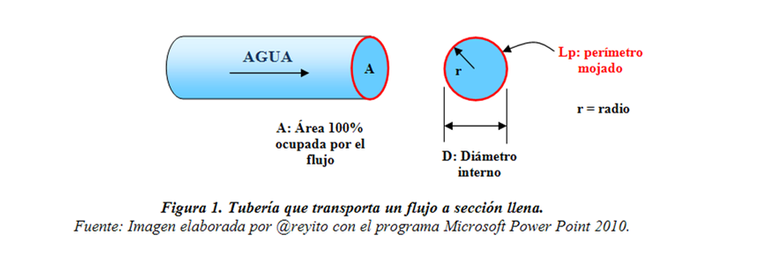
El área ocupada por el flujo es:
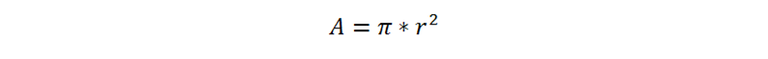
El perímetro mojado, identificado en la Figura 1 con el color rojo, corresponde al perímetro de la circunferencia y viene dado por:
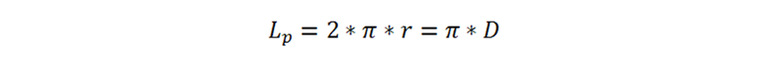
Aplicamos la definición de radio hidráulico: Es el área del tubo dividida por el perímetro mojado. Entonces:
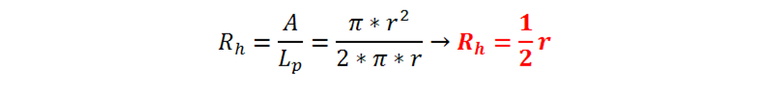
Pero r = D/2, por lo tanto:
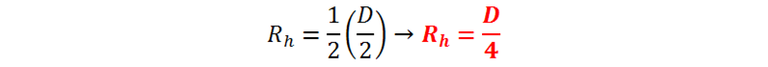
Aunque parece un concepto elemental, en realidad no es así. ¿Por qué? Porque al analizar un problema de conducción de agua en una tubería debemos tener presente si el fluido ocupa la sección completa de la misma, o si por el contrario ocupa una fracción de ésta lo cual afectaría el valor del radio hidráulico. Los problemas donde se aplica la FHW consideran la sección 100% llena de agua.

Algo tan simple como esto:
Perímetro mojado:
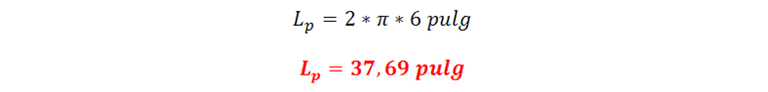
Radio hidráulico:
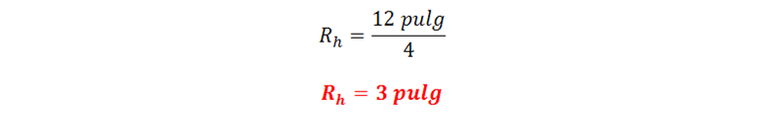

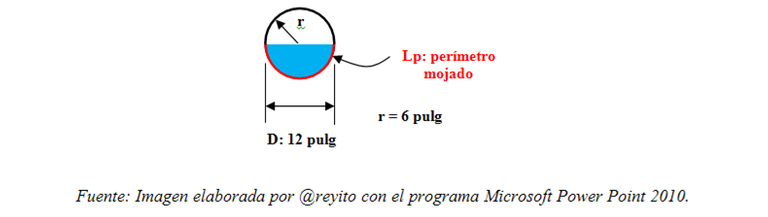
- Perímetro mojado: Debido a que el área ocupada por el flujo es la mitad de la sección del tubo, entonces el perímetro mojado es la mitad del perímetro de la circunferencia.
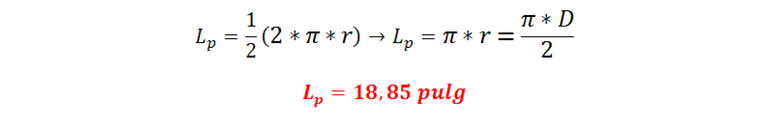
- Radio hidráulico: Aplicando la definición, resulta lo siguiente.
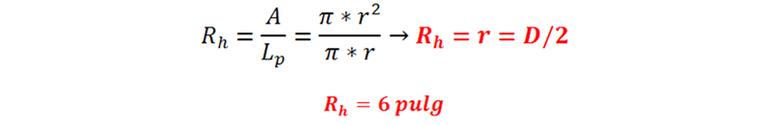
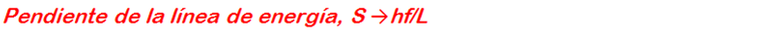
La Ec. 1 y sus equivalentes (Ec. 2 y Ec. 3) no muestran de una manera explícita cómo determinar las pérdidas por longitud en una tubería. No obstante, nos valdremos de algunos artificios matemáticos básicos con el objeto de transformar la Ec. 1 de manera tal que podamos utilizarla con el propósito no de determinar la velocidad del flujo, sino de cuantificar las pérdidas primarias.
Procedimiento para transformar la FHW:
- Sustituir en la Ec. 2 el factor “S” por la pendiente de la línea de energía
.
- De igual manera, la velocidad “v” (m/s) que adquiere el flujo “Q” (
) trasegado en una tubería cuya sección transversal es “A” (
), viene dada por:
.
Luego:
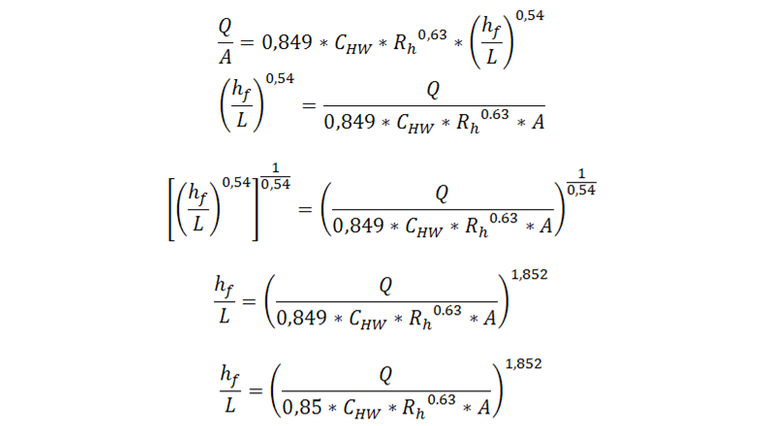
Reemplazamos el radio hidráulico 

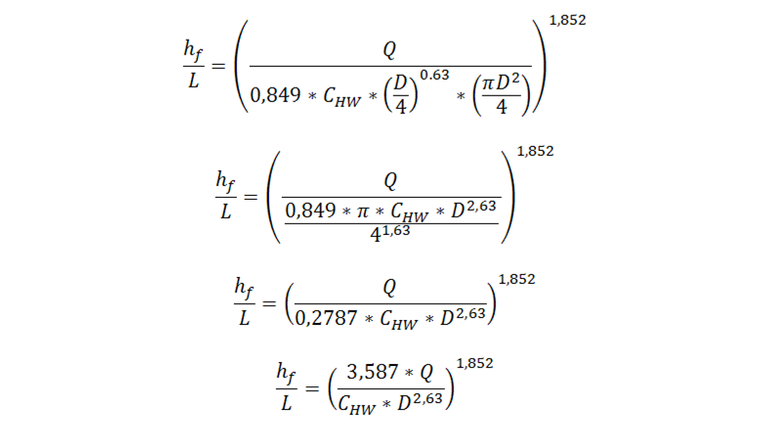
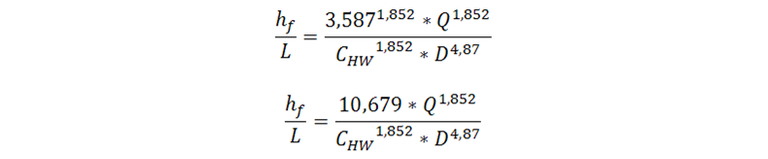
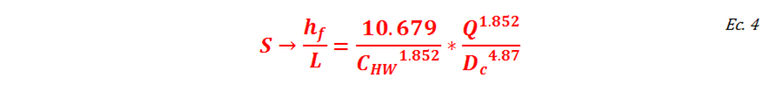
La expresión anterior indica la cantidad de presión que se pierde en un tramo de tubería por cada unidad de longitud.
Observación:
Es importante no perder de vista que la constante k = 10,679 tiene que ver con el hecho de suponer que la tubería conduce agua a sección llena, en cuyo caso el radio hidráulico equivale a la cuarta parte del diámetro interno del tubo, tal como se demostró previamente. Por lo tanto, si la tubería no está cargada totalmente, el radio hidráulico tendría un valor distinto al indicado y en consecuencia la fórmula tal como está escrita no aplicaría porque cambiaría el valor de la constante "k".

Simplemente se obtienen al multiplicar la pendiente de la línea de energía por la longitud de la tubería que trasiega un determinado flujo de agua. En consecuencia, la FHW quedaría de la siguiente manera:



Esta fórmula en sus inicios se consideraba como una simple herramienta para la elaboración de cálculos de pérdidas de energía en tuberías que transportan agua, la ecuación considera el coeficiente de rugosidad CHW asumido como constante para cierto material de la tubería, a pesar del tamaño del tubo o el rango de flujo. Mott (2006), afirma lo siguiente: “su uso se limita al flujo de agua en tuberías con diámetros mayores de 2.0 pulg y menores de 72 pulg (6.0 pies). La velocidad del flujo no debe exceder los 10.0 pies/s (3 m/s). Asimismo, está elaborada para agua a 60 °F” (p.244). Por tal motivo el empleo en condiciones que no estén en el rango anterior ocasionaría cierto error al momento de su aplicación. La FHW se vale de las características de la tubería, pero no toma en cuenta las propiedades del fluido tales como la densidad, peso específico, viscosidad dinámica ni la viscosidad cinemática. Por lo tanto, debe quedar claro que esta es tal vez la razón principal por la cual no aplica en análisis de fluidos distintos al agua.

Observación: Se tomó para la tubería de acero el valor de C = 120 indicado en la Tabla 1 para “Acero soldado, igual que hierro fundido de 5 años.”


Podemos convertir este resultado en “psi” (libras por pulgadas cuadradas) que es una unidad de presión comúnmente utilizada. Factor de conversión: 1 psi → 0,704 m.c.a. Por lo tanto:
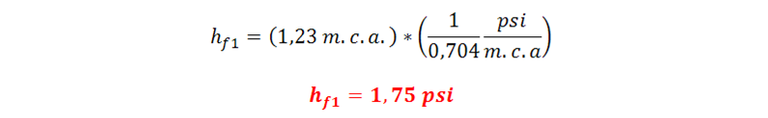
Razonamiento: Desde el punto “A” hasta el punto “B” se produce una pérdida o caída de presión equivalente a 1,23 m.c.a. (1,75 psi) en la tubería de 54 pulgadas, al trasegar un caudal de 1.500 l/s.
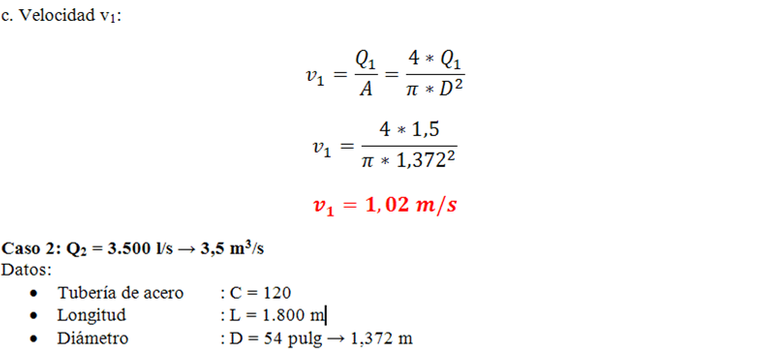

Podemos convertir este resultado en “psi” (libras por pulgadas cuadradas) que es una unidad de presión comúnmente utilizada. Factor de conversión: 1 psi → 0,704 m.c.a. Por lo tanto:
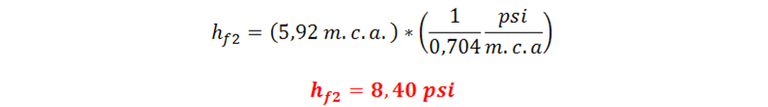
Razonamiento: Desde el punto “A” hasta el punto “B” se produce una pérdida o caída de presión equivalente a 5,92 m.c.a. (8,40 psi) en la tubería de 54 pulgadas, al trasegar un caudal de 3.500 l/s.
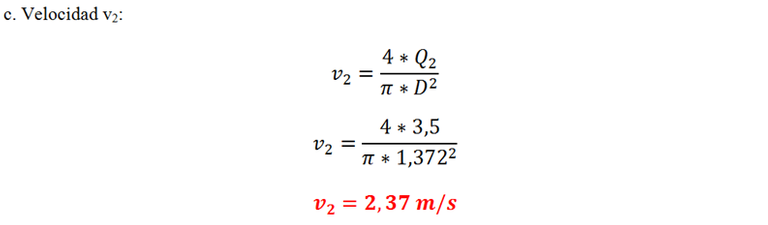
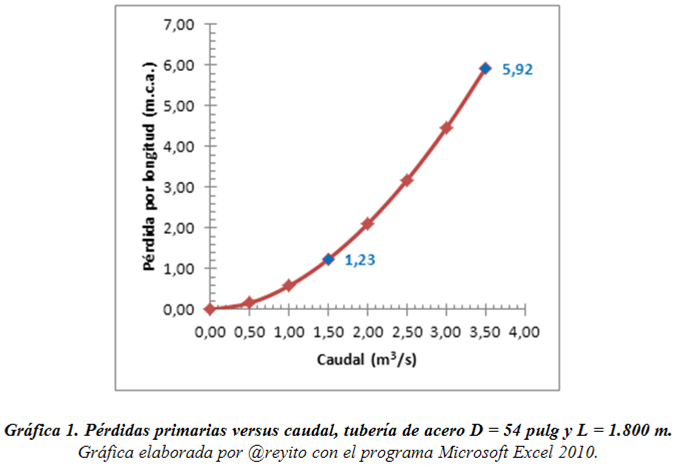
La Gráfica 1 permite observar la forma cómo varían las pérdidas primarias con el caudal en el ejercicio 3.
Observaciones relativas al ejercicio 3:
- Las pérdidas de presión se incrementaron de 1,23 m.c.a. (1,75 psi) hasta 5,92 m.c.a. (8,40 psi) al aumentar el flujo en la tubería de 54 pulgadas, de 1.500 l/s a 3.500 l/s.
- Como era de esperarse, la velocidad del flujo aumentó de 1,02 m/s a 2,37 m/s. ¿Por qué? Porque se ha incrementado el caudal manteniendo el mismo el diámetro.
- ¿Que deberíamos hacer si la velocidad obtenida excediese el límite establecido por alguna normativa legal vigente? La respuesta sería esta: Deberíamos aumentar el diámetro de la tubería para poder bajar la velocidad del flujo, si la idea es suministrar un determinado caudal. Lo anterior implicaría aumento en los costos totales de la obra. Por ejemplo, si se tratase del diseño de una estación de bombeo, lo más recomendable sería efectuar un análisis técnico económico que conduzca a minimizar el efecto global de los gastos de energía más los gastos de inversión dando como resultado final la obtención del diámetro económico. Esta idea se sugiere en la Gráfica 2.
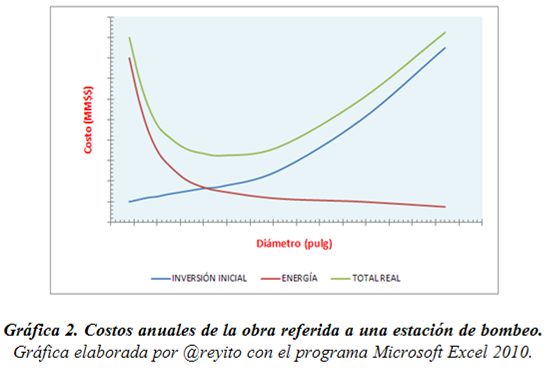
El aspecto más importante que muestra la Gráfica 1, es que existe un diámetro de tubería para el cual el costo total anual se ubica en el punto mínimo de la curva resultante, y no es otro que el diámetro económico. Podemos ver que si escogemos un diámetro muy pequeño la inversión inicial es baja pero los costos de energía anuales se disparan. ¿Por qué? Porque estaríamos obligados a colocar bombas con motores eléctricos cuyas potencias serían relativamente elevadas dado que las pérdidas primarias (explicadas en este documento) se incrementarían considerablemente, vale decir, que las velocidades en esta condición serían también relativamente elevadas pudiendo inclusive exceder los límites que señalan las normas vigentes. El escenario se invierte si escogemos un diámetro muy grande, en cuyo los gastos anuales de energía bajan considerablemente requiriendo la colocación de bombas y motores de menor capacidad mientras y por otro lado se elevarían exageradamente los gastos que atañen a la inversión inicial, pero habría que analizar la relación “costos/beneficios” y toda posibilidad de retorno de capital que la inversión pudiese acarrear, lo cual a la larga no da buenos resultados. En síntesis, lo correcto es realizar el estudio técnico-económico de la obra a diseñar a los fines de obtener con criterios de ingeniería el diámetro económico y por lo tanto minimizar los costos totales anuales.

Una vez presentado este documento, se concluye lo siguiente:
- La fórmula de Hazen-Williams (FHW) permite cuantificar las pérdidas primarias en una tubería que trasiega agua a sección llena. El cálculo no toma en cuenta las propiedades físicas del agua (densidad, peso específico, viscosidad absoluta y relativa), y solo se basa en un coeficiente de rugosidad (CHW) vinculado al material con que están fabricadas las tuberías, y del radio hidráulico que a su vez depende de la sección transversal de la conducción y del perímetro mojado.
- La FHW tiene un uso muy limitado por cuanto no aplica para fluidos diferentes al agua.
- Vale señalar que en Europa se utiliza más la fórmula de Darcy-Weisbach, la cual explicaré en otro documento; esta última aplica para cualquier tipo fluido incluyendo el agua y toma en cuenta las propiedades físicas de éstos. No obstante, expertos en hidráulica consideran que para fines prácticos en lo que respecta al diseño de redes de abastecimiento, la FHW arroja resultados confiables; de hecho, en EE.UU es comúnmente utilizada con este propósito y su uso se ha extendido a nivel internacional.
- Su uso, según Mott (2006), se limita al flujo de agua en tuberías con diámetros mayores de 2.0 pulg y menores de 72 pulg (6.0 pies). El referido Autor afirma que la velocidad del flujo no debe exceder los 10.0 pies/s (3 m/s). Asimismo, está elaborada para agua a 60 °F” (p.244).
- La pendiente de la línea de energía la podemos calcular mediante la Ec. 4 y las pérdidas primarias la obtenemos con la Ec. 5.



Excelente trabajo @reyito, esperando por la explicación de la formula de Darcy-Weisbach.
Hola, @luiscd8a, gracias por mostrar interés en leer esta publicación, espero que te haya servido de algo. Pronto, Dios mediante, publicaré sobre la ecuación de Darcy-Weisbach. Te saluda un amigo en la distancia.
Impresionante lo felicitamos..
Hola, @votovzla, muchas gracias por considerar como impresionante el artículo que he publicado. Espero le sea de mucha utilidad a usted y a sus amigos. Saludos cordiales.