INTRODUCCIÓN
A continuación nos adentraremos en el estudio de una propiedad presente en los sistemas estructurales, que no se distingue a simple vista, como sucede con los componentes de masa (m) y rigidez (k), pero si estamos convencidos de su presencia, porque es la responsable de que la vibración libre que experimenta una estructura decaiga con el tiempo; esta propiedad recibe el nombre de amortiguamiento, se suele idealizar con el elemento en color verde de la imagen N°01, y busca representar aquellos mecanismos de disipación de energía dentro del rango elástico lineal, como lo pueden ser la fricción y el calor que se genera en lo más íntimo de los componentes estructurales.
Imagen N°01: enfoque global de los temas a estudiar
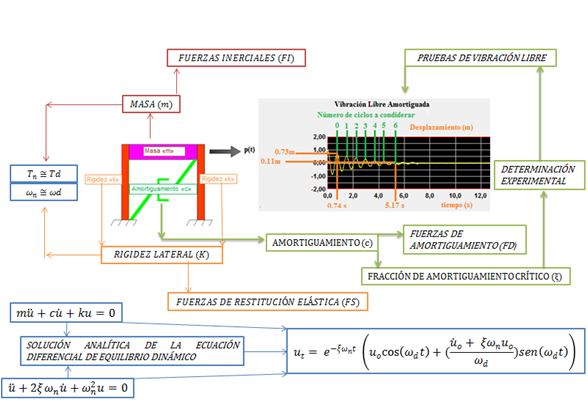
Fuente: Chopra (2014), NONLIN V 7.14, adaptada por Santana (2018)
Esta propiedad de amortiguamiento contextualizada al caso de estructuras de interés en el campo de la ingeniería sismoresistente, al introducirse en la ecuación de equilibrio dinámico del sistema estructural, representada por una ecuación diferencial lineal de segundo orden, crea un reto en la solución analítica de la misma, siendo necesario recurrir a la técnica de Euler y el determinante de Wronskiano para dar con dicha solución. Por tal razón, realizaremos un abordaje matemático del concepto de amortiguamiento, lo cual sustenta el método que utilizaremos para estimar la fracción de amortiguamiento crítico (ξ), a partir de ensayos de vibración libre; este método se conoce como “decremento logarítmico”. Al mismo tiempo este enfoque matemático del concepto de amortiguamiento, permite sustentar la demostración analítica y práctica, de como las propiedades dinámicas en condición natural (período natural “Tn”, frecuencia natural “ɷn”), son aproximadamente iguales, a las propiedades dinámicas en condición amortiguada (período amortiguado “Td”, frecuencia amortiguada “ɷd”). Realicemos a continuación una delimitación de la temática a estudiar.
DELIMITACIÓN DE LA TEMÁTICA EN ESTUDIO
Se recomienda al lector, revisar la referencia N°04, a los fines de profundizar en el proceso de obtención de la rigidez lateral, masa, y propiedades dinámicas naturales de un pórtico plano de un grado de libertad. En la imagen N°02 se aprecia un pórtico con tres componentes fundamentales, referidos a la masa (m), amortiguamiento (c) y rigidez (k). Se le aplica una fuerza externa p(t), que lo perturba del estado de reposo, para posteriormente dejarlo vibrar libremente.
Imagen N°02: pórtico plano sometido en régimen de vibración libre
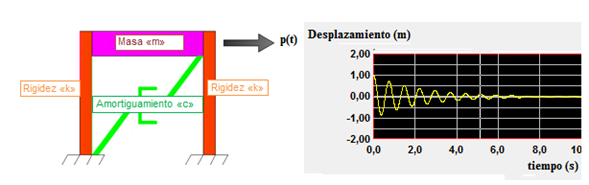
Fuente: NONLIN V 7.14, adaptada por Santana (2018)
Con la ayuda del principio de D’Alembert, podemos desarrollar el diagrama de cuerpo libre del problema en estudio (ver imagen N°03), donde aparecen fuerzas inerciales (fi), elásticas (fs) y de amortiguamiento (fd), que se oponen a la vibración impuesta; dichas fuerzas se asocian a las propiedades estructurales de masa, rigidez y amortiguamiento respectivamente. Esto permite plantear la ecuación de equilibrio dinámico del sistema:
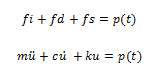
Imagen N°03: diagrama de cuerpo libre
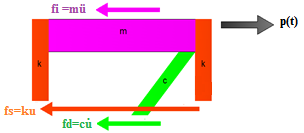
Fuente: Santana (2018)
Adicionalmente, dado que el rol de la fuerza externa p(t), es el de iniciar la vibración del sistema estructural, para luego ser retirada (dejando al sistema en vibración libre), se puede considerar su valor como cero “0”, lo que permite reescribir la ecuación de equilibrio dinámico de la siguiente manera:
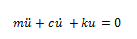
Al dividir la ecuación de equilibrio dinámico por la masa “m”, se obtiene:
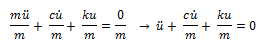
Las constantes naturales de la estructura referidas a la masa (m) y rigidez (k), pueden ser presentadas en términos de la frecuencia natural (ωn):
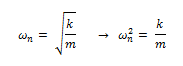
Por lo tanto:
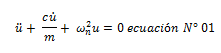
Al mismo tiempo, vale introducir un concepto de mucho interés práctico en la dinámica estructural, como lo es la fracción de amortiguamiento crítico “ξ”; por lo que la ecuación N°01 se puede reescribir así:
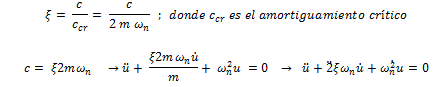
Una forma didáctica de comprender el significado de amortiguamiento crítico “ccr”, es la siguiente:
Imagen N°04: interpretación didáctica del amortiguamiento crítico
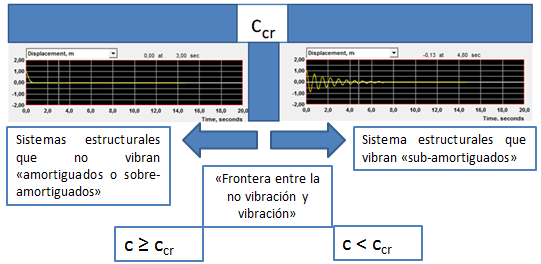
Fuente: NONLIN V 7.14, adaptado por Santana (2018)
El mapa conceptual de la imagen N°04 nos deja claro, que cuando la constante de amortiguamiento “c”, es mayor o igual al amortiguamiento crítico, el sistema simplemente no vibra, mientras que cuando ocurre lo contrario, si existe vibración, la cual decaerá en el tiempo, en función del cociente que resulta de dividir el amortiguamiento “c” con el amortiguamiento crítico “ccr”, conocido como la fracción de amortiguamiento crítico “ξ”. En base a esto, Chopra (2014) señala que todas las estructuras de interés en el campo de la ingeniería sismoresistente, como lo son edificios, puentes, presas, centrales nucleares y otras, presentan una fracción de amortiguamiento crítico “ξ <0.10”. De allí a que la ecuación diferencial que rige el equilibrio dinámico del sistema estructural, se resolverá dando preferencia a esta condición.
Una vez resuelta dicha ecuación diferencial, tendremos el sustento matemático, en el cual se fundamenta el “método de decremento logarítmico”, que se aplica a registros de ensayos de vibración libre realizado a estructuras, para estimar la fracción de amortiguamiento crítico “ξ” de estas, y por ende, de manera indirecta la constante de amortiguamiento “c”.
RESOLVIENDO LA ECUACIÓN DIFERENCIAL DE EQUILIBRIO DINÁMICO
La ecuación de equilibrio dinámico del sistema estructural en estudio, de la forma:
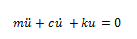
Es una ecuación diferencial lineal de segundo orden, cuya solución en términos de desplazamiento (ut) se rige con la siguiente expresión:
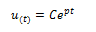
Al obtener la primera y segunda derivada con respecto al tiempo de la solución planteada, la misma puede expresarse en términos de velocidad (ůt) y aceleración (üt), respectivamente:
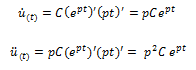
Si sustituimos las soluciones planteadas en la ecuación de equilibrio dinámico del sistema, obtenemos lo siguiente:
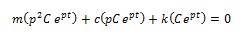
Sacamos factor común:
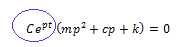
Hemos llegado a una ecuación homogénea con coeficientes constantes, la cual tiene la particularidad de que el término resaltado en color azul nunca se anula, por lo que la ecuación se cumple si y sólo si:
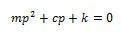
Por lo tanto debemos encontrar el valor de “p”; de allí que al aplicar la técnica de la resolvente para un polinomio de orden dos, obtenemos:
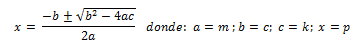
Sustituyendo:
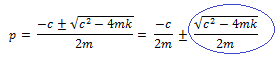
El término resaltado en color azul, vamos a representarlo con la letra “g”, y lo reescribiremos en función de la frecuencia natural y de la fracción de amortiguamiento crítico (ξ). En primera instancia nos valemos del siguiente artificio:
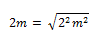
De tal manera que:
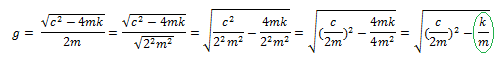
Si despejamos de la expresión de fracción de amortiguamiento critico el término “2m”, de la forma:
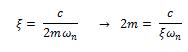
Y expresamos el término resaltado en color verde, en función de la frecuencia natural:
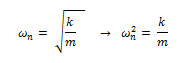
Obtenemos que:
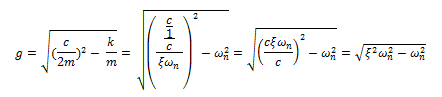
Sacamos factor común “ɷn”:
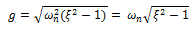
De esta manera las soluciones para la ecuación:
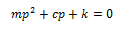
Están representadas por:
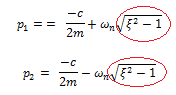
De acuerdo a lo que se explicó en el tópico concerniente a “DELIMITACIÓN DE LA TEMÁTICA EN ESTUDIO”, las estructuras de interés en el campo de la ingeniería sismoresistente son aquellas que presentan una fracción de amortiguamiento crítico “ξ<0.10”; de manera que al sustituir este valor en el término resaltado en color rojo que para fines prácticos denominaremos “z”, da como resultado:
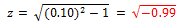
Por lo que tendríamos una raíz negativa que tendría una solución compleja, de la forma:
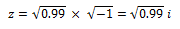
Basados en este sencillo ejemplo numérico, el término “z” puede ser reescrito de forma general:
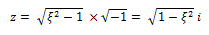
Por lo tanto, las soluciones p1 y p2, pueden expresarse de la siguiente manera:
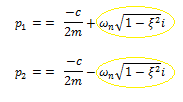
El término resaltado en color amarillo es la frecuencia amortiguada del sistema “ɷd”;por lo que las soluciones se reescriben de la forma:
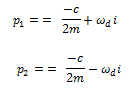
Surge la cuestión, de que la solución de la ecuación de equilibrio dinámico en términos de desplazamiento de la forma:
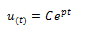
Estará constituida por términos complejos, y como son dos valores de “p” tendríamos dos soluciones complejas, lo que sugiere la aplicación de la técnica de Euler para encontrar así las soluciones reales que nos interesan. En la imagen N°05 se ilustra didácticamente el proceso de aplicación de Euler, omitiendo voluntariamente la constante “C”, para posteriormente ser introducida en la solución general, en forma de constantes de integración “A” y “B”.
Imagen N°05: aplicación de Euler, para encontrar las soluciones reales de la ecuación diferencial en estudio
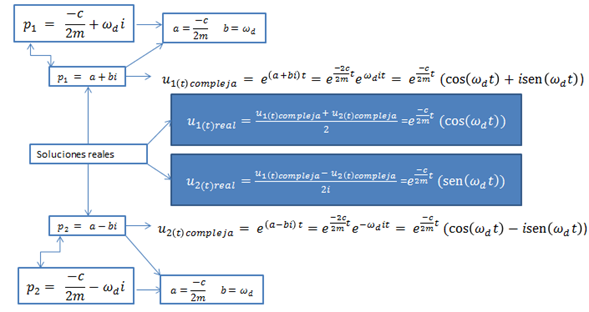
Fuente: Santana (2018)
En el establecimiento de la solución general de la ecuación diferencial que representa el equilibrio dinámico de un sistema en régimen de vibración libre amortiguada, es necesario demostrar que las soluciones reales obtenidas sean linealmente independientes, por lo que se aplica el determinante Wronskiano; siendo necesario obtener la primera derivada con respecto al tiempo de las soluciones reales. En el caso de la solución real N°01:
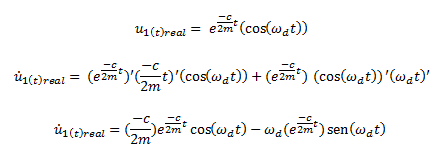
Con respecto a la solución real N°02:
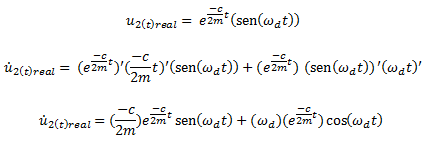
La aplicación del determinante de Wronskiano, la podemos apreciar ilustrada de forma didáctica en la imagen N°06:
Imagen N°06: desarrollo del “Determinante de Wronskiano”
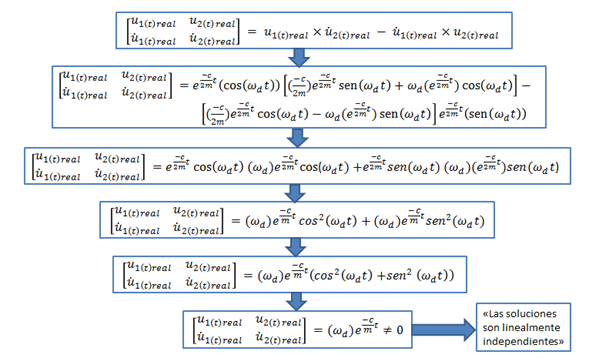
Fuente: Santana (2018)
De acuerdo al resultado obtenido de la aplicación del determinante de Wronskiano, las soluciones reales en términos de desplazamiento son linealmente independientes, lo que significa que se puede expresar la solución general, como la suma de ambas:
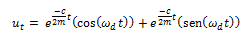
Introducimos las constantes de integración “A” y “B”:
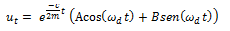
De la expresión de fracción de amortiguamiento crítico, se tiene lo siguiente:
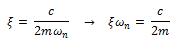
Por lo que la solución general puede ser expresada así:
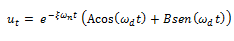
Para encontrar las constantes de integración “A”, y “B”, obtenemos la primera derivada con respecto al tiempo de la solución general:
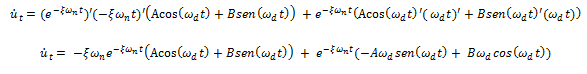
La solución general en términos de desplazamiento evaluada en el instante de tiempo t=0, da como resultado:
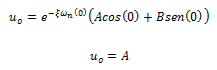
Por su parte al evaluar la solución general en términos de velocidad para el instante de tiempo t=0, permite obtener:
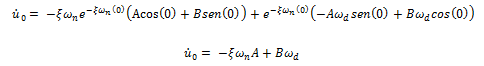
Dado que A = uo, entonces:
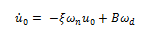
Despejamos la constante de integración B:
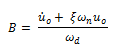
Por lo que la solución general que describe el desplazamiento en el tiempo, de un sistema en vibración libre con amortiguamiento es:
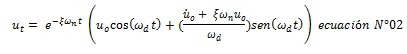
DEMOSTRACIÓN ANALÍTICA Y GRÁFICA DEL EFECTO DEL AMORTIGUAMIENTO EN LAS PROPIEDADES DINÁMICAS DE PERÍODO Y FRECUENCIA
En la referencia N°04, se hace un estudio sobre las propiedades dinámicas naturales de la estructura en un régimen de vibración libre sin amortiguamiento (periodo natural “Tn” y frecuencia natural “ɷn”), y se define la solución general que determina la respuesta en términos de desplazamiento en el tiempo. La cual también se puede obtener a partir de la ecuación N°02, estableciendo la fracción de amortiguamiento crítico “ξ =0” y la frecuencia amortiguada “ɷd” expresarla en términos de frecuencia natural “ɷn”, las cuales como se demostrará en las próximas líneas, son aproximadamente iguales, por lo que se permite hacer esta operación:
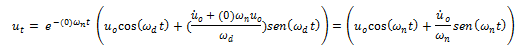
En esta oportunidad compararemos esta respuesta con la de un sistema que presenta amortiguamiento, regido por la ecuación N°02. En la gráfica de la imagen N°07 podemos visualizar esta comparación.
Imagen N°07: influencia del amortiguamiento en la vibración libre
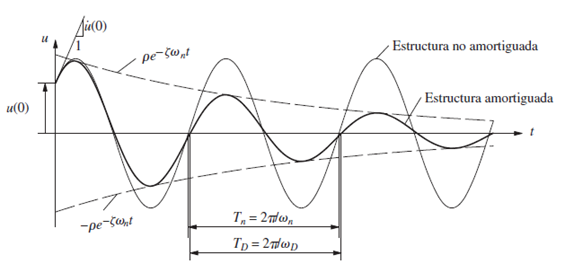
Fuente: Chopra (2014)
Nos damos cuenta, como el efecto del amortiguamiento hace que la amplitud decaiga con el tiempo, a diferencia de lo que ocurre en una estructura no amortiguada, cuya amplitud se mantiene constante a lo largo del tiempo. Podemos apreciar también que el periodo natural (Tn), es aproximadamente igual al período amortiguado (Td). Lo cual tiene el siguiente sustento analítico, ilustrado didácticamente en la imagen N°08:
Imagen N°08: demostración analítica del efecto del amortiguamiento en las propiedades dinámicas
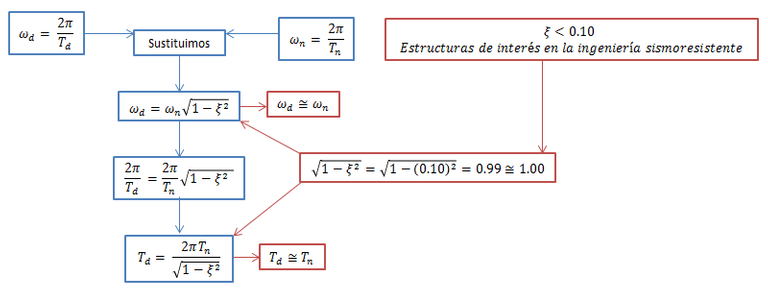
Fuente: Santana (2018)
En base a lo expuesto en la imagen N°08, podemos concluir que las propiedades dinámicas naturales con o sin amortiguamiento, son aproximadamente iguales, es por ello, que al momento de expresarnos al periodo o frecuencia de la estructura, sea esta amortiguada o no, no se hace mayor distinción.
OBTENCIÓN EXPERIMENTAL DE LA FRACCIÓN DE AMORTIGUAMIENTO CRÍTICO, CON LA TÉCNICA DEL DECREMENTO LOGARÍTMICO
La obtención experimental del amortiguamiento en una estructura, a través de pruebas de vibración libre, tiene su sustento en el decaimiento de la amplitud en el tiempo que esta experimenta, como se aprecia en la gráfica de la imagen N°07; se puede decir, que entre dos picos sucesivos, separados por un tiempo igual al periodo amortiguado “Td”, la razón del decaimiento de la amplitud es:
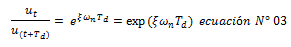
Si establecemos:
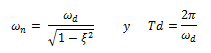
Y sustituimos en la ecuación N°03:
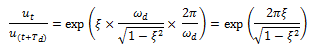
El logaritmo natural de esta expresión, es el decremento logarítmico, por lo tanto al aplicar logaritmo natural, la exponencial se cancela, quedando lo siguiente:
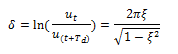
Como se demostró en la imagen N°08, el término:
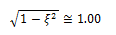
Por lo que el decremento logarítmico, se puede expresar así:
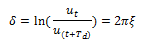
Si despejamos fracción de amortiguamiento crítico:
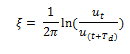
De forma general esta expresión se reescribe de la siguiente manera:
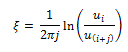
Y aplica también para el caso que se tengan registros de aceleraciones, es decir:
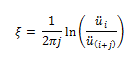
Vale destacar que “j” indica la cantidad de ciclos contados a partir del punto de referencia “i”. En el siguiente tópico se realiza un ejemplo práctico, donde queda más claro la aplicación de esta fórmula de decremento logarítmico, trascendental para la determinación experimental del amortiguamiento en estructuras, a través de pruebas de vibración libre.
DESARROLLO DE EJEMPLO PRÁCTICO
En la imagen N°09, se representan los datos del problema que esteremos tomando como referencia para estimar la fracción de amortiguamiento crítico (ξ); consistente en un pórtico plano, de un grado de libertad, al que se le conocen sus propiedades de masa y rigidez. Se recomienda al lector, revisar la referencia N°04, donde se profundiza en el cálculo de estas propiedades.
Imagen N°09: ilustración de los datos del problema en estudio
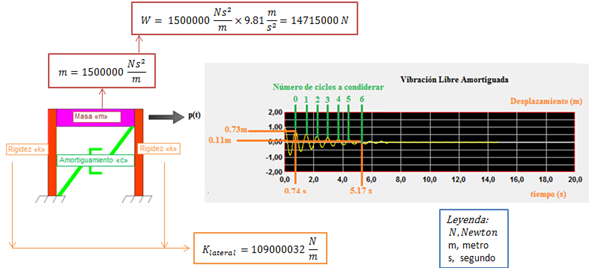
Fuente: NONLIN V 7.14 adaptado por Santana (2018)
Los datos de entrada en la fórmula de decremento logarítmico son:
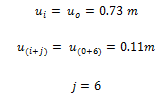
Aplicamos la fórmula en cuestión:
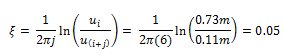
Adicionalmente podemos calcular de forma experimental las propiedades dinámicas, de la siguiente manera:
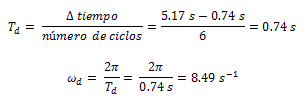
Dado que las propiedades de masa (m) y rigidez (k) son conocidas, aprovecharemos de calcular frecuencia natural y periodo natural, para contrastarlo con el periodo y frecuencia amortiguada, y así demostrar con este ejemplo práctico como estos valores tienden a ser iguales.
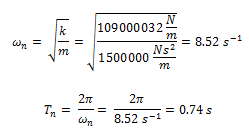
Finalmente a partir de la expresión de fracción de amortiguamiento crítico, podemos encontrar la constante de amortiguamiento “c” de forma indirecta:
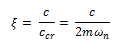
Despejamos “c”, y sustituimos los datos conocidos:
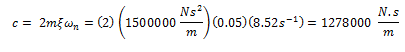
En la tabla N°01, se presenta un resumen de resultados:
Tabla N°01: resumen de resultados obtenidos

Fuente: Santana (2018)
Las casillas resaltadas de la tabla N°01, representan las propiedades obtenidas de forma experimental.
CONCLUSIONES
1.- La propiedades dinámicas en condición natural y amortiguada, tienden a ser iguales, para la fracción de amortiguamiento crítico "ξ<0.10".
2.- La fracción de amortiguamiento crítico "ξ<0.10", es un valor de referencia utilizado para modelar las estructuras de interés en el campo de la ingeniería sismoresistente, como puentes, edificios y otras.
3.- El amortiguamiento en estructuras que se encuentran en rango elástico, se asocia al calor y la fricción que se produce en los elementos estructurales sometidos a vibración.
4.- Los mecanismos de disipación de energía asociados a un comportamiento inelástico de la estructura, como por ejemplo, presencia de daño controlado en los elementos estructurales, requiere del uso de modelos histeréticos de disipación de energía; no obstante, lo abordado en este artículo, es base, para adentrarnos a estos temas de mayor complejidad en el campo de la ingeniería sismoresistente.
REFERENCIAS CONSULTADAS
1.- CHOPRA ANIL K.DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACION, MEXICO 2014.
2.- SIMMONS GEORGE Y ROBERTSON JOHN. ECUACIONES DIFERENCIALES CON APLICACIONES Y NOTAS HISTÓRICAS, MCGRAW-HILL, MADRID 1998.
3.-.NONLIN “EDUCATIONAL PROGRAM FOR LEARNING THE CONCEPTS OF STRUCTURAL DYNAMICS AND EARTHQUAKE ENGINEERING”. DEVELOPED BY DR. FINLEY CHARNEY, NONLIN is available as online tool through NEEShub: http://nees.org/
4.- SANTANA ELÍAS. COMPRENDIENDO LAS APLICACIONES DE LAS MATEMÁTICAS EN LA ESTIMACIÓN DEL PERIODO Y FRECUENCIA NATURAL DE UN PORTICO PLANO. CASO: SISTEMA DE UN GRADO DE LIBERTAD. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/comprendiendo-las-aplicaciones-de-las-matematicas-en-la-estimacion-del-periodo-y-frecuencia-natural-de-un-portico-plano-caso
A veces es bueno enumerar las ecuaciones para poder realizar un mejor seguimiento y no perderse en la lectura, en mi caso lo entiendo perfectamente, pero recuerda que en la comunidad hay diferentes tipos de lectores que no son especialistas en ecuaciones diferenciales o matemática simple y entonces es difícil para ellos. De todas maneras excelente post elias
Gracias @carloserp-2000, es una acotación que tendré en cuenta, en el desarrollo de futuros artículos contentivos de deducciones matemáticas. Me complace leer tu comentario. Saludos!
Siendo un SteemStem Estados
Excelente post Elias! muy pero muy bien explicado, aunque no soy ingeniero me encanta la matemática, y trato de conectar con stemians que comparta contenido como este, me gustaría invitarte a que pases por mi blog pero para que te unas a mi comunidad, sé que a mis amigos también les gustarían mucho tus publicaciones, y viendo que tienes experiencia me gustaría invitarte a ser uno de los administradores.
Gracias @erikatrend, complacido por la invitación que haces, me puedes contactar vía:
Discord: eliaschess333#3712
Saludos!
te voy a escribir! te puedes pasar por mi ultimo post para que toques el enlace de la comunidad y conozcas al resto de mis amigos también, te espero!
Excelente post, soy nueva de esta gran comunidad espero contar con tu apoyo...
Gracias @bigdesafios, bienvenida. Saludos!