[ESP]
¡Hola hermosa comunidad de Hive! 👋
Hoy nos seguiremos sumergiendonos en el fascinante mundo de las derivadas. 🧠🔍 Este conocimiento es crucial para comprender y resolver problemas complejos, incluyendo la resolución de circuitos eléctricos en futuras lecciones. 🚀⚡
Continuando con nuestro recorrido por el fascinante mundo de las derivadas
Quiero compartir con ustedes 10 ejemplos prácticos resueltos. Estos ejercicios no solo reforzarán tus conocimientos, sino que también te mostrarán cómo aplicar las derivadas en problemas de electrónica. 📐⚡ Las derivadas son una herramienta poderosa en el análisis y diseño de circuitos, especialmente cuando tratamos con señales variables en el tiempo. ¡Vamos a sumergirnos en estos ejemplos!
Ejemplo 1: Derivada de una Función Lineal
- Función:
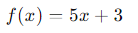
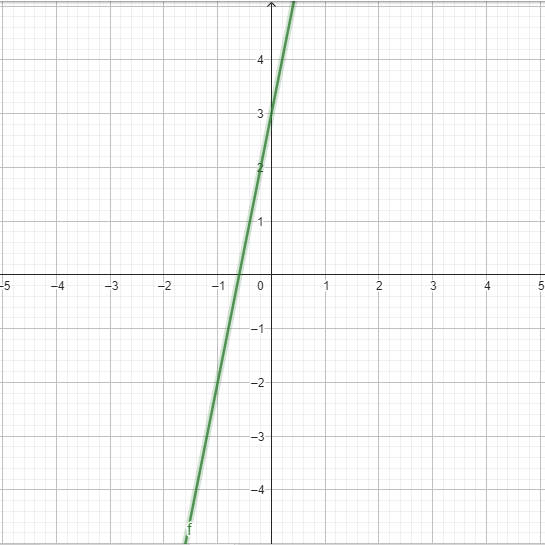
Paso a Paso:
- 1. Identificamos los términos de la función: 5𝑥 y 3.
- 2. La derivada de una constante (3) es 0.
- 3. La derivada de 5𝑥 es 5 (coeficiente de 𝑥).
- 4. Sumamos las derivadas.
Derivada:
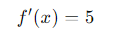
Explicación:
La derivada de una función lineal es simplemente la pendiente de la línea. En este caso, la pendiente es 5, lo que significa que por cada unidad que aumentamos en 𝑥, 𝑓(𝑥) aumenta en 5 unidades.
Ejemplo 2: Derivada de una Función Cuadrática
- Función:
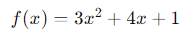
Paso a Paso:
- 1. Derivamos 3𝑥2 : bajamos el exponente y multiplicamos por el coeficiente: 2⋅3𝑥2−1 = 6𝑥.
- 2. Derivamos 4𝑥: el coeficiente es la derivada (4).
- 3. La derivada de una constante (1) es 0.
- 4. Sumamos las derivadas.
Derivada:
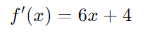
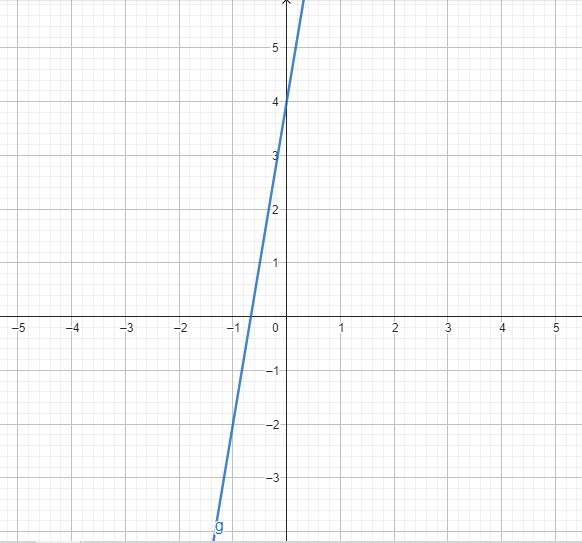
Explicación:
La derivada de una función cuadrática es una función lineal. Esto nos da la pendiente de la tangente a la curva en cualquier punto 𝑥, indicando cómo cambia la función a medida que movemos 𝑥.
Ejemplo 3: Derivada de una Función Cúbica
- Función:
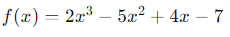
Paso a Paso:
1. Derivamos:
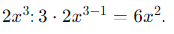
2. Derivamos:
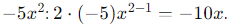
3. Derivamos 4𝑥: el coeficiente es la derivada (4).
4. La derivada de una constante (-7) es 0.
5. Sumamos las derivadas.
Derivada:
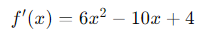
Explicación:
La derivada de una función cúbica es una función cuadrática, lo que nos muestra cómo la tasa de cambio de la función no es constante, sino que varía de manera no lineal a medida que movemos 𝑥.
Ejemplo 4: Derivada de una Función Trigonométrica (Seno)
- Función:
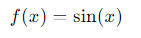
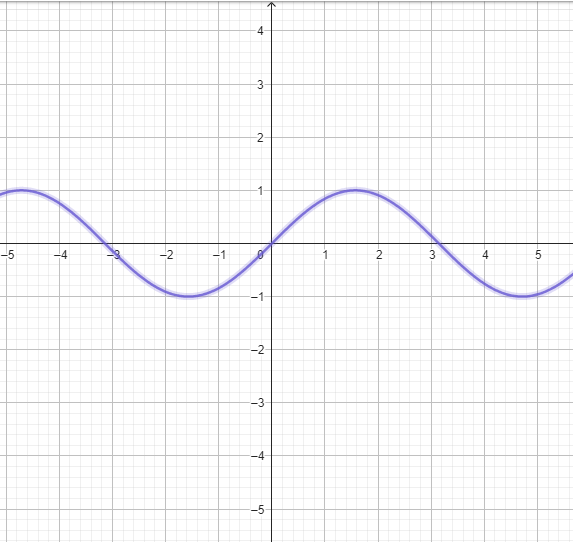
Paso a Paso:
La derivada de sen(𝑥)es cos(𝑥).
- Derivada:
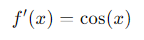
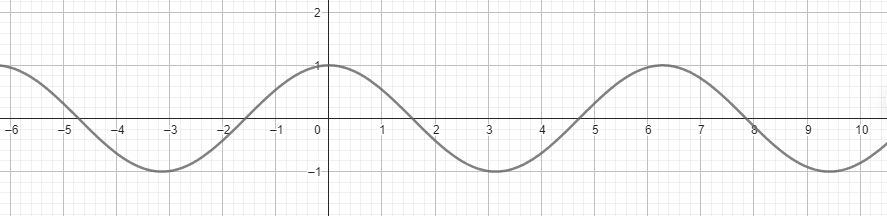
Explicación:
En electrónica, las funciones seno y coseno son fundamentales para describir señales de corriente alterna (CA). Saber cómo derivar estas funciones es crucial para entender cómo varían estas señales con el tiempo. para conocer mas sobre esto te ivito a que veas mi post dedicado a la corriente alterna
Ejemplo 5: Derivada de una Función Trigonométrica (Coseno)
- Función:
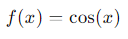
Paso a Paso:
- 1. La derivada de cos (𝑥) es −sen(𝑥).
Derivada: 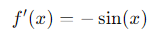
Explicación:
La derivada del coseno es el negativo del seno, lo que refleja cómo la pendiente de la función coseno cambia en cada punto. Esto es útil cuando analizamos la fase de las señales en un circuito.
Ejemplo 6: Derivada de una Función Exponencial
- Función:
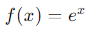
Paso a Paso:
La derivada de 𝑒𝑥 es 𝑒𝑥.
Explicación:
Las funciones exponenciales aparecen en el análisis de circuitos cuando tratamos con el crecimiento o decaimiento de voltajes y corrientes en los circuitos RC y RL. La propiedad única de 𝑒𝑥 es que su derivada es igual a la función misma.
Ejemplo 7: Derivada de una Función Logarítmica
- Función:
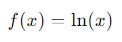
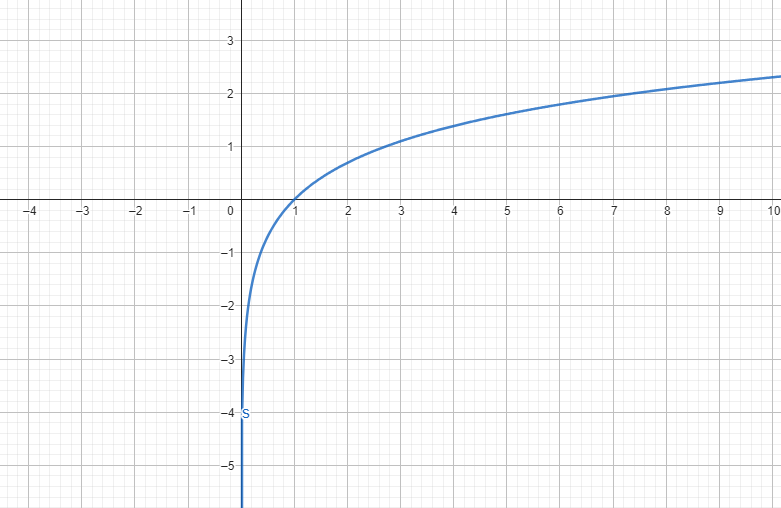
Paso a Paso:
- La derivada de ln(𝑥) es:
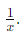
Derivada:
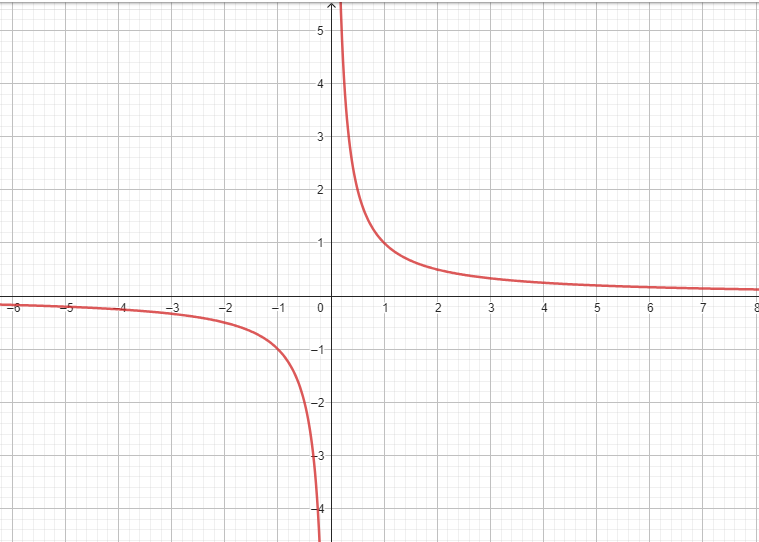
Explicación:
Las funciones logarítmicas son útiles para describir la respuesta en frecuencia de los circuitos y en el análisis de amplificadores logarítmicos. La derivada de ln(𝑥) es crucial para entender la tasa de cambio relativa.
Ejemplo 8: Derivada de una Función Producto
- Función:
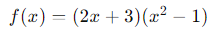
Paso a Paso:
- Aplicamos la regla del producto: (𝑢𝑣)′=𝑢′𝑣+𝑢𝑣′
- Derivamos: 𝑢 = 2𝑥 + 3 y obtenemos 𝑢′ = 2.
- Derivamos:
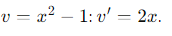
- Sustituimos en la regla:
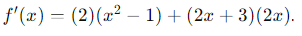
Derivada:
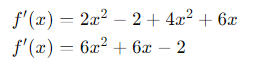
Explicación:
La regla del producto es esencial cuando trabajamos con la multiplicación de dos funciones, algo común en la modelación de señales y en la teoría de control.
Ejemplo 9: Derivada de una Función Cociente
- Función:
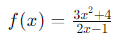
Paso a Paso:
- Aplicamos la regla del cociente:
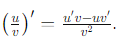
- Derivamos
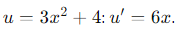
- Derivamos
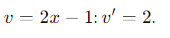
- Sustituimos en la regla:
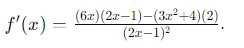
Derivada: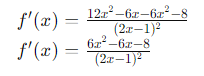
Explicación:
La regla del cociente es crucial cuando se trabaja con la división de funciones, algo que se encuentra frecuentemente en la transferencia de funciones de sistemas y en la respuesta de filtros.
Ejemplo 10: Derivada de una Composición de Funciones
- Función:
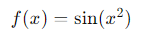
Paso a Paso:
- Aplicamos la regla de la cadena:
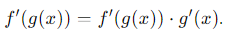
- Derivamos la función exterior:
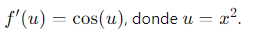
- Derivamos la función interior:
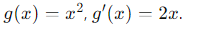
- Multiplicamos las derivadas:
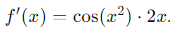
Derivada: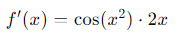
Explicación:
La regla de la cadena es fundamental cuando se trabaja con funciones compuestas, algo común en la transformación de señales y en la modulación de amplitud.
📢 ¡Gracias por leer! Mantente conectado para más contenido educativo 📚
Espero que este post te haya sido útil. Si fue así, no olvides dejar un comentario y compartir tus pensamientos o preguntas. 📝
🔔 No te pierdas mis próximas publicaciones, donde seguiremos explorando el fascinante mundo de la electrónica y los circuitos. Cada semana traeré nuevos temas, ejemplos prácticos y recursos para que sigas aprendiendo y mejorando tus habilidades.
🤝 Sígueme en mis redes sociales, donde podrás conectarte con otros entusiastas de la electrónica, hacer preguntas y recibir ayuda en tiempo real. ¡Estamos aquí para ayudarte!
📷 Comparte tus Proyectos: Si has aplicado estos conocimientos en tus propios proyectos, ¡nos encantaría verlos! Comparte tus avances y aprende de otros en nuestra comunidad.
🌟 Mantente en Contacto: Sígueme en mis redes sociales para actualizaciones, contenido exclusivo y más consejos sobre electrónica y circuitos. Tu participación y apoyo son lo que hace que esta comunidad crezca y se enriquezca.
¡Nos estamos leyendo! Hasta entonces, sigue explorando, aprendiendo y compartiendo. ¡Juntos, hacemos la electrónica más accesible y emocionante para todos! 🚀✨
[ENG]
Hello beautiful Hive community! 👋
Today we will continue immersing ourselves in the fascinating world of derivatives. 🧠🔍 This knowledge is crucial to understanding and solving complex problems, including solving electrical circuits in future lessons. 🚀⚡
Continuing our journey through the fascinating world of derivatives
I want to share with you 10 practical solved examples. These exercises will not only reinforce your knowledge, but will also show you how to apply derivatives to electronics problems. 📐⚡ Derivatives are a powerful tool in circuit analysis and design, especially when we deal with time-varying signals. Let's dive into these examples!
Example 1: Derivative of a Linear Function
- Function:
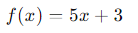

Step by Step:
- 1. We identify the terms of the function: 5𝑥 and 3.
- 2. The derivative of a constant (3) is 0.
- 3. The derivative of 5𝑥 is 5 (coefficient of 𝑥).
- 4. We add the derivatives.
Derived:
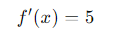

Explanation:
The derivative of a linear function is simply the slope of the line. In this case, the slope is 5, which means that for every unit we increase in 𝑥, 𝑓(𝑥) increases by 5 units.
Example 2: Derivative of a Quadratic Function
- Function:
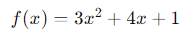

Step by Step:
- 1. We differentiate 3𝑥2: we lower the exponent and multiply by the coefficient: 2⋅3𝑥2−1 = 6𝑥.
- 2. We differentiate 4𝑥: the coefficient is the derivative (4).
- 3. The derivative of a constant (1) is 0.
- 4. We add the derivatives.
Derived:
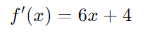

Explanation:
The derivative of a quadratic function is a linear function. This gives us the slope of the tangent to the curve at any point 𝑥, indicating how the function changes as we move 𝑥.
Example 3: Derivative of a Cubic Function
- Function:
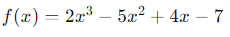

Step by Step:
1. We derive:
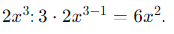
2. We derive:
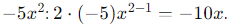
3. We differentiate 4𝑥: the coefficient is the derivative (4).
4. The derivative of a constant (-7) is 0.
5. We add the derivatives.
Derived:
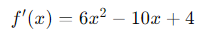

Explanation:
The derivative of a cubic function is a quadratic function, which shows us how the rate of change of the function is not constant, but varies nonlinearly as we move 𝑥.
Example 4: Derivative of a Trigonometric Function (Sine)
- Function:
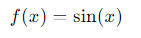

Step by Step:
The derivative of sin(𝑥) is cos(𝑥).
- Derived:
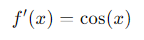

Explanation:
In electronics, the sine and cosine functions are essential for describing alternating current (AC) signals. Knowing how to derive these functions is crucial to understanding how these signals vary over time. To learn more about this, I invite you to see my post dedicated to [alternating current](https://hive.blog/electronic/@profwhitetower/esp-eng-parte-5-or-introduction-to-kirchhoff-s -laws-fundamentals-of-circuit-analysis-part-4)
Example 5: Derivative of a Trigonometric Function (Cosine)
- Function:
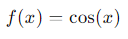
Step by Step:
- 1. The derivative of cos (𝑥) is −sin(𝑥).
Derived: 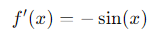

Explanation:
The derivative of the cosine is the negative of the sine, reflecting how the slope of the cosine function changes at each point. This is useful when we analyze the phase of signals in a circuit.
Example 6: Derivative of an Exponential Function
- Function:
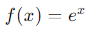

Step by Step:
The derivative of 𝑒𝑥 is 𝑒𝑥.
Explanation:
Exponential functions appear in circuit analysis when we deal with the growth or decay of voltages and currents in RC and RL circuits. The unique property of 𝑒𝑥 is that its derivative is equal to the function itself.
Example 7: Derivative of a Logarithmic Function
- Function:
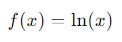

Step by Step:
- The derivative of ln(𝑥) is:
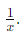
Derived:

Explanation:
Logarithmic functions are useful in describing the frequency response of circuits and in the analysis of logarithmic amplifiers. The derivative of ln(𝑥) is crucial to understanding the relative rate of change.
Example 8: Derivative of a Product Function
- Function:
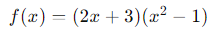
Step by Step:
- We apply the product rule: (𝑢𝑣)′=𝑢′𝑣+𝑢𝑣′
- We differentiate: 𝑢 = 2𝑥 + 3 and we obtain 𝑢′ = 2.
- We derive:
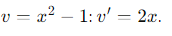
- We substitute in the rule:
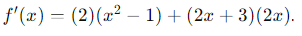
Derived:
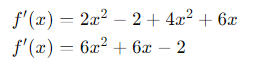
Explanation:
The product rule is essential when we work with the multiplication of two functions, something common in signal modeling and control theory.
Example 9: Derivative of a Quotient Function
- Function:
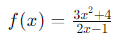
Step by Step:
- We apply the quotient rule:
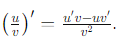
- We derive
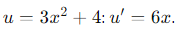
- We derive
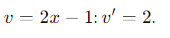
- We substitute in the rule:
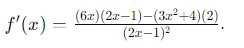
Derived: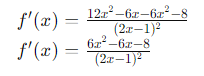
Explanation:
The quotient rule is crucial when working with division of functions, something frequently encountered in system function transfer and filter response.
Example 10: Derivative of a Composition of Functions
- Function:
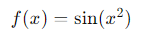
Step by Step:
- We apply the chain rule:
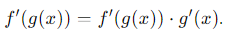
- We derive the outer function:
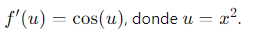
- We derive the inner function:
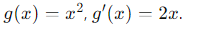
- We multiply the derivatives:
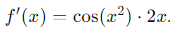
Derived: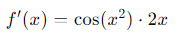
Explanation:
The chain rule is essential when working with composite functions, something common in signal transformation and amplitude modulation.
📢 Thanks for reading! Stay tuned for more educational content 📚
I hope this post has been useful to you. If so, don't forget to leave a comment and share your thoughts or questions. 📝
🔔 Don't miss my next posts, where we will continue exploring the fascinating world of electronics and circuits. Each week I will bring new topics, practical examples and resources so that you continue learning and improving your skills.
🤝 Follow me on my social networks, where you can connect with other electronics enthusiasts, ask questions and receive help in real time. We are here to help you!
📷 Share your Projects: If you have applied this knowledge in your own projects, we would love to see them! Share your progress and learn from others in our community.
🌟 Stay in Touch: Follow me on my social networks for updates, exclusive content and more tips on electronics and circuits. Your participation and support are what make this community grow and enrich.
We are reading each other! Until then, keep exploring, learning and sharing. Together, we make electronics more accessible and exciting for everyone! 🚀✨
Congratulations @profwhitetower! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 2750 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts: